Câu hỏi:
14/12/2024 22364 là lũy thừa của số tự nhiên nào và có số mũ bằng bao nhiêu?
A. Lũy thừa của cơ số 3 và số mũ bằng 5;
B. Lũy thừa của cơ số 2 và số mũ bằng 6;
C. Lũy thừa của cơ số 3 và số mũ bằng 4;
D. Lũy thừa của cơ số 2 và số mũ bằng 5.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: B.
Lời giải
Ta có:
Lũy thừa của cơ số 3 và số mũ bằng 5 là:
35 = 3 . 3 . 3 . 3 . 3 = 243;
Lũy thừa của 2 và số mũ bằng 6 là:
26 = 2 . 2 . 2 . 2 . 2 . 2 = 64;
Lũy thừa của 3 và số mũ bằng 4 là:
34 = 3 . 3 . 3 . 3 = 81;
Lũy thừa của 2 và số mũ bằng 5 là:
25 = 2 . 2 . 2 . 2 . 2 = 32.
Vậy 64 là lũy thừa của cơ số là 2 và số mũ bằng 6.
*Phương pháp giải:
Luỹ thừa bậc n của một số hữu tỉ x, kí hiệu xn , là tích của n thừa số x.
xn = (x ∈ ℚ, n ∈ ℕ, n >1).
– Ta đọc xn là “x mũ n” hoặc “x luỹ thừa n” hoặc “luỹ thừa bậc n của x”.
– Số x được gọi là cơ số, n gọi là số mũ.
*Lý thuyết:
1. Luỹ thừa với số mũ tự nhiên
– Luỹ thừa bậc n của một số hữu tỉ x, kí hiệu xn , là tích của n thừa số x.
xn = (x ∈ ℚ, n ∈ ℕ, n >1).
– Ta đọc xn là “x mũ n” hoặc “x luỹ thừa n” hoặc “luỹ thừa bậc n của x”.
– Số x được gọi là cơ số, n gọi là số mũ.
– Quy ước:
• x1 = x;
• x0 = 1 (x ≠ 0).
– Chú ý:
Khi viết số hữu tỉ x dưới dạng (a, b ∈ ℤ, b ≠ 0) ta có:
Vậy
2. Tích và thương của hai luỹ thừa cùng cơ số
– Khi nhân hai luỹ thừa cùng cơ số, ta giữ nguyên cơ số và cộng hai số mũ.
xm . xn = xm+n
– Khi chia hai luỹ thừa cùng cơ số khác 0, ta giữ nguyên cơ số và lấy số mũ của luỹ thừa bị chia trừ đi số mũ của luỹ thừa chia.
xm : xn = xm – n (x ¹ 0, m ³ n)
Xem thêm
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Trong chân không, vận tốc ánh sáng là 299 792 458 m/s; với các tính toán không cần độ chính xác cao ta có thể coi vận tốc ánh sáng là 3.108 m/s. Trong một nghiên cứu, ánh sáng từ một ngôi sao đến Trái Đất mất 10 phút 20 giây. Khoảng cách giữa ngôi sao đó đến Trái Đất xấp xỉ bằng bao nhiêu ki-lô-mét?
Câu 2:
Trong đợt tri ân khách hàng của một cửa hàng điện máy xanh, cửa hàng giảm 20% giá niêm yết cho mỗi một sản phẩm tivi LG. Cửa hàng vẫn lãi 10% của giá nhập về đối với mỗi chiếc tivi bán ra. Giá niêm yết của một chiếc tivi là bao nhiêu, biết rằng mỗi sản phẩm tivi bán ra thì cửa hàng lãi được 800 000 đồng.
Câu 3:
Lan mang một số tiền dự định mua 4 quyển vở về viết. Do có đợt giảm giác nên với cùng số tiền đó Lan đã mua được 5 quyển vở với giá đã giảm là 12 000 đồng mỗi quyển. Giá tiền ban đầu khi chưa giảm giá của mỗi quyển vở là:
Câu 4:
Lan muốn mua một chiếc áo nhưng không biết chiều dài của áo tương ứng với các size S, M, L. Người bán hàng cho biết chiều dài áo tương ứng với các size S, M, L lần lượt là 48,5 cm; 50,2 cm; 52,4 cm. Chiếc áo Lan mua phải dài hơn \(\frac{1}{3}\) chiều cao của Lan, biết Lan cao 155 cm. Lan nên mua chiếc áo có size gì?
Câu 5:
Dưới đây là biểu đồ biểu chiều cao trung bình của nam và nữ ở một số quốc gia châu Á:
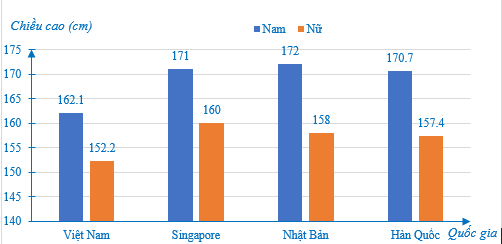
Sự chênh lệch chiều cao giữa nam và nữ ở nước nào lớn nhất?
Câu 6:
Một ô tô đi từ A đến B với vận tốc 50,5 km/giờ mất 1 giờ 30 phút. Một chiếc xe máy đi với vận tốc bằng \(\frac{5}{6}\) vận tốc của ô tô thì sau bao lâu sẽ đi hết quãng đường AB?
Câu 9:
Kết luận nào đúng về giá trị của biểu thức \({\rm{A = }}\frac{1}{5}{\rm{ }} - {\rm{ }}\left[ {\left( {\frac{{ - {\rm{ 2}}}}{3}} \right){\rm{ }} - {\rm{ }}\left( {\frac{1}{3}{\rm{ + }}\frac{5}{6}} \right)} \right]?\)
Câu 10:
Khi bỏ dấu ngoặc trong biểu thức − (− a + b − 5 − c) ta được kết quả là:
Câu 12:
Trong các phép tính của số hữu tỉ, thứ tự thực hiện phép tính đối với biểu thức không có dấu ngoặc là:
Câu 13:
Anh Minh kinh doanh hoa quả nhập khẩu. Trong lần nhập hàng vừa qua anh đã bỏ ra 90 000 000 đồng để nhập lô hàng mới. Nhưng do quá trình vận chuyển không được đảm bảo nên \(\frac{1}{3}\) số hàng nhập về không đảm bảo chất lượng. Anh Minh đã bán số hàng còn lại cao hơn 10% so với giá nhập vào và số hàng không đảm bảo chất lượng thấp hơn 15% so với giá nhập vào. Hỏi doanh thu lô hàng mới của anh Minh là bao nhiêu?
Câu 14:
Cho hai biểu thức sau, khẳng định nào sau đây đúng?
\(A{\rm{ = }}\frac{{11}}{2}{\rm{ }}{\rm{. 0,62 : }}\left( {\frac{{ - {\rm{ 3}}}}{{100}}} \right);\)\(B{\rm{ = }}\frac{{12}}{{ - {\rm{ 5}}}}{\rm{ : }}\frac{8}{{45}}{\rm{ }}{\rm{. }}\frac{9}{{10}}.\)


