Ba bạn Hạnh, Nguyên, Trang đi đến trường theo ba con đường AD, BD, và CD

Giải Toán 7 Luyện tập trang 56

Video giải Bài 5 trang 56 Toán lớp 7 Tập 2

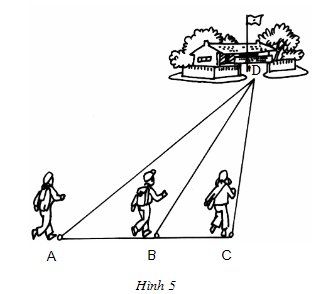
Bài 5 trang 56 Toán lớp 7 Tập 2: Ba bạn Hạnh, Nguyên, Trang đi đến trường theo ba con đường AD, BD, và CD (h.5). Biết rằng ba điểm A, B, C cùng nằm trên một đường thẳng và góc ACD là góc tù.

Hỏi ai đi xa nhất, ai đi gần nhất? Hãy giải thích.

Lời giải

+ Trong ∆BCD có góc C là góc tù (giả thiết) nên góc C lớn nhất suy ra BD lớn nhất (vì BD là cạnh đối diện với góc C). Do đó BD > CD (1).

+ $\widehat{ABD}$ là góc ngoài tại đỉnh B của tam giác BCD. Ta có: $\widehat{ABD}=\widehat{C}+\widehat{BDC}\Rightarrow \widehat{ABD}>\widehat{C}$.

Mà $\widehat{C}>90°\Rightarrow \widehat{ABD}>90°.$ Do đó $\widehat{ABD}$ cũng là góc tù.

Trong ∆ABD có góc B là góc tù (chứng minh trên) nên góc B lớn nhất suy ra AD lớn nhất (vì AD là cạnh đối diện với góc B). Do đó AD > BD (2).

Từ (1) và (2) suy ra AD > BD > CD.

Vậy Hạnh đi xa nhất, Trang đi gần nhất.

Xem thêm lời giải bài tập Toán lớp 7 hay, chi tiết khác:

Bài 3 trang 56 Toán 7 Tập 2: Cho tam giác ABC với $\hat{A}=100°; \hat{B}=40°$. a) Tìm cạnh lớn nhất của tam giác ABC...

Bài 4 trang 56 Toán 7 Tập 2: Trong một tam giác, đối diện với cạnh nhỏ nhất là góc gì (nhọn, vuông, tù)? Tại sao?...

Bài 6 trang 56 Toán 7 Tập 2: Xem hình 6, có hai đoạn bằng nhau BC và DC. Hỏi rằng kết luận nào trong các kết luận sau là đúng? Tại sao?...

Bài 7 trang 56 Toán 7 Tập 2: Một cách chứng minh khác của định lí 1...