Nội dung bài viết

    Xem thêm

    Từ một điểm M cố định ở bên ngoài đường tròn (O)

    Với giải câu hỏi 25 trang 104 sbt Toán lớp 9 Tập 2 được biên soạn lời giải chi tiết sẽ giúp học sinh biết cách làm bài tập môn Toán 9. Mời các bạn đón xem:

    1 987 29/03/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Giải SBT Toán 9 Bài 4: Góc tạo bởi tia tiếp tuyến và dây cung

    Bài 25 trang 104 SBT Toán 9 Tập 2: Từ một điểm M cố định ở bên ngoài đường tròn (O), kẻ một tiếp tuyến MT và một cát tuyến MAB của đường tròn đó.

    a) Chứng minh rằng luôn có MT2 = MA.MB và tích này không phụ thuộc vị trí của cát tuyến MAB.

    b) Ở hình 2 khi cho MT = 20cm, MB = 50cm, tính bán kính đường tròn.

    Lời giải:

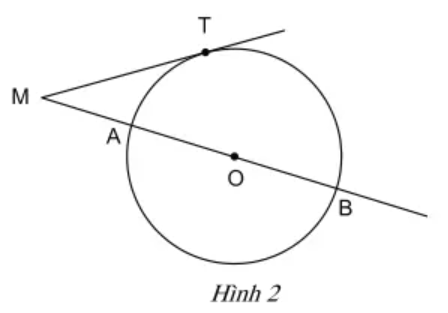
    a)

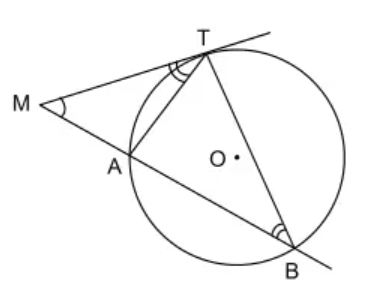
    Xét tam giác MTA và tam giác MTB có:

    Góc M chung

     MTA^=TBA^ (hệ quả góc giữa tia tiếp tuyến và dây)

    Hay MTA^=TBM^

    Do đó, tam giác MAT đồng dạng với tam giác MTB (góc – góc)

    ⇒MTMA=MBMT

    ⇒MT2=MA.MB

    Vì MA.MB=MT2  và MT là tiếp tuyến của đường tròn (O) nên tích MA.MB không phụ thuộc vị trí của cát tuyến MAB.

    b)

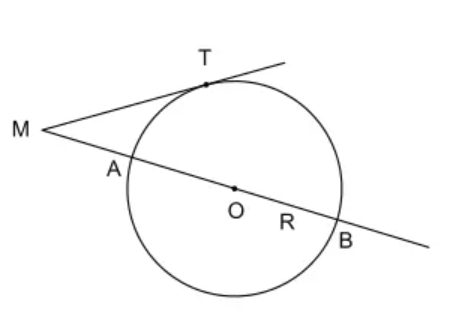
    Gọi bán kính đường tròn (O) là R

    MB = MA + AB = MA + 2R

     MT2=MA.MB(chứng minh trên)

    ⇒MT2=MB−2R.MB

     ⇒R=MB2−MT22MB=502−2022.50=21(cm).

    Xem thêm lời giải sách bài tập Toán lớp 9 hay, chi tiết khác:

    Câu hỏi 24 trang 103 SBT Toán 9 Tập 2: Hai đường tròn (O) và (O’) cắt nhau tại A...

    Câu hỏi 26 trang 104 SBT Toán 9 Tập 2: Ngồi trên đỉnh núi cao 1 km thì có thể...

    Câu hỏi 27 trang 104 SBT Toán 9 Tập 2: Cho tam giác ABC nội tiếp trong đường...

    Bài tập bổ sung

    Câu hỏi 4.1 trang 104 SBT Toán 9 Tập 2: Cho đường tròn tâm O bán kính R...

    Câu hỏi 4.2 trang 104 SBT Toán 9 Tập 2: Cho tam giác ABC vuông ở A,...

    Tham khảo các loạt bài Toán 9 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 987 29/03/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: