Nội dung bài viết

    Xem thêm

    Cho tam giác ABC vuông ở A, AH và AM tương ứng

    Với giải câu hỏi 4.2 trang 104 sbt Toán lớp 9 Tập 2 được biên soạn lời giải chi tiết sẽ giúp học sinh biết cách làm bài tập môn Toán 9. Mời các bạn đón xem:

    1 469 29/03/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Giải SBT Toán 9 Bài 4: Góc tạo bởi tia tiếp tuyến và dây cung

    Bài 4.2 trang 104 SBT Toán 9 Tập 2: Cho tam giác ABC vuông ở A, AH và AM tương ứng là đường cao và đường trung tuyến kẻ từ A của tam giác đó. Qua điểm A kẻ đường thẳng mn vuông góc với AM. Chứng minh: AB và AC tương ứng là tia phân giác của các góc tạo bởi AH và hai tia Am, An của đường thẳng mn.

    Lời giải:

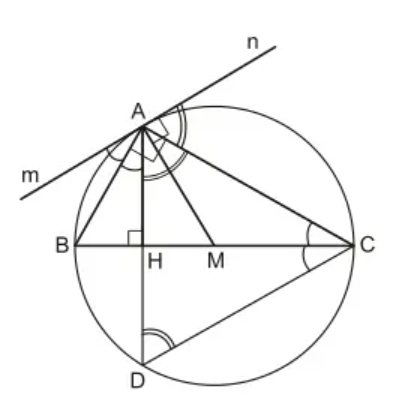
    Vì tam giác ABC vuông tại A, có AM là đường trung tuyến ứng với cạnh huyền BC

     ⇒AM=MB=MC=12BC (tính chất đường trung tuyến trong tam giác vuông)

    Nên đường tròn tâm M bán kính MA đi qua A, B, C

    Gọi D là giao điểm của AH với đường tròn (M; MA)

    Khi đó: BC vuông góc với AD tại H nên H là trung điểm của AD (quan hệ giữa đường kính và dây của đường tròn)

    Do đó, BC là đường trung trực của AD

    ⇒ AC = CD (tính chất đường trung trực của đoạn thẳng)

    Do đó, tam giác ACD cân tại C

     ⇒ADC^=DAC^ (1)

    Ta lại có:  ADC^=nAC^ (hệ quả của góc giữa tia tiếp tuyến và dây cung) (2)

    Từ (1) và (2) ta suy ra: DAC^=nAC^  hay HAC^=nAC^

    Vậy AC là tia phân giác của HAn^ .

    Ta có:  ACB^=mAB^ (hệ quả của góc giữa tia tiếp tuyến và dây cung) (3)

     BAH^=ACB^ (cùng phụ với góc HAC) (4)

    Từ (3), (4) ta suy ra: mAB^=BAH^

    Vậy AB là tia phân giác của mAH^ .

    Xem thêm lời giải sách bài tập Toán lớp 9 hay, chi tiết khác:

    Câu hỏi 24 trang 103 SBT Toán 9 Tập 2: Hai đường tròn (O) và (O’) cắt nhau tại A...

    Câu hỏi 25 trang 104 SBT Toán 9 Tập 2: Từ một điểm M cố định ở bên ngoài...

    Câu hỏi 26 trang 104 SBT Toán 9 Tập 2: Ngồi trên đỉnh núi cao 1 km thì có thể...

    Câu hỏi 27 trang 104 SBT Toán 9 Tập 2: Cho tam giác ABC nội tiếp trong đường...

    Bài tập bổ sung

    Câu hỏi 4.1 trang 104 SBT Toán 9 Tập 2: Cho đường tròn tâm O bán kính R...

    Tham khảo các loạt bài Toán 9 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 469 29/03/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: