Toán 12 Bài 2 (Cánh diều): Công thức xác suất toàn phần. Công thức Bayes

Giải Toán 12 Bài 2: Công thức xác suất toàn phần. Công thức Bayes

Câu hỏi khởi động trang 97 Toán 12 Tập 2: Dây chuyền lắp ráp ô tô điện gồm các linh kiện là sản phẩm do hai nhà máy sản xuất ra. Số linh kiện nhà máy I sản xuất ra chiếm 55% tổng số linh kiện, số linh kiện nhà máy II sản xuất ra chiếm 45% tổng số linh kiện; tỉ lệ linh kiện đạt tiêu chuẩn của nhà máy I là 90%, của nhà máy II là 87%. Lấy ngẫu nhiên ra một linh kiện từ dây chuyền lắp ráp đó để kiểm tra.

Xác suất để linh kiện được lấy ra đạt tiêu chuẩn là bao nhiêu?

Lời giải:

Sau bài học này, ta giải quyết được bài toán trên như sau:

Xét hai biến cố sau:

A: “Linh kiện được chọn ra đạt tiêu chuẩn”;

B: “Linh kiện được chọn ra do nhà máy I sản xuất”.

Khi đó, ta có:

P(B) = 0,55; P( $\overline{B}$) = 1 – P(B) = 1 – 0,55 = 0,45;

P(A | B) = 0,9; P(A | $\overline{B}$ ) = 0,87.

Áp dụng công thức xác suất toàn phần, ta có:

P(A) = P(B) ∙ P(A | B) + P($\overline{B}$ ) ∙ P(A | $\overline{B}$ ) = 0,55 ∙ 0,9 + 0,45 ∙ 0,87 = 0,8865.

Vậy xác suất để linh kiện được lấy ra đạt tiêu chuẩn bằng 0,8865.

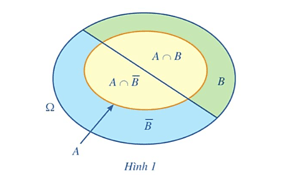
Hoạt động 1 trang 97 Toán 12 Tập 2: Một hộp có 24 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, …, 24; hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên 1 chiếc thẻ trong hộp. Xét biết cố A: “Số xuất hiện trên thẻ được rút ra là số chia hết cho 3” và biến cố B: “Số xuất hiện trên thẻ được rút ra là số chia hết cho 4”.

a) Viết các tập con của không gian mẫu tương ứng với các biến cố A, B, A ∩ B, $A\cap \overline{B}$ (Hình 1).

Từ đó, hãy chứng tỏ rằng: P(A) = P(A ∩ B) + P($A\cap \overline{B}$ ).

c) So sánh: P(A ∩ B) và P(B) ∙ P(A | B);

P( $A\cap \overline{B}$) và P($\overline{B}$ ) ∙ P(A | $\overline{B}$ ).

Từ đó, hãy chứng tỏ rằng: P(A) = P(B) ∙ P(A | B) + P( $\overline{B}$) ∙ P(A | $\overline{B}$ ).

Lời giải:

a) Ω = {1; 2; 3; …; 24}.

A = {3; 6; 9; 12; 15; 18; 21; 24}.

B = {4; 8; 12; 16; 20; 24}.

A ∩ B = {12; 24}.

$\overline{B}$ = {1; 2; 3; 5; 6; 7; 9; 10; 11; 13; 14; 15; 17; 18; 19; 21; 22; 23}.

A ∩ $\overline{B}$ = {3; 6; 9; 15; 18; 21}.

b) Từ câu a), suy ra n(A) = 8, n(A ∩ B) = 2, n(A ∩ $\overline{B}$ ) = 6.

Do 8 = 2 + 6 nên n(A) = n(A ∩ B) + n( $A\cap \overline{B}$).

Khi đó, P(A) = $\frac{n\left(A\right)}{n\left(\Omega \right)}$ = $\frac{n\left(A\cap B\right)+n\left(A\cap \overline{B}\right)}{n\left(\Omega \right)}$ = $\frac{n\left(A\cap B\right)}{n\left(\Omega \right)}$ + $\frac{n\left(A\cap \overline{B}\right)}{n\left(\Omega \right)}$ .

Mà P(A ∩ B) = $\frac{n\left(A\cap B\right)}{n\left(\Omega \right)}$ ; P($A\cap \overline{B}$ ) = $\frac{n\left(A\cap \overline{B}\right)}{n\left(\Omega \right)}$ .

Vậy P(A) = P(A ∩ B) + P( $A\cap \overline{B}$).

c) Ta có P(B) ∙ P(A | B) = P(B) ∙ $\frac{P\left(A\cap B\right)}{P\left(B\right)}$ = P(A ∩ B).

P( $\overline{B}$) ∙ P(A | $\overline{B}$ ) = P( $\overline{B}$) ∙ $\frac{P\left(A\cap \overline{B}\right)}{P\left(\overline{B}\right)}$ = P( $A\cap \overline{B}$).

Vì hai biến cố A ∩ B và $A\cap \overline{B}$ là hai biến cố xung khắc và (A ∩ B) ∪ ($A\cap \overline{B}$ ) = A nên theo công thức xác suất ta có

P(A) = P(A ∩ B) + P($A\cap \overline{B}$ ) = P(B) ∙ P(A | B) + P( $\overline{B}$) ∙ P(A | $\overline{B}$ ).

Luyện tập 1 trang 99 Toán 12 Tập 2: Hãy giải bài toán trong phần mở đầu bằng cách lập bảng thống kê như trong Ví dụ 2, biết rằng cả hai nhà máy sản xuất được 10 000 linh kiện.

Lời giải:

Số linh kiện nhà máy I sản xuất ra là: 55% ∙ 10 000 = 5 500 (linh kiện).

Số linh kiện nhà máy II sản xuất ra là: 45% ∙ 10 000 = 4 500 (linh kiện).

Số linh kiện nhà máy I sản xuất ra đạt tiêu chuẩn là: 90% ∙ 5 500 = 4 950 (linh kiện), không đạt tiêu chuẩn là: 5 500 – 4 950 = 550 (linh kiện).

Số linh kiện nhà máy II sản xuất ra đạt tiêu chuẩn là: 87% ∙ 4 500 = 3 915 (linh kiện), không đạt tiêu chuẩn là: 4 500 – 3 915 = 585 (linh kiện).

Từ đó ta có bảng thống kê như sau (đơn vị: linh kiện)

Tiêu chuẩn Linh kiện	Đạt tiêu chuẩn	Không đạt tiêu chuẩn
Nhà máy I sản xuất	4 950	550
Nhà máy II sản xuất	3 915	585

Xét hai biến cố sau:

A: “Linh kiện được chọn ra đạt tiêu chuẩn”;

B: “Linh kiện được chọn ra do nhà máy I sản xuất”.

Khi đó, ta có:

P(B) = 0,55; P($\overline{B}$ ) = 1 – P(B) = 1 – 0,55 = 0,45; P(A | B) = 0,9; P(A | $\overline{B}$ ) = 0,87.

Áp dụng công thức xác suất toàn phần, ta có:

P(A) = P(B) ∙ P(A | B) + P( $\overline{B}$) ∙ P(A | $\overline{B}$ ) = 0,55 ∙ 0,9 + 0,45 ∙ 0,87 = 0,8865.

Vậy xác suất để linh kiện được lấy ra đạt tiêu chuẩn bằng 0,8865.

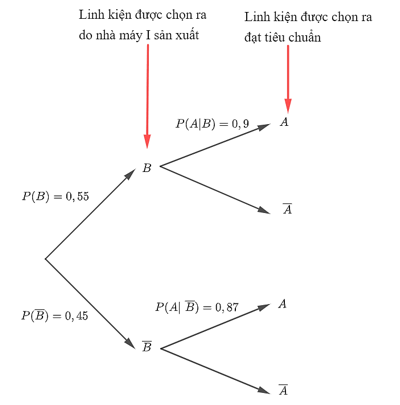
Luyện tập 2 trang 100 Toán 12 Tập 2: Hãy giải bài toán trong phần mở đầu bằng phương pháp sử dụng sơ đồ hình cây như trong Ví dụ 3.

Lời giải:

Xét hai biến cố sau:

A: “Linh kiện được chọn ra đạt tiêu chuẩn”;

B: “Linh kiện được chọn ra do nhà máy I sản xuất”.

Khi đó, ta có:

P(B) = 0,55; P($\overline{B}$ ) = 1 – P(B) = 1 – 0,55 = 0,45; P(A | B) = 0,9; P(A | $\overline{B}$ ) = 0,87.

Sơ đồ hình cây biểu thị tình huống đã cho là:

Áp dụng công thức xác suất toàn phần, ta có:

P(A) = P(B) ∙ P(A | B) + P( $\overline{B}$) ∙ P(A | $\overline{B}$ ) = 0,55 ∙ 0,9 + 0,45 ∙ 0,87 = 0,8865.

Vậy xác suất để linh kiện được lấy ra đạt tiêu chuẩn bằng 0,8865.

Hoạt động 2 trang 100 Toán 12 Tập 2: Xét hai biến cố A, B trong Hoạt động 1.

a) Tính: P(A), P(B), P(A | B) và P(B | A).

b) So sánh: P(B | A) và $\frac{P\left(B\right)\cdot P\left(A|B\right)}{P\left(A\right)}$

Lời giải:

a) Ta có: P(A) = $\frac{n\left(A\right)}{n\left(\Omega \right)}$ = $\frac{8}{24}=\frac{1}{3}$ ; P(B) = $\frac{n\left(B\right)}{n\left(\Omega \right)}$ = $\frac{6}{24}=\frac{1}{4}$ ;

P(A | B) = $\frac{n\left(A\cap B\right)}{n\left(B\right)}=\frac{2}{6}=\frac{1}{3}$ ; P(B | A) = $\frac{n\left(A\cap B\right)}{n\left(A\right)}=\frac{2}{8}=\frac{1}{4}$ .

b) Ta có: $\frac{P\left(B\right)\cdot P\left(A|B\right)}{P\left(A\right)}=\frac{\frac{1}{4}\cdot \frac{1}{3}}{\frac{1}{3}}=\frac{1}{4}$= P(B | A).

Luyện tập 3 trang 101 Toán 12 Tập 2: Cho hai biến cố A, B sao cho P(A) = 0,4; P(B) = 0,8; P(B | A) = 0,3. Tính P(A | B).

Lời giải:

Áp dụng công thức Bayes, ta có:

P(A | B) = $\frac{P\left(A\right)\cdot P\left(B|A\right)}{P\left(B\right)}=\frac{0,4\cdot 0,3}{0,8}=0,15$

Luyện tập 4 trang 101 Toán 12 Tập 2: Được biết có 5% đàn ông bị mù màu, và 0,25% phụ nữ bị mù màu (Nguồn: F. M. Dekking et al., A modern introduction to probability and statistics – Understanding why and how, Springer, 2005). Giả sử số đàn ông bằng số phụ nữ. Chọn một người bị mù màu một cách ngẫu nhiên. Hỏi xác suất để người đó là đàn ông là bao nhiêu?

Lời giải:

Xét hai biến cố:

A: “Người được chọn là đàn ông”;

B: “Người được chọn bị mù màu”.

Theo bài ra ta có: P(B | A) = 0,05; P(B | $\overline{A}$) = 0,0025.

Vì số đàn ông bằng số phụ nữ nên ta có P(A) = 0,5 và P($\overline{A}$ ) = 1 – 0,5 = 0,5.

Áp dụng công thức Bayes, ta có xác suất để một người mù màu được chọn là đàn ông là: P(A | B) = $\frac{P\left(A\right)\cdot P\left(B|A\right)}{P\left(A\right)\cdot P\left(B|A\right)+P\left(\overline{A}\right)\cdot P\left(B|\overline{A}\right)}=\frac{0,5\cdot 0,05}{0,5\cdot 0,05+0,5\cdot 0,0025}$≈ 0,9524.

Bài tập

Bài 1 trang 102 Toán 12 Tập 2: Cho hai biến cố A, B với P(B) = 0,6; P(A | B) = 0,7 và P(A | $\overline{B}$) = 0,4. Khi đó, P(A) bằng:

A. 0,7.

B. 0,4.

C. 0,58.

D. 0,52.

Lời giải:

Đáp án đúng là: C

Ta có P(B) = 0,6. Suy ra P( $\overline{B}$) = 1 – P(B) = 1 – 0,6 = 0,4.

Áp dụng công thức xác suất toàn phần, ta có:

P(A) = P(B) ∙ P(A | B) + P($\overline{B}$ ) ∙ P(A | $\overline{B}$ ) = 0,6 ∙ 0,7 + 0,4 ∙ 0,4 = 0,58.

Bài 2 trang 102 Toán 12 Tập 2: Có hai chiếc hộp, hộp I có 5 viên bi màu trắng và 5 viên bi màu đen, hộp II có 6 viên bi màu trắng và 4 viên bi màu đen, các viên bi có cùng kích thước và khối lượng. Lấy ngẫu nhiên một viên bi từ hộp I bỏ sang hộp II.

Sau đó lấy ngẫu nhiên một viên bi từ hộp II.

a) Tính xác suất để viên bi được lấy ra từ hộp II là viên bi màu trắng.

b) Giả sử viên bi được lấy ra từ hộp II là viên bi màu trắng. Tính xác suất viên bi màu trắng đó thuộc hộp I.

Lời giải:

a) Xét hai biến cố:

A: “Viên bi được lấy ra từ hộp I bỏ sang hộp II là màu trắng”;

B: “Viên bi được lấy ra từ hộp II là viên bi màu trắng”.

Theo bài ra ta có: P(A) = $\frac{5}{10}=\frac{1}{2}$ ; P( $\overline{A}$) = 1 – P(A) = $\frac{1}{2}$ .

P(B | A) = $\frac{7}{11}$ ; $P\left(B|\overline{A}\right)=\frac{6}{11}$ .

Áp dụng công thức xác suất toàn phần, ta có:

P(B) = P(A) ∙ P(B | A) + P( $\overline{A}$) ∙ P(B | $\overline{A}$ ) = $\frac{1}{2}\cdot \frac{7}{11}+\frac{1}{2}\cdot \frac{6}{11}=\frac{13}{22}$ .

Vậy xác suất để viên bi được lấy ra từ hộp II là viên bi màu trắng là $\frac{13}{22}$ .

b) Nếu viên bi được lấy ra từ hộp II là viên bi màu trắng thì xác suất viên bi màu trắng đó thuộc hộp I là: P(A | B) = $\frac{P\left(A\right)\cdot P\left(B|A\right)}{P\left(B\right)}=\frac{\frac{1}{2}\cdot \frac{7}{11}}{\frac{13}{22}}=\frac{7}{13}$ .

Vậy nếu viên bi được lấy ra từ hộp II là viên bi màu trắng thì xác suất viên bi màu trắng đó thuộc hộp I là $\frac{7}{13}$

Bài 3 trang 102 Toán 12 Tập 2: Một loại linh kiện do hai nhà máy số I, số II cùng sản xuất. Tỉ lệ phế phẩm của các nhà máy I, II lần lượt là: 4%; 3%. Trong một lô linh kiện để lẫn lộn 80 sản phẩm của nhà máy số I và 120 sản phẩm của nhà máy số II. Một khách hàng lấy ngẫu nhiên một linh kiện từ lô hàng đó.

a) Tính xác suất để linh kiện được lấy ra là linh kiện tốt.

b) Giả sử linh kiện được lấy ra là linh kiện phế phẩm. Xác suất linh kiện đó do nhà máy nào sản xuất là cao hơn?

Lời giải:

a) Xét hai biến cố:

A: “Linh kiện được lấy ra từ lô hàng là linh kiện tốt”;

B: “Linh kiện được lấy ra từ lô hàng do nhà máy I sản xuất”.

Vì lô linh kiện để lẫn lộn 80 sản phẩm của nhà máy số I và 120 sản phẩm của nhà máy số II nên P(B) = $\frac{80}{80+120}=0,4$ , suy ra $P\left(\overline{B}\right)=1-0,4=0,6$ .

Vì tỉ lệ phế phẩm của các nhà máy I, II lần lượt là: 4%; 3% nên tỉ lệ thành phẩm (linh kiện tốt) của các nhà máy I, II lần lượt là 96%; 97%.

Do đó P(A | B) = 0,96 và P(A | $\overline{B}$ ) = 0,97.

Áp dụng công thức xác suất toàn phần, ta có xác suất để linh kiện được lấy ra là linh kiện tốt là:

P(A) = P(B) ∙ P(A | B) + P($\overline{B}$ ) ∙ P(A | $\overline{B}$ ) = 0,4 ∙ 0,96 + 0,6 ∙ 0,97 = 0,966.

b) Xét biến cố C: “Linh kiện được lấy ra từ lô hàng là linh kiện phế phẩm”.

Khi đó, ta có C = $\overline{A}$ . Suy ra P(C) = P($\overline{A}$ ) = 1 – P(A) = 1 – 0,966 = 0,034.

Theo bài ra ta có: P(C | B) = 4% = 0,04.

Do đó, nếu linh kiện được lấy ra là linh kiện phế phẩm thì xác suất sản phẩm đó do nhà máy I sản xuất là: P(B | C) = $\frac{P\left(B\right)\cdot P\left(C|B\right)}{P\left(C\right)}=\frac{0,4\cdot 0,04}{0,034}=\frac{8}{17}$ .

Nếu linh kiện được lấy ra là linh kiện phế phẩm thì xác suất sản phẩm đó do nhà máy II sản xuất là: P( $\overline{B}$ | C) = 1 – P(B | C) = $1-\frac{8}{17}=\frac{9}{17}$ .

Vì $\frac{9}{17}>\frac{8}{17}$ nên nếu linh kiện được lấy ra là linh kiện phế phẩm thì xác suất linh kiện đó do nhà máy II sản xuất là cao hơn.

Bài 4 trang 102 Toán 12 Tập 2: Năm 2001, Cộng đồng châu Âu có làm một đợt kiểm tra rất rộng rãi các con bò để phát hiện những con bị bệnh bò điên. Không có xét nghiệm nào cho kết quả chính xác 100%. Một loại xét nghiệm, mà ở đây ta gọi là xét nghiệm A, cho kết quả như sau: Khi con bò bị bệnh bò điên thì xác suất để có phản ứng dương tính trong xét nghiệm A là 70%, còn khi con bò không bị bệnh thì xác suất để có phản ứng dương tính trong xét nghiệm A là 10%. Biết rằng tỉ lệ bò bị mắc bệnh bò điên ở Hà Lan là 13 con trên 1 000 000 con (Nguồn: F. M. Dekking et al., A modern introduction to probability and statistics – Understanding why and how, Springer, 2005). Hỏi khi một con bò ở Hà Lan có phản ứng dương tính với xét nghiệm A thì xác suất để nó bị mắc bệnh bò điên là bao nhiêu?

Lời giải:

Xét hai biến cố:

A: “Con bò được chọn ra không bị mắc bệnh bò điên”.

B: “Con bò được chọn ra có phản ứng dương tính”.

Vì tỉ lệ bò bị mắc bệnh bò điên ở Hà Lan là 13 con trên 1 000 000 con nên tỉ lệ bò mắc bệnh bò điên ở Hà Lan là P($\overline{A}$) = 0,000013.

Suy ra P(A) = 1 – 0,000013 = 0,999987.

Trong số những con bò không bị mắc bệnh thì xác suất để có phản ứng dương tính trong xét nghiệm A là 10%, suy ra P(B | A) = 0,1.

Khi con bò mắc bệnh bò điên thì xác suất để có phản ứng dương tính trong xét nghiệm A là 70% nên P(B | $\overline{A}$ ) = 0,7.

Ta thấy xác suất mắc bệnh bò điên của một con bò ở Hà Lan xét nghiệm có phản ứng dương tính với xét nghiệm A chính là P( $\overline{A}$ | B). Áp dụng công thức Bayes, ta có:

$P\left(\overline{A}|B\right)=\frac{P\left(\overline{A}\right)\cdot P\left(B|\overline{A}\right)}{P\left(\overline{A}\right)\cdot P\left(B|\overline{A}\right)+P\left(A\right)\cdot P\left(B|A\right)}$

$=\frac{0,000013\cdot 0,7}{0,000013\cdot 0,7+0,999987\cdot 0,1}\approx 0,000091$.

Vậy khi một con bò ở Hà Lan có phản ứng dương tính với xét nghiệm A thì xác suất để nó bị mắc bệnh bò điên là 0,000091.