Nội dung bài viết

    Xem thêm

    Tìm hai số u và v trong mỗi trường hợp sau: u + v = 42, uv = 441

    Với giải bài 32 trang 54 sgk Toán lớp 9 Tập 2 được biên soạn lời giải chi tiết sẽ giúp học sinh biết cách làm bài tập môn Toán 9. Mời các bạn đón xem:

    1 885 05/04/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 9 Luyện tập trang 54

    Video Giải Bài 32 trang 54 SGK Toán 9 Tập 2

    Bài 32 trang 54 SGK Toán 9 Tập 2: Tìm hai số u và v trong mỗi trường hợp sau:

    a) u + v = 42, uv = 441

    b) u + v = -42, uv = -400

    c) u – v = 5, uv = 24

    Lời giải

    a) S = 42; P = 441

    ⇒ S2 – 4P = 422 – 4.441 = 0

    ⇒ u và v là hai nghiệm của phương trình: x2 – 42x + 441 = 0

    Có: Δ’ = (-21)2 – 441 = 0

    ⇒ Phương trình có nghiệm kép x1 = x2 = −b2a=−−422=21.

    Vậy u = v = 21.

    b) S = -42; P = -400

    ⇒ S2 – 4P = (-42)2 – 4.(-400) = 3364 > 0

    ⇒ u và v là hai nghiệm của phương trình: x2 + 42x – 400 = 0

    Có Δ’ = 212 – 1.(-400) = 841

    ⇒ Phương trình có hai nghiệm phân biệt:

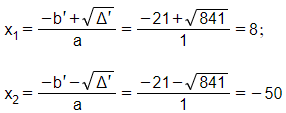
    Tìm hai số u và v trong mỗi trường hợp sau: u + v = 42, uv = 441 (ảnh 1)

    Vậy u = 8; v = -50 hoặc u = -50; v = 8.

    c) u – v = 5 ⇒ u + (-v) = 5

    u.v = 24 ⇒ u.(-v) = -uv = -24.

    Ta tìm u và –v. Từ đó, ta dễ dàng tính được u và v.

    S = u + (-v) = 5; P = u. (-v) = -24

    ⇒ S2 – 4P = 52 – 4.(-24) = 121 > 0

    ⇒ u và –v là hai nghiệm của phương trình: x2 – 5x – 24 = 0

    Có Δ = (-5)2 – 4.1.(-24) = 121

    ⇒ Phương trình có hai nghiệm phân biệt

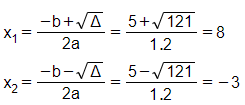
    Tìm hai số u và v trong mỗi trường hợp sau: u + v = 42, uv = 441 (ảnh 1)

    +) Với u = 8 thì –v = -3

    ⇒u=8;v=3

    +) Với u = -3 thì -v = 8

    ⇒u=−3;v=−8.

    Vậy u = 8 thì v = 3 hoặc u = -3 và v = -8

    Xem thêm lời giải bài tập Toán lớp 9 hay, chi tiết khác:

    Bài 29 trang 54 Toán 9 Tập 2: Không giải phương trình, hãy tính tổng và tích các nghiệm (nếu có) của mỗi phương trình...

    Bài 30 trang 54 Toán 9 Tập 2: Tìm giá trị của m để phương trình có nghiệm...

    Bài 31 trang 54 Toán 9 Tập 2: Tính nhẩm nghiệm của các phương trình...

    Bài 33 trang 54 Toán 9 Tập 2: Chứng tỏ rằng nếu phương trình...

    Tham khảo các loạt bài Toán 9 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 885 05/04/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: