Nội dung bài viết

    Xem thêm

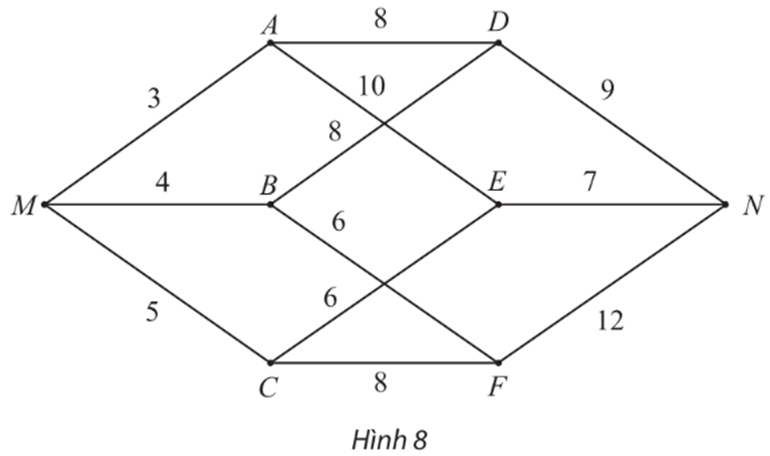
     Tìm đường đi ngắn nhất từ đỉnh M đến N trong đồ thị có trọng số sau

    Lời giải Bài 10 trang 68 Chuyên đề Toán 11 sách Chuyên đề học tập Toán lớp 11 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập.

    1 263 03/07/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Chuyên đề Toán 11 Chân trời sáng tạo Bài tập cuối chuyên đề 2

    Bài 10 trang 68 Chuyên đề Toán 11: Tìm đường đi ngắn nhất từ đỉnh M đến N trong đồ thị có trọng số sau:

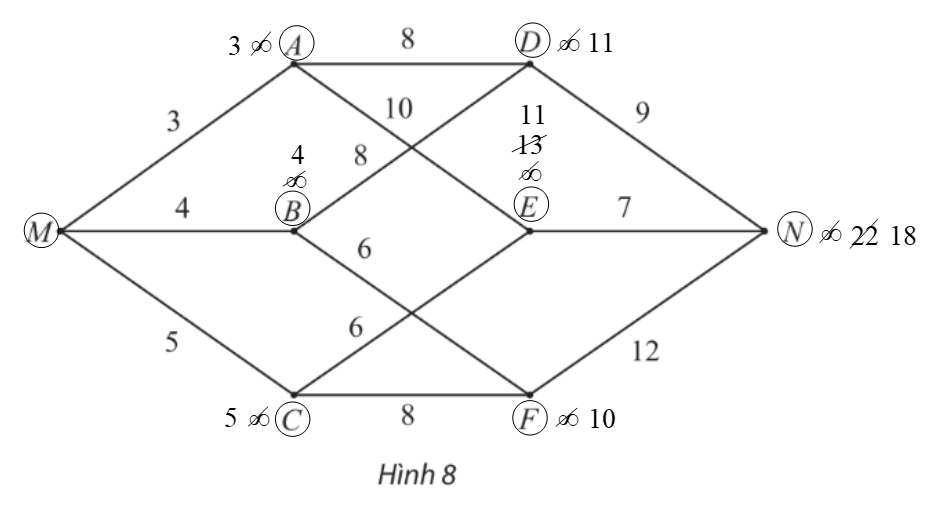
    Bài 10 trang 68 Chuyên đề học tập Toán 11 Chân trời sáng tạo

    Lời giải:

    Bài 10 trang 68 Chuyên đề học tập Toán 11 Chân trời sáng tạo

    – Gán nhãn cho M bằng 0 (tức là, nM = 0), các đỉnh khác bằng ∞. Khoanh tròn đỉnh M.

    – Tại các đỉnh kề với M, gồm A, B, C, ta có:

    ⦁ nA = nM + wMA = 0 + 3 = 3.Vì 3 < ∞ nên ta đổi nhãn của A thành 3.

    ⦁ nB = nM + wMB = 0 + 4 = 4.Vì 4 < ∞ nên ta đổi nhãn của B thành 4.

    ⦁ nC = nM + wMC = 0 + 5 = 5.Vì 5 < ∞ nên ta đổi nhãn của C thành 5.

    Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là A nên ta khoanh tròn đỉnh A (đỉnh gần M nhất, chỉ tính các điểm khác M).

    – Trong các đỉnh chưa được khoanh tròn, đỉnh kề với A gồm D, E, ta có:

    ⦁ nD = nA + wAD = 3 + 8 = 11.Vì 11 < ∞ nên ta đổi nhãn của D thành 11.

    ⦁ nE = nA + wAE = 3 + 10 = 13.Vì 13 < ∞ nên ta đổi nhãn của E thành 13.

    Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là B nên ta khoanh tròn đỉnh B (đỉnh gần M thứ hai).

    – Trong các đỉnh chưa được khoanh tròn, đỉnh kề với B gồm D, F, ta có:

    ⦁ nD = nB + wBD = 4 + 8 = 12.Vì 12 > 11 (11 là nhãn hiện tại của D) nên ta giữ nguyên nhãn của D là 11.

    ⦁ nF = nB + wBF = 4 + 6 = 10.Vì 10 < ∞ nên ta đổi nhãn của F thành 10.

    Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là C nên ta khoanh tròn đỉnh C (đỉnh gần M thứ ba).

    – Trong các đỉnh chưa được khoanh tròn, đỉnh kề với C gồm E, F, ta có:

    ⦁ nE = nC + wCE = 5 + 6 = 11.Vì 11 < 13 (13 là nhãn hiện tại của E) nên ta đổi nhãn của E thành 11.

    ⦁ nF = nC + wCF = 5 + 8 = 13.Vì 13 > 10 (10 là nhãn hiện tại của F) nên ta giữ nguyên nhãn của F là 10.

    Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là F nên ta khoanh tròn đỉnh F (đỉnh gần M thứ tư).

    – Trong các đỉnh chưa được khoanh tròn, đỉnh kề với F chỉ có N, ta có:

    nN = nF + wFN = 10 + 12 = 22.Vì 22 < ∞ nên ta đổi nhãn của N thành 22.

    Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là D, E nên ta tùy ý khoanh tròn đỉnh E (đỉnh gần M thứ năm).

    – Trong các đỉnh chưa được khoanh tròn, đỉnh kề với E chỉ có N, ta có:

    nN = nE + wEN = 11 + 7 = 18.Vì 18 < 22 (22 là nhãn hiện tại của N) nên ta đổi nhãn của N thành 18.

    Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là D nên ta tùy ý khoanh tròn đỉnh D (đỉnh gần M thứ sáu).

    – Trong các đỉnh chưa được khoanh tròn, đỉnh kề với D chỉ còn N, ta có:

    nN = nD + wDN = 11 + 9 = 20.Vì 20 > 18 (18 là nhãn hiện tại của N) nên ta giữ nguyên nhãn của N là 18.

    Lúc này, ta thấy chỉ còn đỉnh N chưa được khoanh tròn nên ta khoanh tròn đỉnh N (đỉnh gần M thứ bảy).

    – Nhìn lại các bước trên, ta thấy:

    nN = 18 = nE + wEN = nC + wCE + wEN = nM + wMC + wCE + wEN

    = wMC + wCE + wEN = lMCEN.

    Vậy MCEN là đường đi ngắn nhất từ đỉnh M đến N, với độ dài bằng 18.

     

    Xem thêm lời giải bài tập Chuyên đề Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác:

    Bài 1 trang 67 Chuyên đề Toán 11: Số đỉnh, số cạnh của đồ thị ở Hình 1 lần lượt là

    Bài 2 trang 67 Chuyên đề Toán 11: Tổng tất cả bậc của các đỉnh của đồ thị ở Hình 1 là

    Bài 3 trang 67 Chuyên đề Toán 11: Đồ thị ở Hình 2 có bao nhiêu đỉnh bậc lẻ?

    Bài 4 trang 67 Chuyên đề Toán 11: Cho đồ thị ở Hình 3, phát biểu nào sau đây đúng?

    Bài 5 trang 67 Chuyên đề Toán 11: Cho đồ thị có trọng số như Hình 4. Đường đi ngắn nhất từ A đến C là

    Bài 6 trang 67 Chuyên đề Toán 11: Cho tập hợp số V = {1; 2; 3; 4; 5; 6; 7}. Hãy vẽ đồ thị G...

    Bài 7 trang 67 Chuyên đề Toán 11: Mỗi đồ thị trong Hình 5 có chu trình Euler không? Nếu có hãy chỉ ra một chu trình...

    Bài 8 trang 68 Chuyên đề Toán 11: Mỗi đồ thị trong Hình 6 có chu trình Hamilton không?...

    Bài 9 trang 68 Chuyên đề Toán 11: Có thể vẽ mỗi hình sau đây bằng một nét liền, không nhấc bút khỏi giấy...

    Bài 10 trang 68 Chuyên đề Toán 11: Tìm đường đi ngắn nhất từ đỉnh M đến N trong đồ thị có trọng số sau:

    Xem thêm lời giải bài tập Chuyên đề Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác:

    Bài 2: Đường đi Euler và đường đi Hamilton

    Bài 3: Bài toán tìm đường đi ngắn nhất

    Bài 1: Hình biểu diễn của một hình, khối

    Bài 2: Bản vẽ kĩ thuật

    Bài tập cuối chuyên đề 3

     

    Tham khảo các loạt bài Toán 11 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 263 03/07/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: