Lấy điểm M trên đường thẳng QR sao cho PM = 4,5cm. Có mấy điểm M như vậy
Với giải Bài 14 trang 60 sgk Toán 7 Tập 2 được biên soạn lời giải chi tiết sẽ giúp học sinh biết cách làm bài tập môn Toán 7. Mời các bạn đón xem:
Giải Toán 7 Luyện tập trang 59, 60
Video giải Bài 14 trang 60 Toán lớp 7 Tập 2
Bài 14 trang 60 Toán lớp 7 Tập 2: Đố: Vẽ tam giác PQR có PQ = PR = 5cm, QR = 6 cm.
Lấy điểm M trên đường thẳng QR sao cho PM = 4,5cm. Có mấy điểm M như vậy?
Điểm M có nằm trên cạnh QR hay không? Tại sao?
Lời giải
* Vẽ hình:
- Vẽ tam giác PQR có PQ = PR = 5cm, QR = 6cm.
+ Vẽ đoạn thẳng QR = 6cm.
+ Vẽ cung tròn tâm Q và cung tròn tâm R bán kính 5cm. Hai cung tròn này cắt nhau tại P.
+ Nối PQ và PR ta được tam giác cần vẽ.
- Vẽ điểm M : Vẽ cung tròn tâm P bán kính 4,5cm cắt QR (nếu có) tại M.

Vậy ta có thể vẽ được 2 điểm M trên đường thẳng QR để PM = 4,5cm
* Kẻ đường cao PH của ΔPQR:
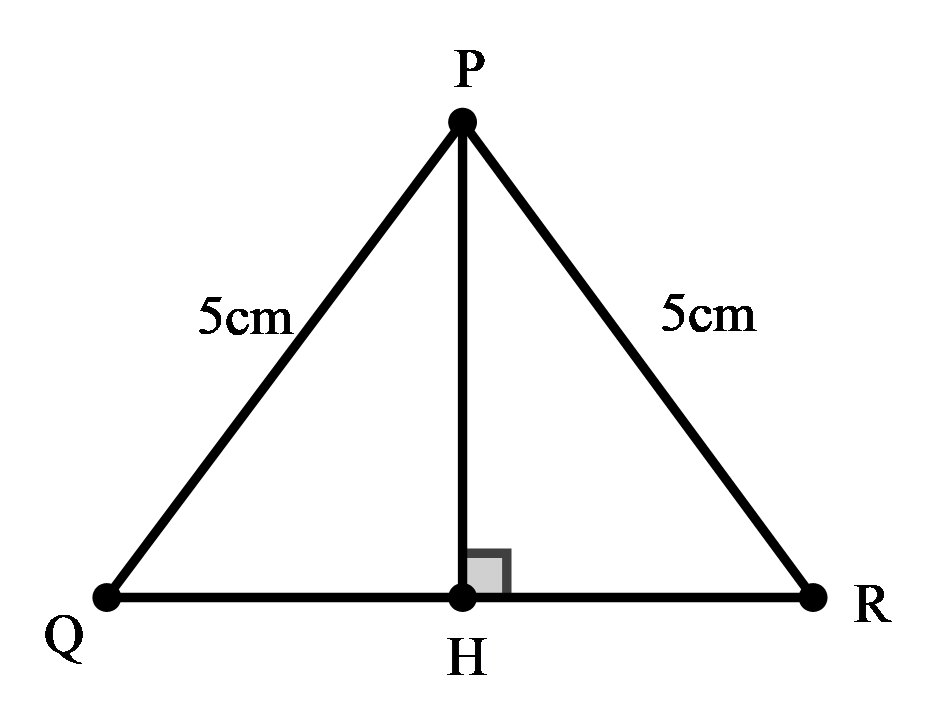
Xét hai tam giác vuông tại H: ΔPHQ và ΔPHR có:
PH là cạnh chung
PQ = PR (= 5cm)
Suy ra ΔPHQ = ΔPHR (cạnh huyền – cạnh góc vuông)
Do đó HQ = HR (hai cạnh tương ứng).
Mà HQ + HR = QR = 6 cm
+ ΔPHR vuông tại H có PR2 = PH2 + HR2 (định lí Py – ta – go)
⇒ PH2 = PR2 - HR2 = 52 – 32 = 16
⇒ PH = 4 (cm).
Đường vuông góc PH = 4cm là đường ngắn nhất trong các đường kẻ P đến đường thẳng QR.
Vậy chắc chắn có đường xiên PM = 4,5cm (vì 4,5cm > 4cm) kẻ từ P đến đường thẳng QR.
+ Lại có HM, HR lần lượt là hình chiếu của các đường xiên PM, PR trên đường thẳng QR.
Mà PM < PR ⇒ HM < HR ; HM < HQ (quan hệ giữa đường xiên và hình chiếu)
⇒ M nằm giữa H và Q hoặc H và R.
⇒ M nằm trên cạnh QP và có hai điểm M như vậy.
Xem thêm lời giải bài tập Toán lớp 7 hay, chi tiết khác:
Bài 11 trang 60 Toán 7 Tập 2: Một cách chứng minh khác của định lí 2...
Bài 13 trang 60 Toán 7 Tập 2: Cho hình 16. Hãy chứng minh rằng: a) BE < BC...
Xem thêm các chương trình khác:
