Trắc nghiệm Vật lí 10 Bài 5. Tốc độ và vận tốc có đáp án
Trắc nghiệm Vật lí 10 Bài 5. Tốc độ và vận tốc có đáp án
-
1102 lượt thi
-
10 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
17/07/2024Người ta thường dùng quãng đường đi được trong cùng một đơn vị thời gian để xác định độ nhanh, chậm của chuyển động. Đại lượng này gọi là
 Xem đáp án
Xem đáp án
Đáp án đúng là: A.
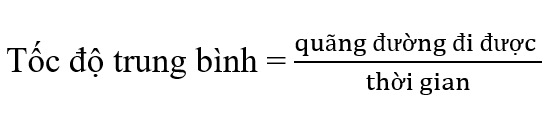
Câu 2:
23/07/2024Công thức nào sau đây là công thức tính tốc độ trung bình?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D.
A - đúng.
B - đúng.
C – sai vì đây là công thức vận tốc trung bình
Câu 3:
18/11/2024Tốc độ tức thời cho biết
 Xem đáp án
Xem đáp án
Đáp án đúng là: D.
- Tốc độ tức thời cho biết Mức độ nhanh chậm của chuyển động tại một thời điểm xác định và tốc độ tại một thời điểm xác định.
- C sai vì đây là vận tốc tức thời.
→ D đúng.A,B,C sai.
* Tốc độ
1. Tốc độ trung bình
- Ta tính được tốc độ trung bình của một vật chuyển động nếu biết quãng đường mà nó di chuyển và thời gian để đi hết quãng đường ấy:
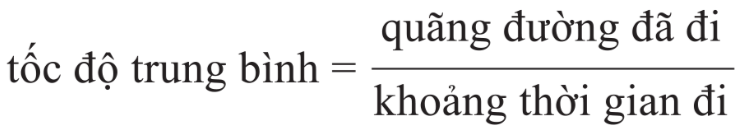
- Nếu kí hiệu: vtb là tốc độ trung bình, s là quãng đường vật đi được trong thời gian t thì:
vtb=st
- Tốc độ trung bình tính trong một thời gian rất ngắn được gọi là tốc độ tức thời.
2. Đơn vị đo tốc độ
- Quãng đường được đo bằng mét (m)
- Thời gian được đo bằng giây (s)
![]() Do đó: tốc độ được tính bằng mét trên giây (m/s)
Do đó: tốc độ được tính bằng mét trên giây (m/s)
- Lưu ý: Việc lựa chọn đơn vị đo còn phụ thuộc vào tình huống.
Xem thêm các bài viết liên quan,chi tiết khác:
Lý thuyết Vật lí 10 Bài 1: Tốc độ, độ dịch chuyển và vận tốc
Giải bài tập Vật lí lớp 10 Bài 1: Tốc độ, độ dịch chuyển và vận tốc
Câu 4:
17/07/2024Vận tốc trung bình là đại lượng được đo bởi:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B.
A – sai vì đây là công thức tốc độ trung bình.
B - đúng vì →v=→dt.
C - sai.
D - sai.
Câu 5:
21/07/2024Hai xe ô tô chạy cùng chiều trên một đoạn đường thẳng với vận tốc 100 km/h và 80 km/h. Tính vận tốc của xe thứ nhất so với xe thứ 2. Chọn chiều dương là chiều chuyển động của hai xe.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A.
Gọi v1,3: là vận tốc của xe thứ nhất so với đường.
v1,2: là vận tốc của xe thứ nhất so với xe thứ hai.
v2,3: là vận tốc của xe thứ hai so với đường.
→v1,3=→v1,2+→v2,3⇒→v1,2=→v1,3−→v2,3
Mà →v1,3↑↑→v2,3 và cùng chiều dương đã chọn, suy ra:
v1,2=v1,3−v2,3=100−80=20(km/h).
Câu 6:
23/07/2024Hai xe ô tô chạy ngược chiều trên một đoạn đường thẳng với vận tốc của xe thứ nhất là 100 km/h và xe thứ hai là 80 km/h. Tính vận tốc của xe thứ nhất so với xe thứ 2. Chọn chiều dương là chiều chuyển động của xe thứ nhất.
 Xem đáp án
Xem đáp án
Đáp án đúng là: B.
Gọi v1,3: là vận tốc của xe thứ nhất so với đường.
v1,2: là vận tốc của xe thứ nhất so với xe thứ hai.
v2,3: là vận tốc của xe thứ hai so với đường.
→v1,3=→v1,2+→v2,3⇒→v1,2=→v1,3−→v2,3
Do hai xe chạy ngược chiều nên →v1,3↑↓→v2,3:
v1,2=100−(−80)=180(km/h).
Câu 7:
16/10/2024Hai bên sông AB cách nhau 70 km, một ca nô khi xuôi dòng AB sớm hơn 48 phút so với ca nô khi ngược dòng AB. Vận tốc của ca nô trong nước yên lặng là 30 km/h. Tính vận tốc của dòng nước .
 Xem đáp án
Xem đáp án
Đáp án đúng: A.
*Phương pháp giải
- đôi đơn vị cho đúng khớp cả bài toán
- gọi các ẩn tương ứng với vận tốc của cano với bờ, cano với mặt nước và dòng nước chảy so với bờ
- Áp dụng công thức cộng vectơ
- Từ đó suy ra khi xuôi dòng ( chiều dương ), và khi ngược dòng ( ngược lại - âm)
- Từ đó đưa ra phương trình thời gian xuôi và thời gian ngược với nhau ( do cano đi xuôi sớm hơn 48 phút ) nên sẽ là thời gian ngược - thời gian xuôi = 48 phút. Thay công thức t=s/v vào để tìm ra v dòng nước so với bờ
*Lời giải:
Đổi 48 phút = 0,8 giờ.
Gọi v1,3: là vận tốc của ca nô so với bờ.
v1,2: là vận tốc của ca nô so với mặt nước.
v2,3: là vận tốc của nước chảy đối với bờ.
Công thức cộng vận tốc: →v1,3=→v1,2+→v2,3
Khi xuôi dòng: v1,3=v1,2+v2,3
Khi ngược dòng: v1,3=v1,2−v2,3
Ta có: tn−tx=0,8⇒ABv1,2−v2,3−ABv1,2+v2,3=0,8
⇔7030−v2,3−7030+v2,3=0,8
⇔v2,3=5(km/h).
*Lý thuyết cần nắm và các dạng bài toán về tốc độ và vận tốc:
Tốc độ trung bình
Tốc độ trung bình thường dùng quãng đường đi được trong cùng một đơn vị thời gian để xác định độ nhanh chậm của chuyển động : kí hiệu là v
v=st
Vận tốc tức thời:
- Trong khoảng thời gian rất ngắn Δt , xe rời được một đoạn đường Δs rất ngắn thì độ lớn của vận tốc tức thời của xe được tính bằng:
v=ΔsΔt
- Công thức tính vận tốc tức thời của vật ở những thời điểm khác nhau: v = v0 + a.t (với gốc thời gian lấy ở thời điểm t0 )
Trong đó:
+ v là vận tốc tại thời điểm t (m/s)
+ v0 là vận tốc ban đầu (m/s)
+ a là gia tốc (ms2)
Chú ý:
+ Chuyển động nhanh dần thì v0.a > 0
+ Chuyển động chậm dần thì v0.a < 0
Phương pháp làm:
– Bước 1: Chọn chiều dương và gốc thời gian, (chọn gốc thời gian là thời điểm ban đầu: t0 = 0).
– Bước 2: Tìm gia tốc a và vận tốc ban đầu v0 ở thời điểm t0.
– Bước 3: Viết công thức : v = v0 + a( t – t0 ) . Nếu t0 = 0 thì: v = v0 + a.t
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Tốc độ và vận tốc - Vật lí 10 Kết nối tri thức
Giải Vật lí 10 Bài 5 (Kết nối tri thức): Tốc độ và vận tốc
Câu 8:
23/07/2024Một ca nô xuôi dòng từ A đến B rồi ngược dòng quay về A. Cho biết vận tốc của ca nô so với nước là 15 km/h, vận tốc của nước so với bờ là 3 km/h. Biết AB = 18 km. Tính thời gian chuyển động của ca nô.
 Xem đáp án
Xem đáp án
Đáp án đúng là: B.
Công thức cộng vận tốc: {\vec v_{1,3}} = {\vec v_{1,2}} + {\vec v_{2,3}}
Khi xuôi dòng: {v_{1,{3_x}}} = {v_{1,2}} + {v_{2,3}}
Khi ngược dòng: {v_{1,{3_n}}} = {v_{1,2}} - {v_{2,3}}
Thay số:
Thời gian xuôi dòng: {{\rm{t}}_x} = \frac{{\rm{s}}}{{{v_{1,{3_x}}}}} = \,\frac{{18}}{{15 + 3}} = 1 ( giờ).
Thời gian ngược dòng: {t_n} = \frac{s}{{{v_{1,{3_n}}}}} = \,\frac{{18}}{{15 - 3}} = 1,5 ( giờ ).
t = {t_x} + \,{t_n} = 2,5 giờ.
Câu 9:
23/07/2024Một dòng sông rộng 100 m và dòng nước chảy với vận tốc 3 m/s so với bờ theo hướng Tây - Đông. Một chiếc thuyền đi sang ngang sông với vận tốc 4 m/s so với dòng nước. Tính độ lớn vận tốc của thuyền so với dòng sông.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A.
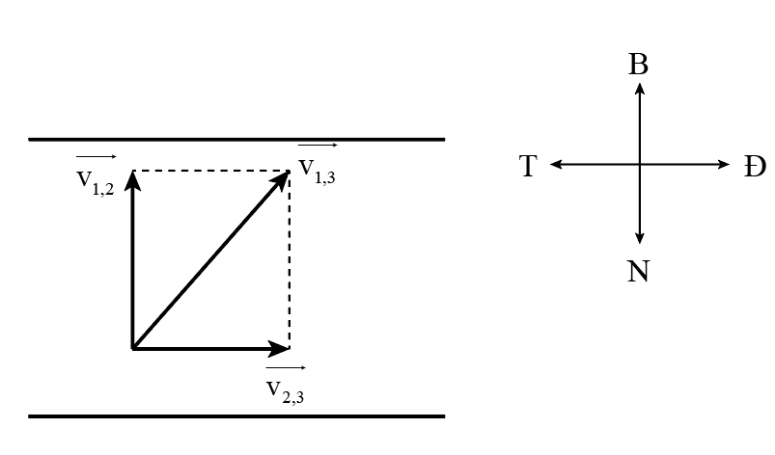
Gọi {v_{1,3}}: là vận tốc của ca nô so với bờ.
{v_{1,2}}: là vận tốc của ca nô so với mặt nước.
{v_{2,3}}: là vận tốc của nước chảy đối với bờ.
Ta có: {\vec v_{1,3}} = {\vec v_{1,2}} + {\vec v_{2,3}}
Mà {\vec v_{1,2}} \bot {\vec v_{2,3}}nên {v_{1,3}} = \sqrt {v_{1,2}^2 + v_{2,3}^2} = \sqrt {{4^2} + {3^2}} = 5(m/s).
Câu 10:
19/07/2024Một dòng sông rộng 100 m và dòng nước chảy với vận tốc 3 m/s so với bờ theo hướng Tây- Đông. Một chiếc thuyền đi sang ngang sông với vận tốc 4 m/s so với dòng nước. Tính quãng đường mà thuyền đã chuyển động được khi sang bên kia sông.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A.
Gọi {v_{1,3}}: là vận tốc của ca nô so với bờ.
{v_{1,2}}: là vận tốc của ca nô so với mặt nước.
{v_{2,3}}: là vận tốc của nước chảy đối với bờ.
Ta có: {\vec v_{1,3}} = {\vec v_{1,2}} + {\vec v_{2,3}}
Mà {\vec v_{1,2}} \bot {\vec v_{2,3}}nên {v_{1,3}} = \sqrt {v_{1,2}^2 + v_{2,3}^2} = \sqrt {{4^2} + {3^2}} = 5(m/s).
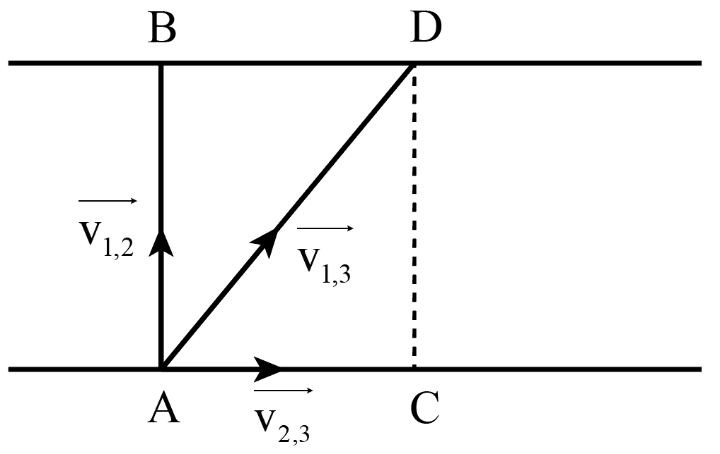
Thời gian thuyền đi từ A đến D với vận tốc {v_{1,3}} bằng thời gian một vật đi từ A đến B với vận tốc {v_{1,2}} nên {\rm{t = }}\frac{{100}}{4} = 25(s).
Suy ra : {\rm{s = AD = 25}}{\rm{.5 = 125 (m)}}{\rm{.}}
Có thể bạn quan tâm
- Trắc nghiệm Vật lí 10 Bài 5. Tốc độ và vận tốc có đáp án (1101 lượt thi)
Các bài thi hot trong chương
- Trắc nghiệm Vật lí 10 Bài 4: Độ dịch chuyển và quãng đường đi được có đáp án (1849 lượt thi)
- Trắc nghiệm Vật lí 10 Bài 7: Đồ thị độ dịch chuyển - thời gian có đáp án (730 lượt thi)
- Trắc nghiệm Vật lí 10 Bài 9. Chuyển động thẳng biến đổi đều có đáp án (719 lượt thi)
- Trắc nghiệm Vật lí 10 Bài 12. Chuyển động ném có đáp án (664 lượt thi)
- Trắc nghiệm Vật lí 10 Bài 10. Sự rơi tự do có đáp án (550 lượt thi)
- Trắc nghiệm Vật lí 10 Bài 8: Chuyển động biến đổi. Gia tốc có đáp án (520 lượt thi)
