Trắc nghiệm Toán 10(có đáp án): Tổng hợp câu hay và khó chương I
Trắc nghiệm Toán 10(có đáp án): Tổng hợp câu hay và khó chương I
-
326 lượt thi
-
12 câu hỏi
-
20 phút
Danh sách câu hỏi
Câu 1:
20/07/2024Lớp 10A có 10 học sinh giỏi Toán, 10 học sinh giỏi Lý, 11 học sinh giỏi Hóa, 6 học sinh giỏi cả Toán và Lý, 5 học sinh giỏi cả Hóa và Lý, 4 học sinh giỏi cả Toán và Hóa, 3 học sinh giỏi cả ba môn Toán, Lý, Hóa. Số học sinh giỏi ít nhất một trong ba môn (Toán, Lý, Hóa) của lớp 10A là:
 Xem đáp án
Xem đáp án
Đáp án A
Theo giả thiết đề bài cho, ta có biểu đồ Ven:
Dựa vào biểu đồ Ven ta thấy:
Số học sinh chỉ giỏi Toán và Lý (không giỏi Hóa) là: 6−3=3 (em)
Số học sinh chỉ giỏi Toán và Hóa (không giỏi Lý) là: 4−3=1 (em)
Số học sinh chỉ giỏi Lý và Hóa (không giỏi Toán) là: 5−3=2 (em)
Số học sinh chỉ giỏi một môn Toán là: 10−3−3−1=3 (em)
Số học sinh chỉ giỏi một môn Lý là: 10−3−3−2=2 (em)
Số học sinh chỉ giỏi một môn Hóa là: 11−1−3−2=5 (em)
Số học sinh giỏi ít nhất một trong ba môn là:
3+2+5+1+2+3+3=19 (em)
Câu 2:
23/07/2024Cho các tập hợp khác rỗng A= [m−1;m+32] và B = (−∞;−3) . Tập hợp các giá trị thực của m để là:
 Xem đáp án
Xem đáp án
Đáp án C
Câu 3:
20/07/2024Cho các tập hợp khác rỗng A = (−; m) và B = [2m−2; 2m+2]. Tìm m R để
 Xem đáp án
Xem đáp án
Đáp án C
Câu 5:
21/11/2024Cho A = . Điều kiện cần và đủ của m sao cho B là tập con của A là:
 Xem đáp án
Xem đáp án
Đáp án đúng: D
*Lời giải
*Phương pháp giải
- Dùng trục số biểu diễn các tập con của tập số thực R
*Lý thuyến cần nắm và dạng toán về mệnh đề và tập hợp:
Các tập con thường dùng của ℝ
- Một số tập con thường dùng của tập số thực ℝ:
+ Khoảng:
(a;b)={x∈R|a<x<b}

(a;+∞)={a∈R|x>a}

(−∞;b)={x∈R|x<b}

(−∞;+∞)

+ Đoạn
[a;b]={x∈R|a≤x≤b}

+ Nửa khoảng
[a;b)={x∈R|a≤x<b}

(a;b]={x∈R|a<x≤b}

[a;+∞)={x∈R|x≥a}

(−∞;b]={x∈R|x≤b}

- Kí hiệu + ∞: Đọc là dương vô cực (hoặc dương vô cùng).
- Kí hiệu – ∞: Đọc là âm vô cực (hoặc âm vô cùng).
- a, b gọi là các đầu mút của đoạn, khoảng hay nửa khoảng.
Giao của hai tập hợp
Tập hợp gồm các phần tử thuộc cả hai tập hợp S và T gọi là giao của hai tập hợp S và T, kí hiệu là S ∩ T.
S ∩ T ={x | x ∈ S và x ∈ T}.
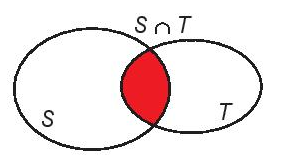
Hợp của hai tập hợp
- Tập hợp gồm các phần tử thuộc tập hợp S hoặc thuộc tập hợp T gọi là hợp của hai tập hợp S và T, kí hiệu là S ∪ T.
S ∪ T = {x | x ∈ S hoặc x ∈ T}.
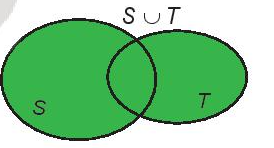
Hiệu của hai tập hợp
- Hiệu của hai tập hợp S và T là tập hợp gồm các phần tử thuộc S nhưng không thuộc T, kí hiệu là S \ T.
S \ T = {x | x ∈ S và x ∉ T}.
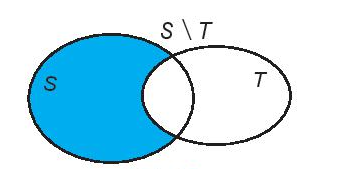
- Nếu T ⊂ S thì S \ T được gọi là phần bù của T trong S, kí hiệu CST.
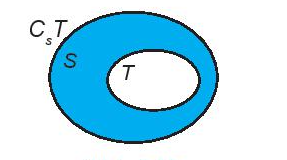
Chú ý: .CsS=∅
Xem thêm các bài viết liên quan hay, chi tiết:
Câu 7:
20/07/2024Cho ba tập hợp:
M: tập hợp các tam giác có 2 góc tù.
N: tập hợp các tam giác có độ dài ba cạnh là ba số nguyên liên tiếp.
P: tập hợp các số nguyên tố chia hết cho 3.
Tập hợp nào là tập hợp rỗng?
 Xem đáp án
Xem đáp án
Đáp án C
Câu 8:
23/07/2024Xác định số phần tử của tập hợp
X={}
 Xem đáp án
Xem đáp án
Đáp án A
Các số tự nhiên chia hết cho 4 nhỏ hơn 2017 là 0;4;8;...;2016
Số phần tử của tập hợp X là: (2016−0):4+1 = 505 (số)
Vậy có tất cả 505 số tự nhiên nhỏ hơn 2017 và chia hết cho 4.
Câu 9:
23/07/2024Cho hai tập hợp A = [1;3] và B = [m; m+1]. Tìm tất cả giá trị của tham số m để BA.
 Xem đáp án
Xem đáp án
Đáp án C
Câu 10:
20/07/2024Cho m là một tham số thực và hai tập hợp khác rỗng A = [1−2m; m+3], B = {8−5m}. Tất cả các giá trị m để là:
 Xem đáp án
Xem đáp án
Đáp án D
Câu 11:
14/10/2024Lớp 10A có 7 học sinh giỏi Toán, 5 học sinh giỏi Lý, 6 học sinh giỏi Hoá, 3 học sinh giỏi cả Toán và Lý, 4 học sinh giỏi cả Toán và Hoá, 2 học sinh giỏi cả Lý và Hoá, 1 học sinh giỏi cả ba môn Toán, Lý, Hoá. Số học sinh giỏi ít nhất một môn (Toán, Lý, Hoá ) của lớp 10A là:
 Xem đáp án
Xem đáp án
Đáp án đúng: C
*Phương pháp giải
- vẽ biểu đồ Ven ra để nhìn cho rõ những số học sinh giỏi cả 2 môn và 3 môn
- Từ đó để tính được số học sinh giỏi chỉ 2 môn. TT để tìm ra số học sinh chỉ giỏi ít nhất 1 trong 3 môn
*Lời giải
Dựa vào biểu đồ Ven ta thấy:
Số học sinh giỏi toán, lý mà không giỏi hóa: 3−1=2.
Số học sinh giỏi toán, hóa mà không giỏi lý: 4−1=3.
Số học sinh giỏi hóa, lý mà không giỏi toán: 2−1=1.
Số học sinh chỉ giỏi môn lý: 5−2−1−1=1.
Số học sinh chỉ giỏi môn hóa: 6−3−1−1=1.
Số học sinh chỉ giỏi môn toán: 7−3−2−1=1.
Số học sinh giỏi ít nhất một (môn toán, lý, hóa) là số học sinh giỏi 1 môn hoặc 2 môn hoặc cả 3 môn: 1+1+1+1+2+3+1=10.
* Phương pháp giải toán sử dụng biểu đồ Ven:
+ Bước 1: Chuyển bài toán về ngôn ngữ tập hợp.
+ Bước 2: Sử dụng sơ đồ Ven để minh họa các tập hợp.
Vẽ các vòng kín đại diện các tập hợp (mỗi vòng kín là một tập hợp), lưu ý hai vòng kín có phần chung nếu mỗi vòng kín có ít nhất một phần nằm trong vòng kín kia và hai tập hợp đó khác rỗng.
+ Bước 3: Dựa vào sơ đồ Ven ta thiết lập được đẳng thức hoặc phương trình, hệ phương trình, từ đó tìm được kết quả bài toán.
Lưu ý:
+ Nếu A và B là hai tập hợp hữu hạn thì n(A ∪ B) = n(A) + n(B) – n(A ∩ B).
⇒ n(A ∩ B) = n(A) + n(B) – n(A ∪ B).
+ Nếu A và B không có phần tử chung, tức là A ∩ B = ∅, thì n(A ∪ B) = n(A) + n(B).
Xem thêm các bài viết liên quan hay chi tiết:
Lý thuyết Tập hợp và các phép toán trên tập hợp - Toán 10 Kết nối tri thức
Giải SBT Toán 10 Bài 2. Tập hợp và các phép toán trên tập hợp có đáp án
Các phép toán trên tập hợp và cách giải bài tập hay nhất
