Dạng 9: Ứng dụng của hàm số bậc hai để giải bài toán thực tế có đáp án
-
1697 lượt thi
-
12 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
21/07/2024
Xem đáp án
Hướng dẫn giải:
Chọn hệ trục tọa độ Oxy.
Với g = 9,8 m/s2, góc phát cầu α = 30°, vận tốc ban đầu v0 = 8 m/s, phương trình quỹ đạo của cầu là:
\(y = - \frac{{9,8{x^2}}}{{{{2.8}^2}.co{s^2}({{30}^o})}} + \tan ({30^o}).x + 0,7 = \frac{{ - 4,9}}{{48}}{x^2} + \frac{{\sqrt 3 }}{3}x + 0,7\)
Vị trí cầu rơi chạm đất là giao điểm của parabol và trục hoành nên giải phương trình
\(\frac{{ - 4,9}}{{48}}{x^2} + \frac{{\sqrt 3 }}{3}x + 0,7 = 0\) ta được x1 ≈ –1,03 và x2 ≈ 6,68
Giá trị nghiệm dương cho ta khoảng cách từ vị trí người chơi cầu lông đến vị trí cầu rơi chạm đất khoảng 6,68 m.
Câu 2:
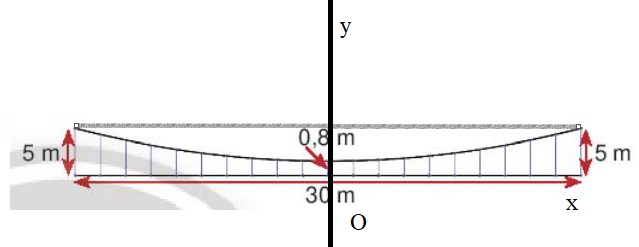
20/07/2024Chiếc cầu dây văng một nhịp được thiết kế hai bên thành cầu có dạng parabol và được cố định bằng các dây cáp song song.
Dựa vào bản vẽ ở Hình 14, hãy tính chiều dài tổng cộng của các dây cáp dọc ở hai mặt bên. Biết:
– Dây dài nhất là 5m, dây ngắn nhất là 0,8 m. Khoảng cách giữa các dây bằng nhau.
– Nhịp cầu dài 30 m.
– Cần tính thêm 5% chiều dài mỗi sợi dây cáp để neo cố định.
Xem đáp án
Hướng dẫn giải:
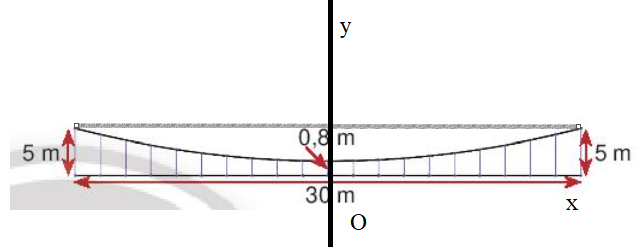
Chọn hệ trục tọa độ như hình vẽ.
Trong đó, khoảng cách giữa các dây bằng nhau và có 20 khoảng cách nên mỗi khoảng cách ứng với 1,5 m.
Gọi dạng parabol của thành cầu là đồ thị của hàm số y = ax2 + bx + c (a ≠ 0).
Đồ thị hàm số cắt trục tung tại điểm (0; 0,8) nên ta có:
a.02 + b.0 + c = 0,8 ⇒ c = 0,8
Tại hai đầu cầu, tức y = 5 thì ta có hai giá trị x thỏa mãn là x1 = –15 và x2 = 15
Từ đó ta có:
a.(–15)2 + b.(–15) + 0,8 = 5 ⇒ 225a – 15b = 4,2 (1)
a.152 + b.15 + 0,8 = 5 ⇒ 225a + 15b = 4,2 (2)
Từ (1) và (2) ta có hệ phương trình \(\left\{ \begin{array}{l}225a - 15b = 4,2\\225a + 15b = 4,2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \frac{7}{{375}}\\b = 0\end{array} \right.\)
Vậy phương trình parabol cần tìm là: \(y = \frac{7}{{375}}{x^2} + 0,8\)
Độ dài mỗi dây ở vị trí hoành độ tương ứng là:
Tại x = 0, độ dài dây là: 0,8 + 5%.0,8 = 0,84 (m)
Tại x = 1,5 và x = –1,5 thì độ dài dây là:
\(\frac{7}{{375}}{.1,5^2} + 0,8 + 5\% .\left( {\frac{7}{{375}}{{.1,5}^2} + 0,8} \right) = 0,8841\) (m)
Tại x = 3 và x = –3 thì độ dài dây là:
\(\frac{7}{{375}}{.3^2} + 0,8 + 5\% .\left( {\frac{7}{{375}}{{.3}^2} + 0,8} \right) = 1,0164\) (m)
Tại x = 4,5 và x = –4,5 thì độ dài dây là:
\(\frac{7}{{375}}{.4,5^2} + 0,8 + 5\% .\left( {\frac{7}{{375}}{{.4,5}^2} + 0,8} \right) = 1,2369\) (m)
Tại x = 6 và x = –6 thì độ dài dây là:
\(\frac{7}{{375}}{.6^2} + 0,8 + 5\% .\left( {\frac{7}{{375}}{{.6}^2} + 0,8} \right) = 1,5456\) (m)
Tại x = 7,5 và x = –7,5 thì độ dài dây là:
\(\frac{7}{{375}}{.7,5^2} + 0,8 + 5\% .\left( {\frac{7}{{375}}{{.7,5}^2} + 0,8} \right) = 1,9425\) (m)
Tại x = 9 và x = –9 thì độ dài dây là:
\(\frac{7}{{375}}{.9^2} + 0,8 + 5\% .\left( {\frac{7}{{375}}{{.9}^2} + 0,8} \right) = 2,4276\) (m)
Tại x = 10,5 và x = –10,5 thì độ dài dây là:
\(\frac{7}{{375}}{.10,5^2} + 0,8 + 5\% .\left( {\frac{7}{{375}}{{.10,5}^2} + 0,8} \right) = 3,0009\)(m)
Tại x = 12 và x = –12 thì độ dài dây là:
\(\frac{7}{{375}}{.12^2} + 0,8 + 5\% .\left( {\frac{7}{{375}}{{.12}^2} + 0,8} \right) = 3,6624\)(m)
Tại x = 13,5 và x = –13,5 thì độ dài dây là:
\(\frac{7}{{375}}{.13,5^2} + 0,8 + 5\% .\left( {\frac{7}{{375}}{{.13,5}^2} + 0,8} \right) = 4,4121\)(m)
Tại x = 15 và x = –15 thì độ dài dây là:
5 + 5%.5 = 5,25 (m)
Chiều dài tổng cộng của các dây cáp dọc ở hai mặt bên của cầu là:
2.0,84 + 4 . (0,8841 + 1,0164 + 1,2369 + 1,5456 + 1,9425 + 2,4276 + 3,0009 + 3,6624 + 4,4121 + 5,25) = 103,194 (m).
Câu 3:
20/07/2024 Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A.
Gọi y là số tiền lãi của cửa hàng bán giày
Ta có: y = (120 – x)(x – 40) = –x2 + 160x – 4800
Xét hàm số y = –x2 + 160x – 4800 có a = –1 < 0 nên hàm số đạt giá trị lớn nhất tại
\(x = \frac{{ - b}}{{2a}} = \frac{{ - 160}}{{2.( - 1)}} = 80\)
Vậy cửa hàng bán một đôi giày giá 80 đô thì thu được nhiều lãi nhất.
Câu 4:
23/07/2024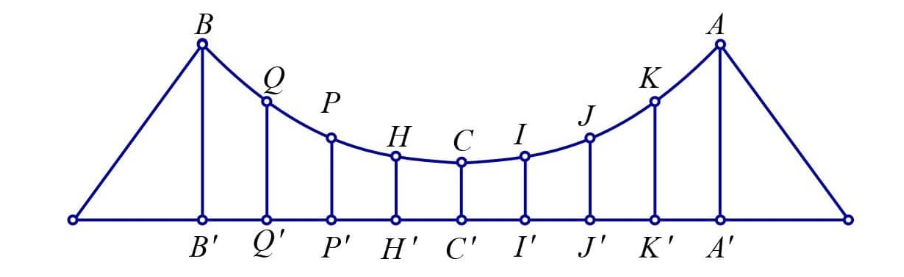
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A.
Giả sử parabol có phương trình: y = ax2 + bx + c (a ≠ 0)
Chọn hệ trục Oxy như hình vẽ, khi đó parabol đi qua điểm A(100; 30) và có đỉnh C(0; 5). Đoạn AB chia làm 8 phần, mỗi phần 25 m.
Suy ra: \(\left\{ \begin{array}{l}30 = 10000a + 100b + c\\\frac{{ - b}}{{2a}} = 0\\5 = c\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \frac{1}{{400}}\\b = 0\\c = 5\end{array} \right. \Leftrightarrow y = \frac{1}{{400}}{x^2} + 5\)
Khi đó, tổng độ dài của các dây cáp treo bằng
OC + 2y1 + 2y2 + 2y3
= \(5 + 2\left( {\frac{1}{{400}}{{.25}^2} + 5} \right) + 2\left( {\frac{1}{{400}}{{.50}^2} + 5} \right) + 2\left( {\frac{1}{{400}}{{.75}^2} + 5} \right) = 78,75\)(m).
Câu 5:
20/07/2024 Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D.
Cầu rời mặt vợt ở độ cao 0,7 m so với mặt đất và vận tốc ban đầu của cầu là 12 m/s (bỏ qua sức cản của gió và xem quỹ đạo của cầu luôn nằm trong mặt phẳng thẳng đứng).
Chọn hệ trục tọa độ Oxy
Với g = 9,8 m/s2, góc phát cầu α = 30°, vận tốc ban đầu v0 = 12 m/s, phương trình quỹ đạo của cầu là:
\(y = \frac{{ - 9,8.{x^2}}}{{{{2.12}^2}.co{s^2}{{30}^o}}} + \tan {30^o}.x + 0,7 = - \frac{{49}}{{1080}}{x^2} + \frac{{\sqrt 3 }}{3}x + 0,7\)(với x ≥ 0)\(\)
Khi x = 4, ta có \(y = - \frac{{49}}{{1080}}{.4^2} + \frac{{\sqrt 3 }}{3}.4 + 0,7 \approx 2,283\)> 1,524
Như vậy, cầu đã vượt qua lưới. Điểm rơi của cầu là giao điểm của parabol và trục hoành nên giải phương trình:
\( - \frac{{49}}{{1080}}{x^2} + \frac{{\sqrt 3 }}{3}x + 0,7 = 0\) ta được: x1 ≈ 13,84 và x2 ≈ –1,11
Giá trị nghiệm dương cho ta khoảng cách từ vị trí người chơi cầu lông đến vị trí cầu rơi chạm đất là 13,84 m.
Câu 6:
18/07/2024 Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B.
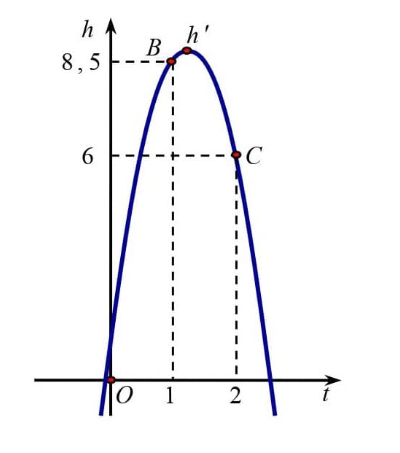
Chọn hệ trục Oth như hình
Tại t = 0 ta có: h = 1,2
Tại t = 1 ta có: h = 8,5
Tại t = 2 ta có: h = 6
Parabol có phương trình y = at2 + bt + c (a ≠ 0)
Theo bài ta có: A(0; 1,2), B(1; 8,5), C(2; 6) thuộc parabol
Do đó, có hệ phương trình: \(\left\{ \begin{array}{l}c = 1,2\\a + b + c = 8,5\\4a + 2b + c = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}c = 1,2\\a = - 4,9\\b = 12,2\end{array} \right.\)
Vậy hàm số cần tìm có dạng y = –4,9t2 + 12,2t + 1,2.
Câu 7:
23/07/2024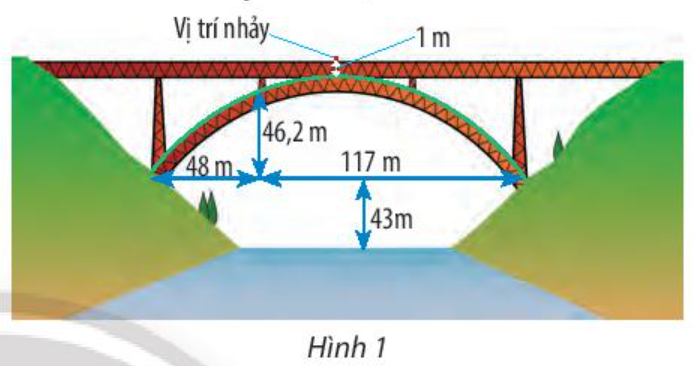
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A.
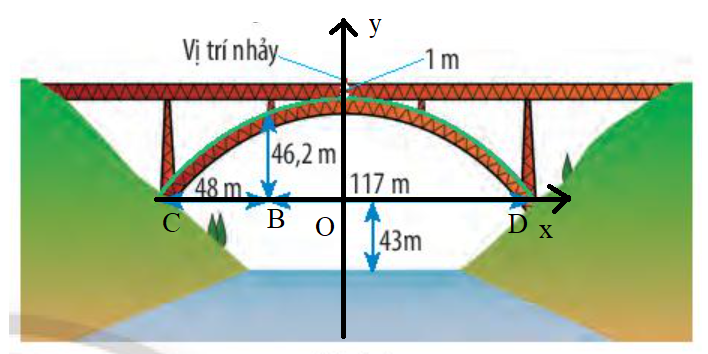
Đặt hệ trục tọa độ Oxy như hình vẽ, gọi phương trình của parabol có dạng: y = ax2 + bx + c (a ≠ 0).
Ta có: OB = CD : 2 – CB = (48 + 117) : 2 – 48 = 34,5 (m)
OC = CD : 2 = (48 + 117) : 2 = 82,5 (m)
Từ đó ta có điểm thuộc parabol là (34,5; 46,2)
⇒ a.34,52 + b.34,5 + c = 46,2
⇒ 1190,26a + 34,5b + c = 46,2 (1)
Ngoài ra, parabol còn cắt trục hoành tại hai điểm (–82,5; 0) và (82,5; 0) nên ta có:
a.(–82,5)2 + b.(–82,5) + c = 0 \( \Rightarrow \)6806,25a – 82,5b + c = 0 (2)
a.82,52 + b.82,5 + c = 0 \( \Rightarrow \) 6806,25a + 82,5b + c = 0 (3)
Từ (1), (2), (3) ta có hệ phương trình: \(\left\{ \begin{array}{l}1190,26a + 34,5b + c = 46,2\\6806,25a - 82,5b + c = 0\\6806,25a + 82,5b + c = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a \approx - 0,008\\b = 0\\c \approx 56\end{array} \right.\)
Xét đỉnh parabol có hoành độ x = 0 và tung độ y = –0,008.02 + 56 = 56.
Khoảng cách từ vị trí nhảy đến mặt nước là: 1 + 56 + 43 = 100 (m)
Vậy độ dài dây an toàn cần thiết là: \(\frac{{100}}{3}\) ≈ 33 m.
Câu 8:
21/07/2024
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B.
Gọi A và B là hai điểm ứng với hai chân cổng như hình vẽ.
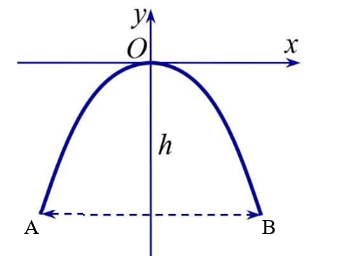
Vì cổng hình parabol có phương trình \(y = - \frac{1}{2}{x^2}\) và cổng có chiều rộng d = 5 m nên:
AB = 5 và hoành độ của A và B lần lượt là \( - \frac{5}{2},\,\,\frac{5}{2}\).
Ta có: \(y = - \frac{1}{2}.{\left( {\frac{5}{2}} \right)^2} = - \frac{1}{2}.{\left( { - \frac{5}{2}} \right)^2} = \frac{{ - 25}}{8}\)
Do đó, \(A\left( {\frac{{ - 5}}{2};\frac{{ - 25}}{8}} \right)\) và \(B\left( {\frac{5}{2};\frac{{ - 25}}{8}} \right)\).
Chiều cao của cổng chính là giá trị tuyệt đối tung độ của A và B hay h = \(\left| {\frac{{ - 25}}{8}} \right| = \frac{{25}}{8} = 3,125\) (m).
Câu 9:
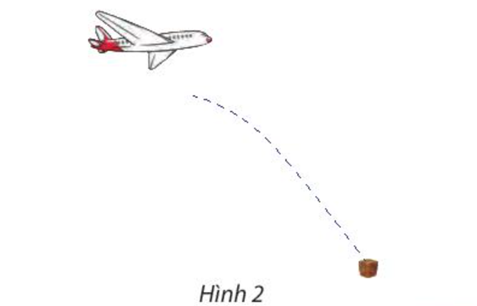
20/07/2024Giả sử một máy bay cứu trợ đang bay theo phương ngang và bắt đầu thả hàng từ độ cao 80 m, lúc đó máy bay đang bay với vận tốc 50 m/s. Để thùng hàng cứu trợ rơi đúng vị trí được chọn, máy bay cần bắt đầu thả hàng từ vị trí cách vị trí được chọn bao nhiêu mét ? Biết rằng nếu chọn gốc tọa độ là hình chiếu trên mặt đất của vị trí hàng cứu trợ bắt đầu được thả, thì tọa độ của hàng cứu trợ được cho bởi hệ sau: \(\left\{ \begin{array}{l}x = {v_o}t\\y = h - \frac{1}{2}g{t^2}\end{array} \right.\)
trong đó, v0 là vận tốc ban đầu và h là độ cao tính từ khi hàng rời máy bay.
Lưu ý: Chuyển động này được xem là chuyển động ném ngang.
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C.
Theo đề bài, ta có biểu thức tọa độ của thùng hàng: \(\left\{ \begin{array}{l}x = 50t\\y = 80 - \frac{1}{2}g{t^2}\end{array} \right.\).
Đặt hệ trục tọa độ như hình vẽ. Khi thùng hàng rơi đúng vị trí, ta có:
y = 0 \( \Leftrightarrow 80 - \frac{1}{2}g{t^2} = 0 \Leftrightarrow \frac{1}{2}g{t^2} = 80 \Leftrightarrow g{t^2} = 160 \Leftrightarrow {t^2} = \frac{{160}}{g} \Leftrightarrow t = \frac{{\sqrt {160} }}{g}\)
Khi đó, ta có: \(x = 50.\frac{{\sqrt {160} }}{g} = \frac{{200\sqrt {10} }}{{9,8}}\) (m)
Vậy để thùng hàng cứu trợ rơi đúng vị trí được chọn, máy bay cần bắt đầu thả hàng từ vị trí cách vị trí được chọn \(\frac{{200\sqrt {10} }}{{9,8}}\) m.
Câu 10:
23/07/2024 Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C.
Gọi x triệu đồng là số tiền mà doanh nghiệp A dự điện giảm giá (0 ≤ x ≤ 4).
Khi đó, lợi nhuận thu được khi bán một chiếc xe là: 31 – x – 27 = 4 – x.
Số xe mà doanh nghiệp sẽ bán được trong một năm là 600 + 200x.
Lợi nhuận mà doanh nghiệp thu được trong một năm là:
y = (4 – x)(600 + 200x) = –200x2 + 200x + 2400
Xét hàm số y = –200x2 + 200x + 2400 ta có a = –200 < 0 do đó, hàm số đạt giá trị lớn nhất tại \(x = \frac{{ - b}}{{2a}} = \frac{{ - 200}}{{2.( - 200)}} = 0,5\) (thỏa mãn điều kiện)
Vậy giá mới của chiếc xe là 31 – 0,5 = 30,5 triệu đồng thì lợi nhuận thu được là cao nhất.
Câu 11:
23/07/2024 Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B.
Trọng lượng cá trên đơn vị diện tích là:
T = (360 – 10n).n = –10n2 + 360n (n > 0)
Xét hàm số bậc hai y = –10n2 + 360n biến n có:
\( - \frac{b}{{2a}} = \frac{{ - 360}}{{2.( - 10)}} = 18\) \[\]
\(\frac{{ - \Delta }}{{4a}} = \frac{{ - ({b^2} - 4ac)}}{{4a}} = \frac{{ - ({{360}^2} - 4.( - 10).0)}}{{4.( - 10)}} = 3240\)
Hàm số có a = –10 < 0 nên hàm số đạt giá trị lớn nhất là 3240 khi n = 18.
Hay phải thả 18 con cá trên một đơn vị diện tích để trọng lượng cá sau một vụ thu được nhiều nhất.
Câu 12:
22/07/2024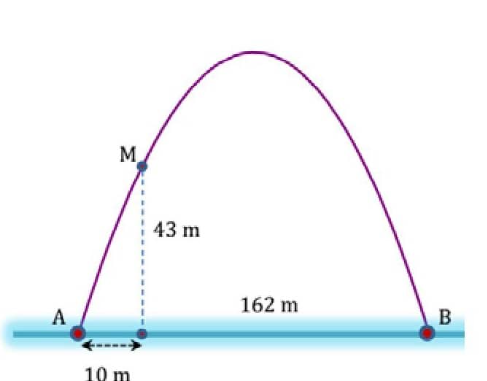
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A.
Chọn hệ trục tọa độ Oxy như hình, A ≡ O.
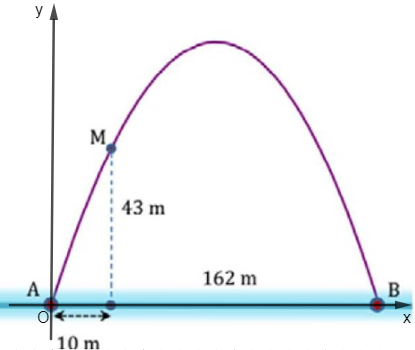
Parabol (P) có phương trình dạng: y = ax2 + bx + c (a ≠ 0).
Parabol đi qua điểm A(0; 0), B(162; 0), M(10; 43) nên ta có:
\(\left\{ \begin{array}{l}c = 0\\{162^2}a + 162b + c = 0\\{10^2}a + 10b + c = 43\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}c = 0\\a = \frac{{ - 43}}{{1520}}\\b = \frac{{3483}}{{760}}\end{array} \right.\)
Do đó, phương trình của (P) là: \(y = - \frac{{43}}{{1520}}{x^2} + \frac{{3483}}{{760}}x\)
Do đó, chiều cao của cổng là tung độ của đỉnh parabol và là:
\(h = - \frac{\Delta }{{4a}} = - \frac{{{b^2} - 4ac}}{{4a}} = - \frac{{{{\left( {\frac{{3483}}{{760}}} \right)}^2} - 4.\left( {\frac{{ - 43}}{{1520}}} \right).0}}{{4.\left( {\frac{{ - 43}}{{1520}}} \right)}} \approx 185,6\) (m).