Trắc nghiệm Toán 10 CTST Bài 2. Giải phương trình bậc hai một ẩn (Phần 2) có đáp án
Trắc nghiệm Toán 10 CTST Bài 2. Giải phương trình bậc hai một ẩn (Thông hiểu) có đáp án
-
463 lượt thi
-
8 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
13/07/2024Cho f(x) = –x2 – 4x + 5. Có bao nhiêu giá trị nguyên của x thỏa mãn f(x) ≥ 0?
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Tam thức bậc hai f(x) = –x2 – 4x + 5 có ∆’ = (–2)2 – (–1).5 = 9 > 0.
Suy ra f(x) có hai nghiệm phân biệt là:
Ta lại có a = –1 < 0.
Do đó ta có:
⦁ f(x) âm trên hai khoảng (–∞; –5) và (1; +∞);
⦁ f(x) dương trên khoảng (–5; 1);
⦁ f(x) = 0 khi x = –5 hoặc x = 1.
Vì vậy bất phương trình f(x) ≥ 0 có tập nghiệm là [–5; 1].
Trên đoạn [–5; 1], ta thấy có 7 giá trị nguyên là: –5; –4; –3; –2; –1; 0; 1.
Vậy ta chọn phương án B.
Câu 2:
22/07/2024Tập nghiệm của bất phương trình x2 – 3x + 2 < 0 là:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Tam thức bậc hai f(x) = x2 – 3x + 2 có ∆ = (–3)2 – 4.1.2 = 1 > 0.
Do đó f(x) có hai nghiệm phân biệt là:
Ta lại có a = 1 > 0.
Do đó ta có:
⦁ f(x) âm trên khoảng (1; 2);
⦁ f(x) dương trên hai khoảng (–∞; 1) và (2; +∞);
⦁ f(x) = 0 khi x = 1 hoặc x = 2.
Vì vậy bất phương trình x2 – 3x + 2 < 0 có tập nghiệm là (1; 2).
Ta chọn phương án A.
Câu 3:
23/07/2024Tập nghiệm của bất phương trình x2 + 9 > 6x là:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Ta có x2 + 9 > 6x.
⇔ x2 – 6x + 9 > 0.
Tam thức bậc hai f(x) = x2 – 6x + 9 có ∆’ = (–3)2 – 1.9 = 0.
Suy ra f(x) có nghiệm kép x = 3.
Ta lại có a = 1 > 0.
Do đó ta có:
⦁ f(x) dương trên hai khoảng (–∞; 3) và (3; +∞);
⦁ f(x) = 0 khi x = 3.
Vì vậy bất phương trình x2 – 6x + 9 > 0 có tập nghiệm là (–∞; 3) ∪ (3; +∞) (hoặc ta có thể viết: ℝ \ {3}).
Ta chọn phương án B.
Câu 4:
20/07/2024Tập xác định của hàm số là:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Hàm số xác định khi và chỉ khi –x2 + 2x + 3 ≥ 0.
Tam thức bậc hai f(x) = –x2 + 2x + 3 có ∆’ = 12 – (–1).3 = 4 > 0.
Do đó f(x) có hai nghiệm phân biệt là:
Ta lại có a = –1 < 0.
Do đó ta có:
⦁ f(x) dương trên khoảng (–1; 3);
⦁ f(x) âm trên hai khoảng (–∞; –1) và (3; +∞);
⦁ f(x) = 0 khi x = –1 hoặc x = 3.
Vì vậy bất phương trình –x2 + 2x + 3 ≥ 0 có tập nghiệm là [–1; 3].
Khi đó hàm số đã cho có tập xác định là [–1; 3].
Ta chọn phương án C.
Câu 5:
14/07/2024Tập xác định của hàm số là:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Hàm số xác định khi và chỉ khi –2x2 + 8x – 12 > 0.
Tam thức bậc hai f(x) = –2x2 + 8x – 12 có ∆’ = 42 – (–2).(–12) = –8 < 0.
Do đó f(x) vô nghiệm.
Ta lại có a = –2 < 0.
Vì vậy f(x) < 0, với mọi x ∈ ℝ.
Vậy bất phương trình –2x2 + 8x – 12 > 0 có tập nghiệm là ∅.
Ta chọn phương án C.
Câu 6:
19/07/2024Cho bất phương trình (m – 2)x2 + 2(2m – 3)x + 5m – 6 ≥ 0. Để x = 6 là một nghiệm của bất phương trình trên thì m nhận giá trị nào trong các giá trị sau đây?
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Vì x = 6 là một nghiệm của bất phương trình (m – 2)x2 + 2(2m – 3)x + 5m – 6 ≥ 0 nên ta có:
(m – 2).62 + 2(2m – 3).6 + 5m – 6 ≥ 0.
⇔ 36(m – 2) + 12(2m – 3) + 5m – 6 ≥ 0
⇔ 65m – 114 ≥ 0
Vậy thỏa mãn yêu cầu bài toán.
Ta chọn phương án A.
Câu 7:
13/07/2024Cho hàm số bậc hai f(x) có đồ thị như hình bên.
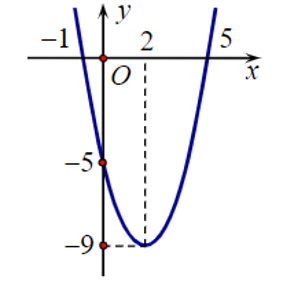
Tập nghiệm của bất phương trình f(x) ≥ 0 là:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Quan sát đồ thị, ta thấy f(x) ≥ 0 khi và chỉ khi x ≤ –1 hoặc x ≥ 5.
Vì vậy tập nghiệm của bất phương trình f(x) ≥ 0 là (–∞; –1] ∪ [5; +∞).
Ta chọn phương án C.
Câu 8:
23/07/2024Tập nghiệm của bất phương trình (2x – 5)(x + 2) ≥ x2 – 4 là:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Ta có (2x – 5)(x + 2) ≥ x2 – 4.
⇔ 2x2 – x – 10 ≥ x2 – 4.
⇔ x2 – x – 6 ≥ 0.
Tam thức bậc hai f(x) = x2 – x – 6 có ∆ = (–1)2 – 4.1.(–6) = 25 > 0.
Suy ra f(x) có hai nghiệm phân biệt là:
Ta lại có a = 1 > 0.
Vì vậy:
⦁ f(x) dương với mọi x thuộc hai khoảng (–∞; –2) và (3; +∞);
⦁ f(x) âm với mọi x thuộc khoảng (–2; 3);
⦁ f(x) = 0 khi x = –2 hoặc x = 3.
Vậy bất phương trình x2 – x – 6 ≥ 0 có tập nghiệm là (–∞; –2] ∪ [3; +∞).
Do đó ta chọn phương án D.