Trắc nghiệm Toán 10 CTST Bài 1: Xác định vectơ. Tìm điểm đầu, điểm cuối, giá của vectơ có đáp án
Dạng 4: Chứng minh hai vectơ bằng nhau, hai vectơ đối nhau có đáp án
-
924 lượt thi
-
10 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
15/07/2024Cho tam giác ABC có M, N lần lượt là trung điểm của AB và AC như hình vẽ.
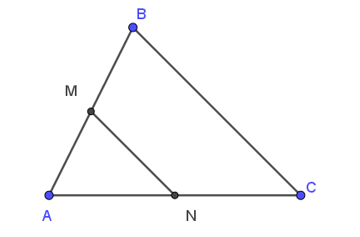
Vectơ nào bằng vectơ →NA ?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A.
Xét tam giác ABC có: N là trung điểm của AC, do đó: NA = CN ⇒|→NA|=|→CN|
Ta có: →NA và →CN có cùng giá là đường thẳng AC.
Nên hai vectơ →NA và →CN cùng phương.
Mà →NA và →CN cùng hướng từ phải sang trái.
Vậy →NA = →CN.
Câu 2:
19/07/2024Cho tam giác ABC có M, N lần lượt là trung điểm của AB và AC. Vectơ nào là vectơ đối của vectơ →BM ?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C.
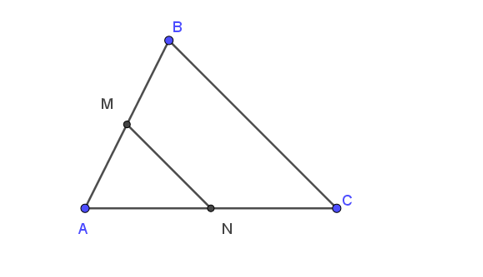
Xét tam giác ABC có: M là trung điểm của AB, do đó: AM = BM ⇒|→BM|=|→AM|
Ta có: hai vectơ →BM và →AM có cùng giá là đường thẳng AB.
Mà →BM có hướng từ phải sang trái và →AM có hướng từ trái sang phải
Do đó, chúng ngược hướng.
Vậy hai vectơ →BM và →AM đối nhau.
Câu 3:
15/07/2024Cho tam giác ABC có M, N, P lần lượt là trung điểm các cạnh AB, AC, BC của tam giác ABC. Vectơ nào sau đây bằng vectơ →NC.
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B.
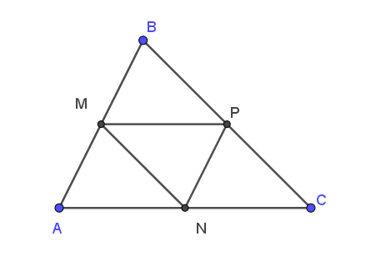
Xét tam giác ABC có:
N là trung điểm của AC có: NC = 12AC (1)
M là trung điểm của AB, P là trung điểm của BC nên MP là đường trung bình của tam giác ABC, do đó: MP = 12AC (2), MP // AC (3)
Từ (1) và (2) ta suy ra: NC = MP hay |→NC|=|→MP|.
Từ (3) ta có: hai vectơ →NC và →MP cùng phương, mà chúng cùng hướng đi từ trái sang phải.
Vậy →NC = →MP.
Câu 4:
16/07/2024Cho tam giác ABC có M, N, P lần lượt là trung điểm các cạnh AB, AC, BC của tam giác ABC. Vectơ nào sau đây là vectơ đối của →PN.
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D.
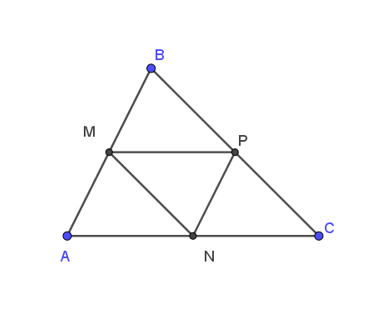
Xét tam giác ABC có:
M là trung điểm của AB có: MB = 12AB (1)
P là trung điểm của BC, N là trung điểm của AC nên PN là đường trung bình của tam giác ABC, do đó: PN = 12AB (2), PN // AB (3)
Từ (1) và (2) ta suy ra: MB = PN hay |→MB|=|→PN|
Từ (3) ta có: hai vectơ →PN và →MB cùng phương, mà chúng ngược hướng nhau.
Vậy hai vectơ →PN và →MB đối nhau.
Câu 5:
22/07/2024Cho hình vuông ABCD tâm O như hình vẽ sau:
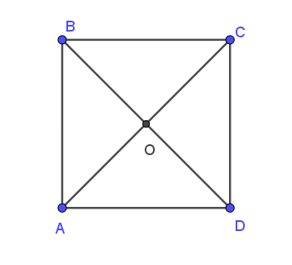
Vectơ nào sau đây bằng vectơ →OA?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A.
Xét hình vuông ABCD tâm O có:
OA = CO = 12AC
⇒|→OA|=|→CO| (1)
Mặt khác, →OA và →CO có cùng giá là đường thẳng AC
Do đó, →OA và →CO cùng phương, mà chúng cùng hướng (2)
Từ (1) và (2) ta kết luận: →CO = →OA.
Câu 6:
20/07/2024Cho hình vuông ABCD tâm O.
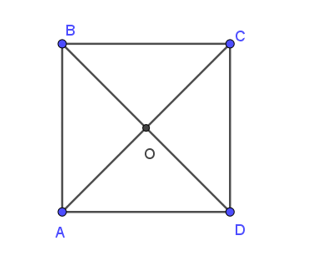
Khẳng định nào sau đây là đúng ?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D.
Xét hình vuông ABCD tâm O có:
OB = OD = 12BD
⇒|→OB|=|→OD| (1)
Mặt khác, hai vectơ →OB và →OD có cùng giá là đường thẳng BD
Do đó, hai vectơ →OB và →OD cùng phương, mà chúng ngược hướng (2)
Từ (1) và (2) ta kết luận: →OB = –→OD.
Câu 7:
15/07/2024Cho hình vuông ABCD có tâm O. Các điểm Q, K, L, N lần lượt là trung điểm của AB, BC, CD, DA như hình vẽ.
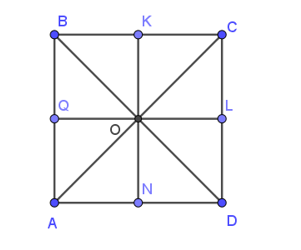
Khẳng định nào sau đây là đúng ?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C.
Xét hình vuông ABCD có:
BC // AD, do đó hai vectơ →KC và →AN cùng phương, mà chúng cùng hướng đi từ trái sang phải nên hai vectơ →KC và →AN cùng hướng (1).
Mặt khác: KC=12BC (do K là trung điểm của BC); AN=12AD (do N là trung điểm của AD).
Mà BC = AD (do ABCD là hình vuông)
⇒KC=AN⇒|→KC|=|→AN| (2)
Từ (1) và (2) suy ra →KC=→AN.
Câu 8:
14/07/2024Cho hình vuông ABCD có tâm O. Các điểm Q, K, L, N lần lượt là trung điểm của AB, BC, CD, DA như hình vẽ.
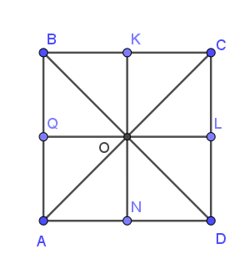
Khẳng định nào sau đây là sai ?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A.
Xét hình vuông ABCD có: Q là trung điểm của AB và L là trung điểm của CD.
Nên QL là đường trung bình của hình vuông ABCD.
Suy ra: BC //= QL và QL đi qua tâm O của hình vuông.
Do đó: →OQ và →KC cùng phương, mà chúng có hướng ngược nhau nên hai vectơ →OQ và →KC ngược hướng (1).
Mà: KC=12BC; OQ=12QL; BC = QL.
⇒KC=OQ⇒|→KC|=|→OQ| (2)
Từ (1) và (2) suy ra, →OQ=−→KC, vậy A sai.
Câu 9:
14/07/2024Cho hình thoi ABCD tâm I như hình vẽ với E, F, G, H lần lượt là trung điểm của các cạnh AB, AD, CD, CB.
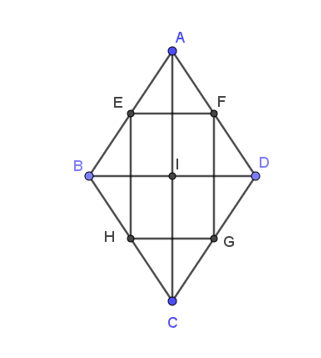
Khẳng định nào sau đây là đúng ?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B.
Xét hình thoi ABCD có:
AB = CD
Mà E là trung điểm của AB nên BE = 12AB
G là trung điểm của CD nên GD = 12CD
Do đó, BE = GD ⇒|→BE|=|→GD| (1)
Và: AB // CD
Do đó, →BE, →GD cùng phương, hơn nữa chúng cùng hướng (2).
Từ (1) và (2) suy ra →BE= →GD.
Câu 10:
21/07/2024Cho hình thoi ABCD tâm I như hình vẽ với E, F, G, H lần lượt là trung điểm của các cạnh AB, AD, CD, CB và J, L, K, M lần lượt là giao điểm của HE với BD, EF với AC, FG với BD, GH với AC.
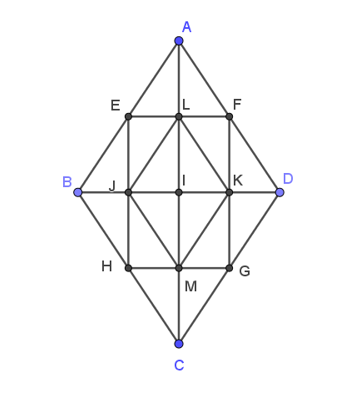
Khẳng định nào sau đây là sai ?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A.
Xét tam giác ABD có:
AB = AD (do ABCD là hình thoi)
Do đó, tam giác ABD cân tại A.
E là trung điểm của AB
F là trung điểm của AD
Do đó, EF là đường trung bình của tam giác ABD.
Lại có AI là đường cao của tam giác cân ABD (do I là giao hai đường chéo của hình thoi nên AC vuông góc với BD tại I)
Mà EF cắt AI tại L.
Từ đó ta suy ra L là trung điểm của AI.
Xét tam giác BAC có:
BA = BC (do ABCD là hình thoi)
Do đó, tam giác BAC cân.
E là trung điểm của AB
H là trung điểm của BC
Do đó, EH là đường trung bình của tam giác BAC.
Tương tự, BI là đường cao của tam giác BAC.
Mà EH cắt BI tại J
Từ đó suy ra J là trung điểm của BI.
Xét tam giác AIB có:
J là trung điểm của BI
L là trung điểm của AI
Do đó, JL là đường trung bình của tam giác AIB
⇒JL=12AB (1), JL // AB (2)
Xét hình thoi ABCD có:
AB = CD (3)
AB // CD (4)
Do G là trung điểm của CD nên ta có: GD=12CD (5)
Từ (1), (3), (5) ta suy ra: JL = GD nên |→JL|=|→GD| (6)
Từ (2), (4) và (6) ta suy ra: →JL=→GD (do chúng cùng phương, cùng hướng và có độ dài bằng nhau).
Vậy A sai.