Đại lượng y tỉ lệ nghịch với đại lượng x theo hệ số tỉ lệ a (a ≠ 0)

ta có x.y = a

$\Rightarrow$đại lượng x tỉ lệ nghịch với đại lượng y theo hệ số tỉ lệ là a.

Do $\frac{-2}{3}<0$ nên để $\mathrm{y}=\frac{-2}{3}\mathrm{x}$ nhận giá trị dương thì x < 0

Gọi số người tổ I, II, III lần lượt là

x, y, z ( người, x, y, z $\in \mathrm{N}*$ )

Theo đề bài ta có: x + y + z = 37

Năng suất lao động như nhau nên số công nhân và thời gian làm việc là hai đại lượng tỉ lệ nghịch

Do đó:

$$\begin{gathered} 12\mathrm{x}=10\mathrm{y}=8\mathrm{z} \\ \iff \frac{12\mathrm{x}}{120}=\frac{10\mathrm{y}}{120}=\frac{8\mathrm{z}}{120} \\ \iff \frac{\mathrm{x}}{10}=\frac{\mathrm{y}}{12}=\frac{\mathrm{z}}{15} \end{gathered}$$

Áp dụng tính chất của dãy tỉ số bằng nhau:

$$\begin{gathered} \frac{\mathrm{x}}{10}=\frac{\mathrm{y}}{12}=\frac{\mathrm{z}}{15} \\ =\frac{\mathrm{x}+\mathrm{y}+\mathrm{z}}{10+12+15}=\frac{37}{37}=1 \end{gathered}$$

Suy ra x = 10; y = 12; z = 15

Vậy số công nhân tổ II là 12 (công nhân)

Ta có: $\mathrm{y}=2\left|\mathrm{x}\right|=\left\{\begin{array}{l}2\mathrm{x}\\ -2\mathrm{x}\end{array}\mathrm{khi} \left\{\begin{array}{l}\mathrm{x}\ge 0\\ \mathrm{x}<0\end{array}\right.\right.$

Với $\mathrm{x}\ge 0$ thì y = 2x có đồ thị là tia OM với M (1; 2)

Với x <0 thì x = -2x có đồ thị là tia ON với N (-1; 2)

Vậy đồ thị hàm số $\mathrm{y}=2\left|\mathrm{x}\right|$ gồm hai tia OM thuộc góc phần tư thứ nhất và ON thuộc góc phần tư thứ hai

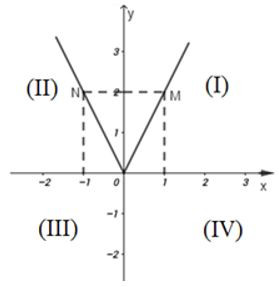
Hay đồ thị hàm số y = 2|x| gồm hai tia chung gốc O, thuộc góc phần tư thứ (I) và thứ (II)

Nếu M có hoành độ là −1 thì tung độ của điểm M là

y = −3.(−1) = 3.

Nếu NN có tung độ là 2 thì hoành độ của điểm N thỏa mãn

2 = −3.x ⇒ $\mathrm{x}=\frac{-2}{3}$

Do M, N thuộc đồ thị hàm số y = −3x nên đường thẳng MN đi qua gốc tọa độ O

Do điểm A (a; −0,2) thuộc đồ thị hàm số:

y = 4x nên ta có :

−0,2 = 4.a ⇒ a = −0,2:4 = −0,05

Gọi số máy cày của đội thứ nhất, đội thứ hai và đội thứ ba lần lượt là:

$\mathrm{x}, \mathrm{y}, \mathrm{z} \left(\mathrm{x}, \mathrm{y}, \mathrm{z}\in \mathrm{N}*\right)$

Cùng cày thửa ruộng như nhau và năng suất các máy như nhau thì số máy cày và thời gian cày là hai đại lượng tỉ lệ nghịch.

Do đó x, y, z tỉ lệ nghịch với 2, 3, 4 và x − z = 3.

Ta có:

$$\begin{gathered} 2\mathrm{x}=3\mathrm{y}=4\mathrm{z}\Rightarrow \frac{2\mathrm{x}}{12}=\frac{3\mathrm{y}}{12}=\frac{4\mathrm{z}}{12} \\ \Rightarrow \frac{\mathrm{x}}{6}=\frac{\mathrm{y}}{4}=\frac{\mathrm{z}}{3}=\frac{\mathrm{x}-\mathrm{z}}{6-3}=\frac{3}{3}=1 \end{gathered}$$

Do đó:

$$\begin{gathered} \frac{\mathrm{x}}{6}=1\Rightarrow \mathrm{x}=6 \\ \frac{\mathrm{y}}{4}=1\Rightarrow \mathrm{y}=4 \\ \frac{\mathrm{z}}{3}=1\Rightarrow \mathrm{z}=3 \end{gathered}$$

Vậy số máy cày của đội thứ nhât, đội thứ hai và đội thứ ba thứ tự là 6, 4, 3 máy.

Gọi ba phần cần tìm là x,y,z (x,y,z > 0)

Vì x, y, z tỉ lệ nghịch với $\frac{2}{3}; \frac{5}{4}$ và 2 nên ta có:

$\frac{2}{3}\mathrm{x}=\frac{5}{4}\mathrm{y}=2\mathrm{z}$

Do đó:

$$\begin{gathered} \frac{2\mathrm{x}}{3}=\frac{5\mathrm{y}}{4}=\frac{2\mathrm{z}}{1} \\ \iff \frac{2\mathrm{x}}{3.10}=\frac{5\mathrm{y}}{4.10}=\frac{2\mathrm{z}}{1.10} \\ \iff \frac{\mathrm{x}}{15}=\frac{\mathrm{y}}{8}=\frac{\mathrm{z}}{5} \end{gathered}$$

Mà tổng ba phần là 1316 nên ta có:

x + y + z =1316

Theo tính chất dãy tỉ số bằng nhau :

$$\begin{gathered} \frac{\mathrm{x}}{15}=\frac{\mathrm{y}}{8}=\frac{\mathrm{z}}{5} \\ =\frac{\mathrm{x}+\mathrm{y}+\mathrm{z}}{15+8+5}=\frac{1316}{28}=47 \end{gathered}$$

Suy ra:

x = 15.47 = 705;

y = 8.47 = 376

z = 5.47 = 235

Vậy phần lớn nhất là 705

Thay x = 2 vào f(x) ta được:

f(2) = -2.2 + 2 = -4 + 2 = -2

Thay x = 4 vào g(x) ta được

g(4) = 3.4 + 1 = 13

Do đó:

P = 2f(2) - 3g(4) = 2.(-2) - 2.13

P = -4 - 39 = -43

Vậy P = -43

Gọi số giấy vụn thu được của các lớp 7A1, 7A2, 7A3 lần lượt là:

x, y, z (kg, x, y, z > 0)

Theo đề bài ra, ta có:

$$\begin{gathered} \frac{\mathrm{x}}{{\displaystyle \frac{1}{4}}}=\frac{\mathrm{y}}{{\displaystyle \frac{1}{6}}}=\frac{\mathrm{z}}{{\displaystyle \frac{1}{5}}} \\ \mathrm{x}+\mathrm{y}+\mathrm{z}=370 \end{gathered}$$

Áp dụng tính chất của dãy tỉ số bằng nhau

$$\begin{gathered} \frac{\mathrm{x}}{{\displaystyle \frac{1}{4}}}=\frac{\mathrm{y}}{{\displaystyle \frac{1}{6}}}=\frac{\mathrm{z}}{{\displaystyle \frac{1}{5}}} \\ =\frac{\mathrm{x}+\mathrm{y}+\mathrm{z}}{{\displaystyle \frac{1}{4}}+{\displaystyle \frac{1}{6}}+{\displaystyle \frac{1}{5}}} \\ =\frac{370}{{\displaystyle \frac{15+10+12}{60}}} \\ =\frac{370}{{\displaystyle \frac{37}{60}}}=600 \\ \left\{\begin{array}{l}\mathrm{x}=600.\frac{1}{4}=150 \mathrm{kg}\\ \mathrm{y}=600.\frac{1}{6}=100 \mathrm{kg}\\ \mathrm{z}=600.\frac{1}{5}=120\mathrm{kg}\end{array}\right. \end{gathered}$$

Vậy số giấy vụn thu được của lớp 7A2 là 100kg

Điểm A (−3; 2) thuộc đồ thị hàm số y = ax+b nên ta có: 

2 = −3a+b ⇔ b = 2+3a (1) 
Điểm B (1; 4)  thuộc đồ thị hàm số y = ax+b nên ta có 

4 = a.1+b ⇔ b = 4−a (2)

Từ (1) và (2) ta có:

2+3a = 4−a ⇔ 3a+a = 4−2

⇔ 4a = 2 ⇔ $\mathrm{a}=\frac{1}{2}$

Với  $\mathrm{a}=\frac{1}{2}$ thì $\mathrm{b}=4-\mathrm{a}=4-\frac{1}{2}=\frac{7}{2}$

Vậy $\mathrm{a}=\frac{1}{2}; \mathrm{b}=\frac{7}{2}$

Thay các đáp án ta thấy $\mathrm{f}\left(\frac{1}{2}\right)=-2.\frac{1}{2}=-1\ne 2$ 

Thay x = 5 vào $\mathrm{y}=\frac{50}{\mathrm{x}}$ ta được $\mathrm{y}=\frac{50}{5}=10$

Vậy x = 10

Hoành độ x của giao điểm phải thỏa mãn điều kiện: $9\mathrm{x}=\frac{1}{\mathrm{x}}\left(\mathrm{x}\ne 0\right)$

Hay

$$\begin{gathered} 9\mathrm{x}.\mathrm{x}=1\iff 9{\mathrm{x}}^2=1 \\ \iff {\mathrm{x}}^2=\frac{1}{9}\Rightarrow \mathrm{x}=\pm \frac{1}{3} \end{gathered}$$

Với $\mathrm{x}=\frac{1}{3}\Rightarrow \mathrm{y}=9\mathrm{x}=9.\frac{1}{3}=3$

nên tọa độ giao điểm là $\left(\frac{1}{3}; 3\right)$

Với $\mathrm{x}=-\frac{1}{3}\Rightarrow \mathrm{y}=9\mathrm{x}=9.\left(-\frac{1}{3}\right)=-3$ 

nên tọa độ giao điểm là $\left(-\frac{1}{3}; -3\right)$

Vậy có hai giao điểm là: $\left(\frac{1}{3}; 3\right); \left(-\frac{1}{3}; -3\right)$

Ta có: $\frac{\mathrm{x}}{\mathrm{y}}=4\Rightarrow \mathrm{x}=4\mathrm{y}$

Thay vào biểu thức xy = 9 ta có

$$\begin{gathered} 4\mathrm{y}.\mathrm{y}=9\iff {\mathrm{y}}^2=\frac{9}{4} \\ \iff \left\{\begin{array}{l}\mathrm{y}=\frac{3}{2}\\ \mathrm{y}=-\frac{3}{2}\end{array}\right. \end{gathered}$$

+ Với $\mathrm{y}=\frac{3}{2}\Rightarrow \mathrm{x}=4.\frac{3}{2}=6 \left(\mathrm{tm}\right)$

+ Với $\mathrm{y}=-\frac{3}{2}\Rightarrow \mathrm{x}=4.\left(\frac{-3}{2}\right)=-6$

(ktm do $\mathrm{x}\ge 0$)

Vậy $\left(\mathrm{x}; \mathrm{y}\right)=\left(6; \frac{3}{2}\right)$

Số mét dây thép và cân nặng của dây thép là hai đại lượng tỉ lệ thuận.

Gọi cân nặng của 100m dây thép là x (gam)

( x > 75)

Khi đó áp dụng tính chất của tỉ lệ thuận ta có:

$\frac{6}{75}=\frac{100}{\mathrm{x}}\Rightarrow \mathrm{x}=\frac{100.75}{6}=1250$ (gam).

Vậy để bán 100m dây thép thì người bán cần phải cân cho khách hàng 1250 gam dây thép.

Do x và y là hai đại lượng tỉ lệ thuận nên ta có: 

$\mathrm{y}=\mathrm{kx}\Rightarrow \mathrm{k}=\frac{\mathrm{y}}{\mathrm{x}}=\frac{3}{-2}=\frac{-3}{2}$

Ta có: y tỉ lệ nghịch với x theo hệ số tỉ lệ là 2 nên $\mathrm{y}=\frac{2}{\mathrm{x}}$

z tỉ lệ nghịch với y theo hệ số tỉ lệ là 3 nên $\mathrm{z}=\frac{3}{\mathrm{y}}$

Do đó: $\mathrm{z}=\frac{3}{\mathrm{y}}=3:\frac{2}{\mathrm{x}}=\frac{3\mathrm{x}}{2}$

Vậy z và x tỉ lệ thuận với nhau và hệ số tỉ lệ là $\frac{3}{2}$

Thay tọa độ điểm M (−2; 3) vào hàm số

 y = x + 3 ta được: 

3 = −2 + 3 ⇒ 3 = 1 (vô lý).

Do đó M không thuộc đồ thị hàm số

y = x + 3y = x + 3

x và y là hai đại lượng tỉ lệ thuận nên $\frac{{\mathrm{y}}_1}{{\mathrm{x}}_1}=\frac{{\mathrm{y}}_2}{{\mathrm{x}}_2}$

Do đó:

$$\begin{gathered} \frac{{\mathrm{y}}_1}{{\mathrm{y}}_2}=\frac{{\mathrm{x}}_1}{{\mathrm{x}}_2}=\frac{2{\mathrm{y}}_1}{2{\mathrm{y}}_2} \\ =\frac{3{\mathrm{x}}_1}{3{\mathrm{x}}_2}=\frac{2{\mathrm{y}}_1+3{\mathrm{x}}_1}{2{\mathrm{y}}_2+3{\mathrm{x}}_2} \end{gathered}$$

(theo tính chất dãy tỉ số bằng nhau)

Hay:

$$\begin{gathered} \frac{{\mathrm{y}}_1}{3}=\frac{{\mathrm{x}}_1}{-6}=\frac{2{\mathrm{y}}_1+3{\mathrm{x}}_1}{2.3+3.\left(-6\right)} \\ =\frac{20}{-12}=\frac{-5}{3}\left(\mathrm{vì} 2{\mathrm{y}}_2+3{\mathrm{x}}_2=20\right) \end{gathered}$$

Từ đó: ${\mathrm{x}}_1=\left(-6\right).\left(\frac{-5}{3}\right)=10; {\mathrm{y}}_1=-5$

Vậy ${\mathrm{x}}_1=10; {\mathrm{y}}_1=-5$

Do M (1;−2) thuộc đồ thị hàm số y = ax nên:

−2 = 1.a ⇔ a = −2 ⇒ y = −2x−2 = 1

Người thứ nhất đánh được số trang là:

16.3 = 48 (trang)

Người thứ hai đánh được số trang là:

12.5 = 60 (trang)

Người thứ ba đánh được số trang là:

14.4 = 56 (trang)

Gọi x, y, z (x, y, z > 0) lần lượt là số tiền tính theo USD mà người thứ nhất, người thứ hai, người thứ ba nhận được

Theo đề bài ta có:

$$\begin{gathered} \frac{\mathrm{x}}{48}=\frac{\mathrm{y}}{60}=\frac{\mathrm{z}}{56} \\ \mathrm{x}+\mathrm{y}+\mathrm{z}=41 \end{gathered}$$

Áp dụng tính chất của dãy tỉ số bằng nhau:

$$\begin{gathered} \frac{\mathrm{x}}{48}=\frac{\mathrm{y}}{60}=\frac{\mathrm{z}}{56} \\ =\frac{\mathrm{x}+\mathrm{y}+\mathrm{z}}{48+60+56} \\ =\frac{41}{164}=\frac{1}{4} \end{gathered}$$

Suy ra:

$$\begin{gathered} \mathrm{x}=\frac{1}{4}.48=12; \\ \mathrm{y}=\frac{1}{4}.60=15; \\ \mathrm{z}=\frac{1}{4}.56=14 \end{gathered}$$

Suy ra người thứ nhất, người thứ hai, người thứ ba nhận được số tiền lần lượt là 12, 15, 14 (USD)

Người thứ ba nhận được 14 USD

 Ba số x, y, z tỉ lệ thuận với 3; 5; 7 nên theo tính chất về tỉ lệ thuận ta có: $\frac{\mathrm{x}}{3}=\frac{\mathrm{y}}{5}=\frac{\mathrm{z}}{7}$

Theo bài ra ta có z−y=10

Áp dụng tính chất dãy tỉ số bằng nhau, ta được: 

$$\begin{gathered} \frac{\mathrm{x}}{3}=\frac{\mathrm{y}}{5}=\frac{\mathrm{z}}{7} \\ =\frac{\mathrm{z}-\mathrm{y}}{7-5}=\frac{10}{2}=5 \end{gathered}$$

Nên x = 5.3 = 15

y = 5.5 = 25

z = 5.7 = 35

Vậy x = 15; y = 25; z = 35.