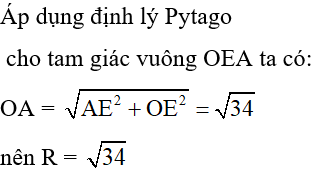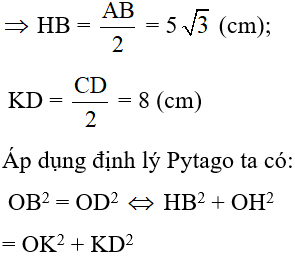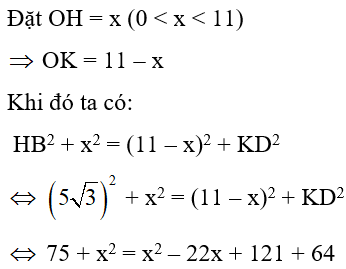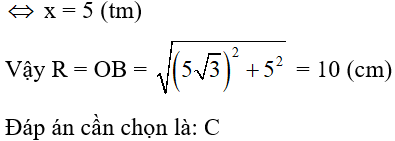Trắc nghiệm Toán 9 Bài 3: Liên hệ giữa dây và khoảng cách từ tâm đến dây
-
425 lượt thi
-
20 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
22/07/2024Cho đường tròn (O) có hai dây AB, CD không đi qua tâm. Biết khoảng cách từ tâm đến hai dây là bằng nhau. Kết luận nào sau đây là đúng?
Xem đáp án
Trong một đường tròn, hai dây cách đều tâm thì bằng nhau
Đáp án cần chọn là: B
Câu 2:
23/07/2024Cho đường tròn (O) có bán kính R = 5cm. Khoảng cách từ tâm đến dây AB là 3cm. Tính độ dài dây AB.
Xem đáp án
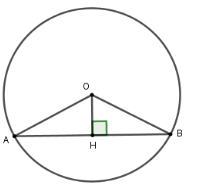
Kẻ OHAB tại H suy ra H là trung điểm AB
Xét tam giác OHB vuông tại H
có OH = 3cm;OB = 5cm.
Theo định lý Pytago ta có:
HB = = 4
Mà H là trung điểm của AB
nên AB = 2HB = 8cm
Vậy AB = 8cm
Đáp án cần chọn là: B
Câu 3:
21/07/2024Chọn khẳng định đúng trong các khẳng định sau. Trong hai dây của một đường tròn.
Xem đáp án
- Trong một đường tròn:
+ Hai dây bằng nhau thì cách đều tâm
- Trong hai dây của một đường tròn:
+ Dây nào lớn hơn thì dây đó gần tâm hơn
+ Dây nào gần tâm hơn thì dây đó lớn hơn
Nên phương án A, B, C sai; D đúng
Đáp án cần chọn là: D
Câu 5:
20/07/2024Chọn khẳng định sai trong các khẳng định sau. Trong hai dây của một đường tròn.
Xem đáp án
- Trong một đường tròn:
+ Hai dây bằng nhau thì cách đều tâm
- Trong hai dây của một đường tròn:
+ Dây nào lớn hơn thì dây đó gần tâm hơn
+ Dây nào gần tâm hơn thì dây đó lớn hơn
Nên phương án B, C, D đúng
Đáp án cần chọn là: A
Câu 7:
22/07/2024Cho đường tròn (O) có bán kính R = 6,5cm. Khoảng cách từ tâm đến dây AB là 2,5cm. Tính độ dài dây AB.
Xem đáp án
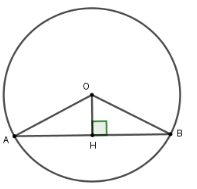
Kẻ OHAB tại H suy ra H là trung điểm AB
Xét tam giác OHB vuông tại H
có OH = 2,5cm; OB = 6,5cm.
Theo định lý Pytago ta có:
HB = = 6
Mà H là trung điểm của AB
nên AB = 2HB = 12cm
Vậy AB = 12cm
Đáp án cần chọn là: D
Câu 8:
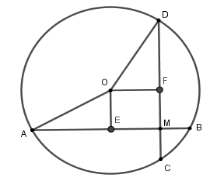
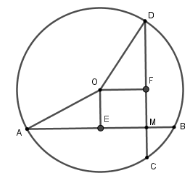
23/07/2024Cho đường tròn (O; R) có hai dây AB, CD bằng nhau và vuông góc với nhau tại I. Giả sử IA = 2cm; IB = 4cm. Tổng khoảng cách từ tâm O đến dây AB, CD là:
Xem đáp án
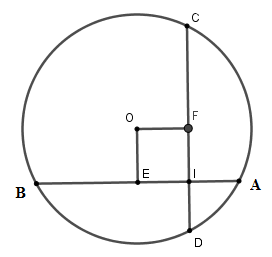
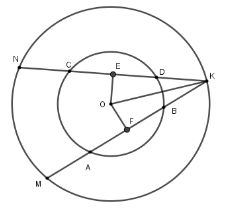
Xét đường tròn tâm (O).
Kẻ OEAB tại E suy ra E là trung điểm của AB,
kẻ OFCD tại F.
Vì dây AB = AC nên OE = OF
(hai dây bằng nhau cách đều tâm)
Xét tứ giác OEIF có = 90o
nên OEIF là hình chữ nhật và OE = OF
nên OEIF là hình vuông
OE = OF = EI
Mà AB = IA + IB = 6cm
EB = 3cm EI = EB – IB = 1cm
nên OE = OF = 1cm
Vậy tổng khoảng cách từ tâm đến hai dây là AB, CD là 2cm
Đáp án cần chọn là: D
Câu 9:
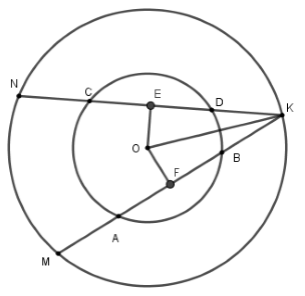
20/07/2024Cho đường tròn (O; 8cm). Dây AB và CD song song, có độ dài lần lượt là 14cm và 10cm. Tính khoảng cách giữa 2 dây.
Xem đáp án
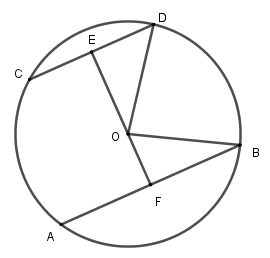
Kẻ đường thẳng qua O vuông góc với CD tại E và cắt AB tại F thì EF AB vì AB // CD
Khi đó E là trung điểm của CD và F là trung điểm của AB (đường kính vuông góc với dây thì đi qua trung điểm dây đó).
Nên ED = = 5cm;
FB = = 7cm; OD = OB = 8cm
Áp dụng định lý Pytago cho tam giác vuông OED ta được:
OE = cm
Áp dụng định lý Pytago cho tam giác vuông OFB ta được:
OF = cm
Vậy khoảng cách giữa hai dây
là EF = OE + OF =(cm)
Đáp án cần chọn là: D
Câu 10:
23/07/2024Cho đường thẳng d cắt đường tròn (O) tại hai điểm phân biệt A, B. Biết khoảng cách từ điểm O đến đường thẳng d bằng 3cm và độ dài đoạn thẳng AB bằng 8cm. Bán kính của đường tròn (O) bằng:
Xem đáp án
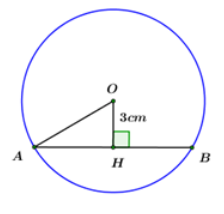
Kẻ OHAB. Khi đó H là trung điểm của AB (mối liên hệ giữa đường kính và dây cung)
Áp dụng định lý Pytago cho AOH vuông tại H ta có:
OA2 = AH2 + HO2 = 42 + 32 = 25
R = OA = 5cm
Đáp án cần chọn là: D
Câu 12:
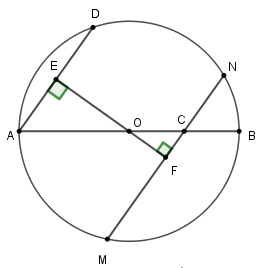
18/07/2024Cho đường tròn (O), đường kính AB. Kẻ hai dây AC và BD song song. So sánh độ dài AC và BD
Xem đáp án
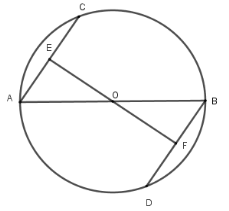
Kẻ đường thẳng qua O vuông góc với A tại E và cắt BD tại F thì EFBD tại F vì AC // BD.
Xét hai tam giác vuông OEA và tam giác OFB
có OB = OA; (so le trong)
Nên (ch-gn)
AC = DB
(hai dây cách đều tâm thì bằng nhau)
Đáp án cần chọn là: C
Câu 15:
19/07/2024Cho đường tròn (O; R) có hai dây AB, CD bằng nhau và vuông góc với nhau tại I. Giả sử IA = 6cm; IB = 3cm. Tổng khoảng cách từ tâm O đến dây AB, CD là:
Xem đáp án
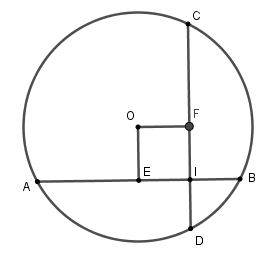
Xét đường tròn tâm (O)
Kẻ OEAB tại E suy ra E là trung điểm của AB,
kẻ OFCD tại F.
Vì dây AB = AC nên OE = OF
(hai dây bằng nhau cách đều tâm)
Xét tứ giác OEIF có = 90o
nên OEIF là hình chữ nhật và OE = OF
nên OEIF là hình vuôngOE = OF = EI
Mà AB = IA + IB = 9cmEB = 4,5cm
EI = EB – IB = 1,5cm
nên OE = OF = 1,5cm
Vậy tổng khoảng cách từ tâm đến hai dây
là AB, CD là 1,5 + 1,5 = 3cm
Đáp án cần chọn là: C
Câu 16:
21/07/2024Cho đường tròn (O; 10cm). Dây AB và CD song song, có độ dài lần lượt là 16cm và 12cm. Tính khoảng cách giữa 2 dây.
Xem đáp án
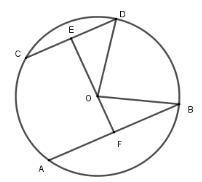
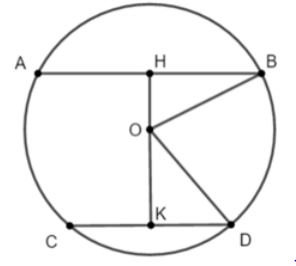
Kẻ đường thẳng qua O vuông góc với CD tại E
và cắt DB tại F thì EF AB vì AB // CD
Khi đó E là trung điểm của CD và F là trung điểm của AB (đường kính vuông góc với dây thì đi qua trung điểm dây đó). Nên ED = 6cm; FB = 8cm; OD = OB= 10cm
Áp dụng định lý Pytago cho tam giác vuông OED ta được:
OE = = 8cm
Áp dụng định lý Pytago cho tam giác vuông OFB ta được:
OF = = 6cm
Vậy khoảng cách giữa hai dây là:
EF = OE + OF = 14cm
Đáp án cần chọn là: A
Câu 17:
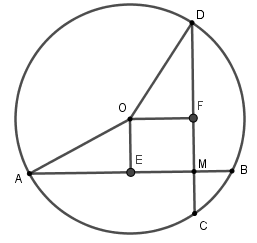
20/07/2024Cho đường tròn (O; R) có hai dây AB, CD vuông góc với nhau ở M. Biết CD = 8cm; MC = 1cm. Khoảng cách từ tâm O đến dây AB là?
Xem đáp án
Kẻ OEAB tại E
suy ra E là trung điểm của AB,
kẻ OFCD tại F suy ra F là trung điểm CD
Xét tứ giác OEMF có
nên OEIF là hình chữ nhật, suy ra FM = OE
Ta có CD = 8cmFC = 4cm
mà MC = 1cmFM = FC –MC = 4 – 1 = 3cm
nên OE = FM = 3cm
Vậy khoảng cách từ tâm O đến dây AB là 3cm
Đáp án cần chọn là: C
Câu 20:
15/07/2024Cho đường tròn (O) có hai dây AB, CD không đi qua tâm. Biết khoảng cách từ tâm O đến dây AB lớn hơn khoảng cách từ tâm O đến dây CD. Kết luận nào sau đây là đúng?
Xem đáp án
Trong một đường tròn: Dây nào gần tâm hơn thì dây đó lớn hơn
Từ đề bài ta thấy dây CD gần tâm hơn dây AB nên AC > AB
Đáp án cần chọn là: C