Giải SGK Hoạt động trải nghiệm 4 CTST Tuần 3
Giải SGK Hoạt động trải nghiệm 4 CTST Tuần 3
-
139 lượt thi
-
30 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 3:
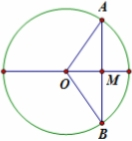
22/07/2024Cho mặt cầu (S) tâm O, bán kính bằng 2 và mặt phẳng (P). Khoảng cách từ O đến (P) bằng 4. Từ điểm M thay đổi trên (P) kẻ các tiếp tuyến MA, MB, MC tới (S) với A, B, C là các tiếp điểm. Biết mặt phẳng (ABC) luôn đi qua một điểm I cố định. Tính độ dài đoạn OI.
 Xem đáp án
Xem đáp án
Đáp án D
Câu 9:
11/10/2024Cho hình trụ có thiết diện qua trục là hình vuông cạnh 2a. Mặt phẳng (P) song song với trục và cách trục một khoảng . Tính diện tích thiết diện của hình trụ cắt bởi (P)
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
*Phương pháp giải:
- nhận biết được thiết diện hình trụ cắt (P) chính là hình chữ nhật
- vẽ hình và tính từng cạnh của hình chữ nhật(thiết diện): do chiều dài sẽ bằng luôn cạnh hình vuông hay chính chiều cao hình trụ, nên chỉ tính chiều rộng là nằm dưới mặt đáy
*Lời giải:
Gọi thiết diện mặt cắt là hình vuông ABCD.
Xét mặt đáy tâm O như hình vẽ. Vì thiết diện qua trục là hình vuông cạnh 2a nên chiều cao của hình trụ OO' = 2a = BC và OA = a.
⇒AB=2√OA2−OM2=a√3
Diện tích thiết diện cần tính: AB.CD=2a2√3.
*Công thức tính thiết diện của hình trụ:
1. Cắt hình trụ bởi mặt phẳng (P) qua trục
- Thiết diện nhận được là một hình chữ nhật.
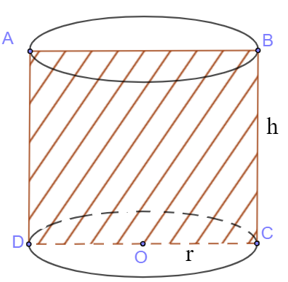
Diện tích thiết diện: SABCD = BC.CD =2r.h
2. Cắt hình trụ bởi mặt phẳng (P) song song và cách trục một khoảng x,
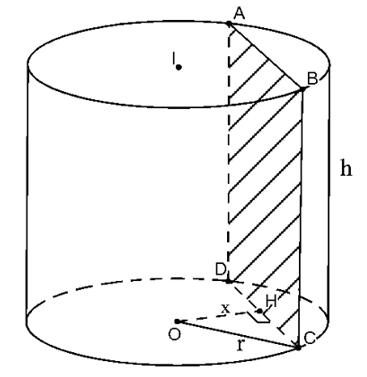
Thiết diện tạo thành là hình chữ nhật ABCD như hình trên.
Gọi H là trung điểm CD ta có OH ⊥ CD=> CD=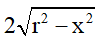
Do đó diện tích thiết diện SABCD =CD.BC= 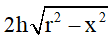
3. Cắt hình trụ bởi mặt phẳng (P) vuông góc với trục.
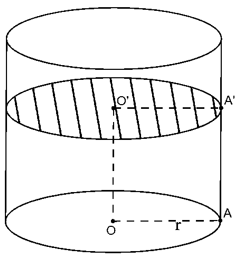
Thiết diện tạo thành là hình tròn tâm O’ bán kính O'A'=r
Diện tích thiết diện: S= πr2
4. Cắt hình trụ bởi mặt phẳng (P) không vuông góc với trục nhưng cắt tất cả các đường sinh của hình trụ.
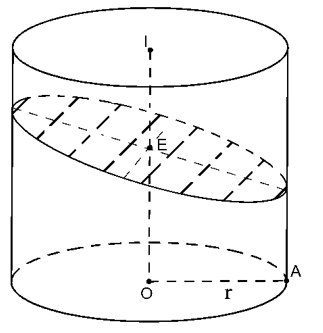
Thiết diện tạo thành là Elip (E) có trục nhỏ 2r => a=r
Trục lớn bằng 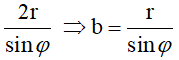 với
với 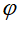 là góc giữa trục OI với (P)
là góc giữa trục OI với (P)
Do đó diện tích S= π. a.b= 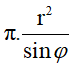
Xem thêm các bài viết liên quan hay, chi tiết
Bài toán về mặt trụ và phương pháp giải bài tập (có đáp án)
160 Bài tập Hình học không gian lớp 11 cơ bản, nâng cao có lời giải (P4)
Câu 12:
22/07/2024Cho quả địa cầu có độ dài đường kinh tuyến Đông là cm. Độ dài đường xích đạo là
 Xem đáp án
Xem đáp án
Đáp án C
Độ dài đường xích đạo gấp 2 lần độ dài đường kinh tuyến bất kì
Câu 27:
07/10/2024Tính thể tích V của khối lăng trụ tam giác đều có tất cả các cạnh bằng a.
 Xem đáp án
Xem đáp án
Đáp án đúng: A.
*Phương pháp giải:
- Lăng trụ tam giác đều là lăng trụ đứng có đáy là tam giác đều nên các cạnh bằng nhau và các góc bằng nhau
- Áp dụng công thức V = B.h trong đó B là diện tích tam giác đều cạnh a và h là chiều cao của lăng trụ
*Lời giải:
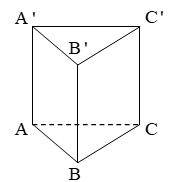
Đáy ABC là tam giác đều cạnh a nên có diện tích là :
Đường cao của hình lăng trụ: h = AA’ = a
Thể tích của khối lăng trụ là:
*Các dạng bài về hình lăng trụ đứng tam giác
a) Nhận biết các yếu tố của lăng trụ đứng tam giác, tứ giác
*Phương pháp: vẽ hình, quan sát để xác định các mặt, các cạnh, các đỉnh.Để vẽ hình lăng trụ đứng, ta thường vẽ một đáy, sau đó vẽ các cạnh bên là các đoạn thẳng song song và bằng nhau.
b) Tính diện tích, thể tích của hình lăng trụ đứng tam giác, tứ giác
* lăng trụ đứng tam giác:
+ Diện tích xung quanh của hình lăng trụ đứng tam giác bằng tích của chu vi đáy với chiều cao của nó.
+ Diện tích toàn phần: Diện tích toàn phần bằng diện tích xung quanh cộng diện tích hai đáy.
+ Thể tích của hình lăng trụ đứng tam giác bằng diện tích đáy nhân với chiều cao.
* lăng trụ đứng tứ giác:
+ Diện tích xung quanh của hình lăng trụ đứng tứ giác bằng tích của chu vi đáy với chiều cao của nó.
+ Diện tích toàn phần: Diện tích toàn phần bằng diện tích xung quanh cộng diện tích hai đáy.
+ Thể tích của hình lăng trụ đứng tứ giác bằng diện tích đáy nhân với chiều cao.
Xem thêm các bài viết liên quan hay, chi tiết:
