Đề thi Toán 9 giữa kì 2 có đáp án (đề 5)
-
2202 lượt thi
-
11 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
21/07/2024Phương trình nào sau đây là phương trình bậc nhất hai ẩn?
Xem đáp án
Đáp án đúng là: B
Do phương trình bật nhất hai ẩn có dạng ax + by = c
Nên phương trình bậc nhất hai ẩn trong các phương trình trên là: x – 2y = 1
Câu 2:
22/07/2024Phương trình 10x2 + 5x – 16 = 0 có số nghiệm là:
Xem đáp án
Đáp án đúng là: B
Phương trình bậc hai một ẩn có a.c = 10.(−16) = −160 < 0 nên phương trình có hai nghiệm.
Câu 3:
23/07/2024Hệ phương trình có nghiệm là
Xem đáp án
Đáp án đúng là: A
Û
Û
Û
Û
Vậy hệ phương trình đã cho có nghiệm là (2; −3).
Câu 4:
21/07/2024Số đo của góc có đỉnh nằm bên trong đường tròn bằng
Xem đáp án
Đáp án đúng là: C
Số đo của góc có đỉnh nằm bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.
Câu 5:
21/07/2024Các góc nội tiếp chắn nửa đường tròn là
Xem đáp án
Đáp án đúng là: D
Góc nội tiếp chắn nửa đường tròn là góc vuông.
Câu 6:
22/07/2024Cho hình vẽ bên. Biết 110°, bán kính R = 3cm, độ dài cung BmC bằng
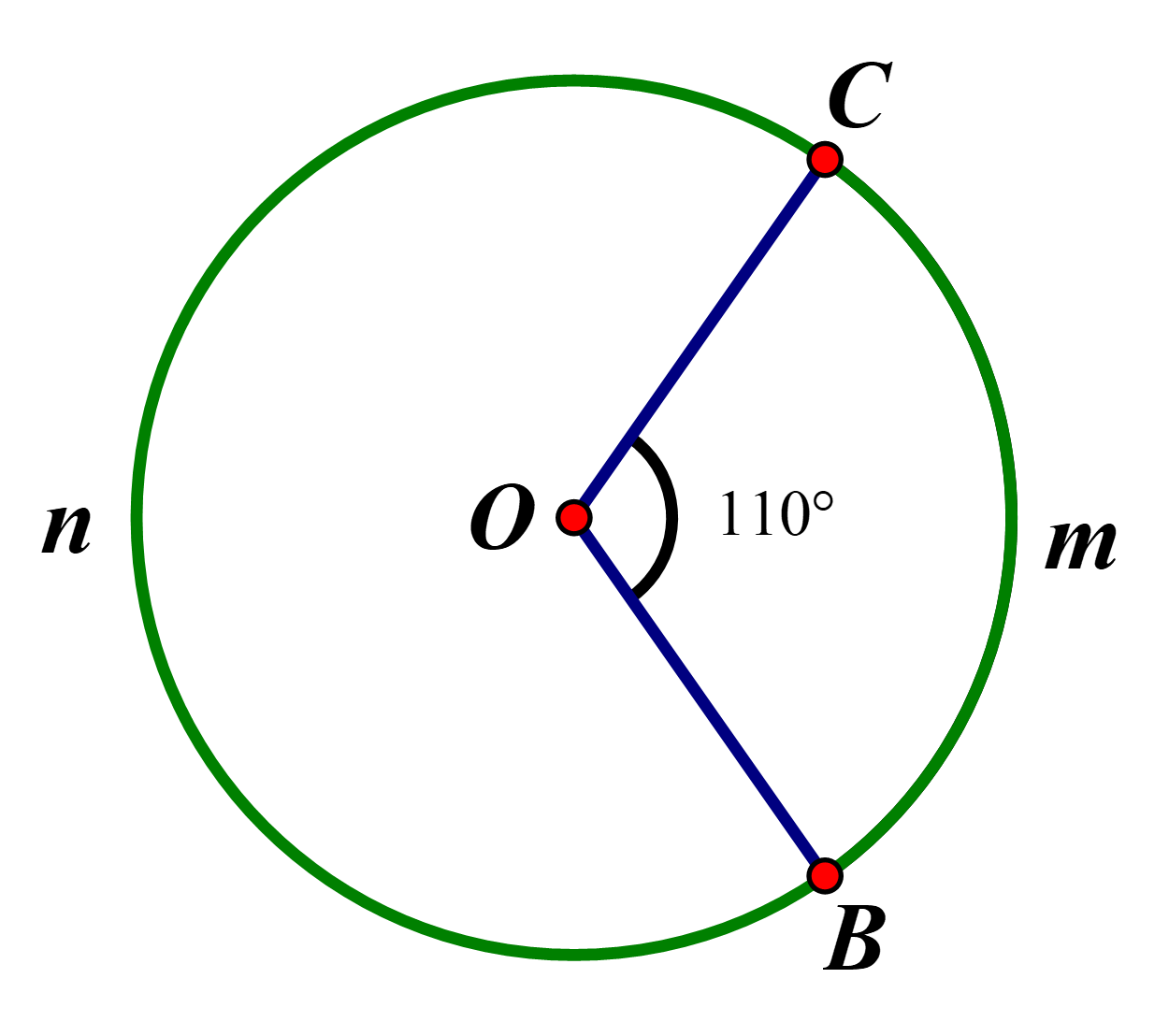
Xem đáp án
Đáp án đúng là: D
Độ dài cung BmC bằng: .
Câu 7:
21/07/2024Giải phương trình 3x2 – 11x + 6 = 0
Xem đáp án
Tính ∆ = b2 – 4ac. Phương trình có các hệ số là a = 3; b = −11; c = 6.
∆ = (−11)2 – 4.3.6 = 121 – 72 = 49 > 0
Do ∆ > 0, áp dụng công thức nghiệm, phương trình có hai nghiệm phân biệt:
x1 = ; x2 = .
Vậy phương trình có tập nghiệm là S =.
Câu 8:
21/07/2024a. Vẽ Parabol: (P): y = x2 và đường thẳng (d): y = 2x + 3 trên cùng mặt phẳng tọa độ
b. Tìm tọa độ giao điểm của (P) và (d) bằng phép tính
Xem đáp án
a. Vẽ (P)
Bảng giá trị:
|
x |
−2 |
−1 |
0 |
1 |
2 |
|
y = x2 |
4 |
1 |
0 |
1 |
4 |
Trên mặt phẳng tọa độ lấy các điểm A(−2; 4); B(−1; 1); O(0; 0); C(1; 1); D(2; 4).
Vẽ (d)
Đường thẳng (d): y = 2x + 3 có a = 2, b = 3 đi qua hai điểm (0; b) và
Do đó, hai điểm thuộc đường thẳng (d) là M(0; 3) và N(−1,5; 0).
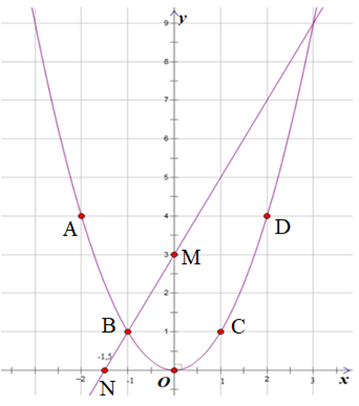
b. Phương trình hoành độ giao điểm của (P) và (d) là:
x2 = 2x + 3
Û x2 – 2x – 3 = 0
Û x2 – 3x + x – 3 = 0
Û x(x – 3) + (x – 3) = 0
Û (x – 3)(x + 1) = 0
Û
• Với x = 3 thì y = 2x + 3 = 2.3 + 3= 9.
Do đó, ta có tọa độ giao điểm của (P) và (d) là A(3; 9).
• Với x = −1 thì y = 2x + 3 = 2.(−1) + 3 = 1.
Do đó, ta có tọa độ giao điểm của (P) và (d) là B(−1; 1).
Vậy hai đồ thị hàm số trên có hai giao điểm là A(3; 9) và B(−1; 1).
Câu 9:
21/07/2024Giải bài toán bằng cách lập hệ phương trình
Một khu vườn hình chữ nhật có chu vi bằng 46m. Nếu tăng chiều dài 5m và giảm chiều rông 3m thì chiều dài gấp 4 lần chiều rộng. Tính diện tích khu vườn hình chữ nhật?
Xem đáp án
Gọi x (m) là chiều dài của khu vườn (x > 0)
y (m) là chiều rộng của khu vườn (y > 3)
Khu vườn hình chữ nhật có chu vi bằng 46m ta có: 2x + 2y = 46 (m) (1)
Chiều dài hình chữ nhật sau khi tăng 5 m là: x + 5 (m)
Chiều rộng hình chữ nhật sai khi giảm là: y – 3 (m)
Tăng chiều dài 5m và giảm chiều rông 3m thì chiều dài gấp 4 lần chiều rộng nên ta có phương trình: x + 5 = 4(y – 3) (2)
Từ (1) và (2), ta có hệ phương trình:
Û
Û
Û
Û (thỏa mãn)
Khi đó diện tích khu vườn là S = x.y = 15.8 = 120 (m2).
Vậy diện tích khu vườn hình chữ nhật là 120 m2.
Câu 10:
23/07/2024Cho nửa đường tròn (O) đường kính AB. Kẻ tiếp tuyến Bx với nửa đường tròn. Gọi C là điểm trên nửa đường tròn sao cho cung CB bằng cung CA, D là một điểm tùy ý trên cung CB (D khác C và B). Các tia AC, AD cắt Bx theo thứ tự tại E và F.
a. Chứng minh rằng: ∆ABE là tam giác cân
b. Chứng minh rằng: FB2 = FD.FA
c. Chứng minh rằng: CDFE là tứ giác nội tiếp
Xem đáp án
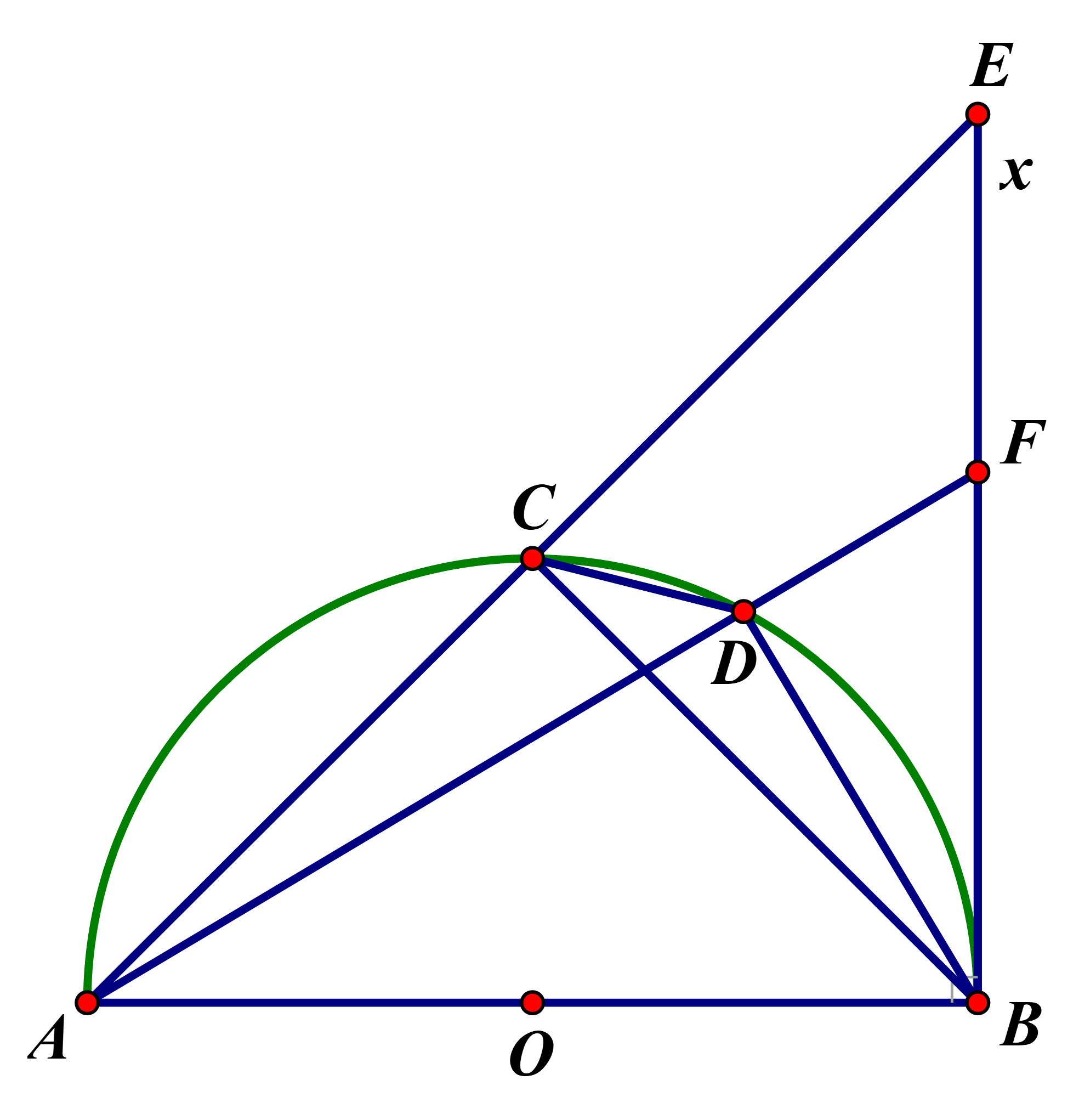
a. Ta có (hai góc nội tiếp chắn hai cung bằng nhau)
Ta lại có = 90° (góc nội tiếp chắn nửa đường tròn)
Suy ra tam giác CAB là tam giác vuông cân và = 45°
Xét tam giác ABE vuông tại B (Bx là tiếp tuyến của (O)) có = 45°
Dẫn đến = 180° − = 180 – 90 – 45 = 45° =
Suy ra tam giác ABE là tam giác vuông cân.
b. Xét ∆ FDB và ∆ FBA có:
là góc chung
= = 90° ( là góc nội tiếp chắn nữa đường tròn và Bx là tiếp tuyến của (O))
Suy ra ∆ FDB ∆ FBA (g.g)
Từ đó suy ra FB2 = FD.FA (đpcm)
c. Từ câu b ta suy ra được: Trong một tam giác vuông thì bình phương cạnh góc vuông bằng tích hình chiếu của nó trên cạnh huyền nhân với cạnh huyền.
Xét tam giác ABF vuông tại B đường cao BD ta có: AB2 = AD.AF
ABE vuông tại B đường cao BC ta có: AB2 = AC.AE
Suy ra AD.AF = AC.AE
Xét ∆ ACD và ∆ AFE có:
là góc chung
(chứng minh trên)
Suy ra ∆ ACD ∆ AFE (c.g.c)
Suy ra suy ra tứ giác CDFE là tứ giác nội tiếp.
Câu 11:
16/07/2024Cho hệ phương trình (I):
Xác định m để nghiệm (x0; y0) của hệ (I) thỏa điều kiện x0 + y0 = 1
Xem đáp án
Do (x0; y0) là nghiệm của hệ (I) nên ta có 2x0 – y0 = –2
Và x0 + y0 = 1 nên ta có hệ phương trình
Û
Û
Û
Û
Thay cặp nghiệm vào phương trình chứa m của hệ (I) ta được
Vậy m = −11 thỏa mãn bài toán.