Đề thi Giữa kì 1 Toán 10 Cánh diều có đáp án
Đề thi Giữa kì 1 Toán 10 Cánh diều có đáp án - Đề 2
-
488 lượt thi
-
30 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
22/07/2024Cho tập hợp A và a là một phần tử của tập hợp A. Trong các mệnh đề sau, mệnh đề nào sai?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có a là một phần tử của tập hợp A nên ta viết a ∈ A. Do đó C là mệnh đề đúng và B là mệnh đề sai.
Ta lại có {a} là tập con của tập A nên ta viết {a} ⊂ A. Do đó A là mệnh đề đúng.
Ngoài ra tập là tập con của tất cả các tập hợp nên ta có A. Do đó D là mệnh đề đúng.
Câu 2:
15/07/2024Cho mệnh đề chứa biến P(n): “n2 chia hết cho 4 ” với n là số nguyên. Chọn mệnh đề đúng trong các mệnh đề sau:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Với n = 5 ta có mệnh đề P(5): “52 chia hết cho 4 ”. Đây là mệnh đề sai vì 52 = 25 chia cho 4 dư 1.
Với n = 3 ta có mệnh đề P(3): “32 chia hết cho 4 ”. Đây là mệnh đề sai vì 32 = 9 chia cho 4 dư 1.
Với n = 2 ta có mệnh đề P(2): “22 chia hết cho 4 ”. Đây là mệnh đề đúng vì 22 = 4 chia hết cho 4.
Với n = 1 ta có mệnh đề P(1): “12 chia hết cho 4 ”. Đây là mệnh đề sai vì 12 = 1 chia cho 4 dư 1.
Câu 3:
15/07/2024Mệnh đề phủ định của mệnh đề “Phương trình ax2 + bx + c = 0 (a ≠ 0) vô nghiệm” là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có mệnh đề phủ định của mệnh đề “Phương trình ax2 + bx + c = 0 (a ≠ 0) vô nghiệm” là: Phương trình ax2 + bx + c = 0 (a ≠ 0) có nghiệm.
Câu 4:
22/07/2024Cho A = {0; 1; 2; 3; 4} và B = {2; 3; 4; 5; 6}. Tập hợp (A \ B) ∪ (B \ A) bằng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Ta có A \ B = {0; 1} và B \ A = {5; 6}.
Khi đó: (A \ B) ∪ (B \ A) = {0; 1; 5; 6}.
Câu 5:
20/07/2024Số phần tử của tập hợp A = {k2 + 1| k ∈ ℤ, |k| ≤ 2} bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có |k| ≤ 2
⇔ – k ≤ 2 hoặc k ≤ 2
⇔ k ≥ – 2 hoặc k ≤ 2
⇒ – 2 ≤ k ≤ 2
Mà k ∈ ℤ nên k ∈ {– 2; – 1; 0; 1; 2}.
⇒ k2 + 1 ∈ {1; 2; 5}.
Do đó A = {1; 2; 5}. Vì vậy tập hợp A có 3 phần tử.
Câu 6:
11/07/2024Cho hai tập hợp (1; 3) và [2; 4]. Giao của hai tập hợp đã cho là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta biểu diễn các tập hợp đã cho trên trục số ta được:
![Cho hai tập hợp (1; 3) và [2; 4]. Giao của hai tập hợp đã cho là (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2022/09/blobid3-1663923710.png)
Vì vậy (1; 3) ∩ [2; 4] = [2; 3).
Câu 7:
22/07/2024
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Từ việc quan sát vào hình vẽ ta thấy phần không bị gạch chéo biểu diễn cho tập hợp:
(– ∞; – 2) ∪ [5; +∞).
Câu 8:
12/07/2024Lớp 10A1 có 6 học sinh giỏi Toán, 4 học sinh giỏi Lý, 5 học sinh giỏi Hóa, 2 học sinh giỏi Toán và Lý, 3 học sinh giỏi Toán và Hóa, 2 học sinh giỏi Lý và Hóa, 1 học sinh giỏi cả 3 môn Toán, Lý, Hóa. Số học sinh giỏi ít nhất một môn (Toán, Lý, Hóa) của lớp 10A1 là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Gọi T là tập hợp các bạn học sinh giỏi Toán, khi đó |T| = 6;
L là tập hợp các bạn học sinh giỏi Lý, khi đó |L| = 4;
H là tập hợp các bạn học sinh giỏi Hóa, khi đó |H| = 5.
Do đó ta có:
T ∩ L là tập hợp các bạn học sinh vừa giỏi môn Toán vừa giỏi Lý nên |T ∩ L| = 2;
T ∩ H là tập hợp các bạn học sinh vừa giỏi môn Toán vừa giỏi Hóa nên |T ∩ H| = 3;
H ∩ L là tập hợp các bạn học sinh vừa giỏi môn Hóa vừa giỏi Lý nên |H ∩ L| = 2.
T ∩ L ∩ H là tập hợp các bạn học sinh vừa giỏi môn Toán vừa giỏi Lý và vừa giỏi Hóa nên |T ∩ L ∩ H | = 1.
Tập hợp số học sinh giỏi ít nhất một môn là T ∪ L ∪ H. Khi đó:
|T ∪ L ∪ H| = |T| + |L| + |H| – |T ∩ L| – |T ∩ H| – |H ∩ L| + |T ∩ L ∩ H |
= 6 + 4 + 5 – 2 – 3 – 2 + 1 = 9.
Vậy có 9 học sinh của lớp 10A1 vừa giỏi môn Toán vừa giỏi Lý và vừa giỏi Hóa.
Câu 9:
20/07/2024Cặp số (x; y) nào sau đây là nghiệm của bất phương trình 5x – 3y ≤ 2?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
+) Với (0; – 2) thay x = 0 và y = – 2 vào 5x – 3y ≤ 2 ta được:
5.0 – 3.(– 2) ≤ 2 ⇔ 6 ≤ 2 là một mệnh đề sai.
Do đó (0; – 2) không là nghiệm của bất phương trình.
+) Với (3; 0) thay x = 3 và y = 0 vào 5x – 3y ≤ 2 ta được:
5.3 – 3.0 ≤ 2 ⇔ 15 ≤ 2 là một mệnh đề sai.
Do đó (3; 0) không là nghiệm của bất phương trình.
+) Với (2; 1) thay x = 2 và y = 1 vào 5x – 3y ≤ 2 ta được:
5.2 – 3.1 ≤ 2 ⇔ 7 ≤ 2 là một mệnh đề sai.
Do đó (2; 1) không là nghiệm của bất phương trình.
+) Với (– 1; – 1) thay x = – 1 và y = – 1 vào 5x – 3y ≤ 2 ta được:
5.(– 1) – 3.(– 1) ≤ 2 ⇔ – 2 ≤ 2 là một mệnh đề đúng.
Do đó (– 1; – 1) không là nghiệm của bất phương trình.
Câu 10:
13/07/2024Bất phương trình nào sau đây không là bất phương trình bậc nhất một ẩn?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Ta thấy bất phương trình ở các đáp án A, B, C đều có dạng của bất phương trình bậc nhất hai ẩn.
Còn ý d là bất phương trình bậc 2. Do đó D không là bất phương trình bậc nhất một ẩn.
Câu 11:
22/07/2024Phần mặt phẳng không bị gạch chéo trong hình vẽ bên (kể cả biên) là biểu diễn hình học tập nghiệm của hệ bất phương trình nào dưới đây?
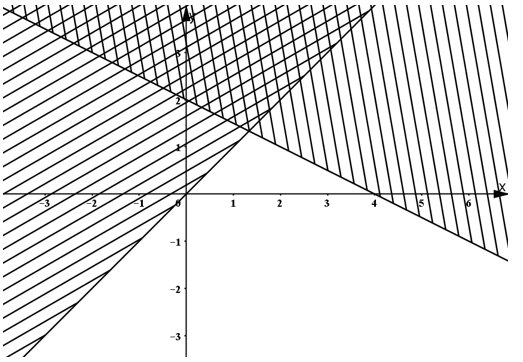
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Câu 12:
13/07/2024Cho sin35° ≈ 0,57. Giá trị của sin145° gần với giá trị nào nhất sau đây:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có 35° + 145° = 180°
⇒ sin35° = sin (180° – 145°) = sin145°
⇒ sin145° = sin35° ≈ 0,57.
Câu 13:
11/07/2024Tính giá trị biểu thức: A = cos 0° + cos 40° + cos 120° + cos 140°
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
A = cos 0° + cos 40° + cos 120° + cos 140°
= 1 + cos 40° – – cos 40°
=
![]() .
.
Câu 14:
21/07/2024Cho tam giác ABC, ta có các đẳng thức:
(I) sin = sin;
(II) tan = cot;
(III) sinA = sin(B + C).
Có bao nhiêu đẳng thức đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Xét tam giác ABC, ta có:
A + B + C = 1800 ⇒ A = - ( B + C)
⇒ sinA = sin(180°– (B + C)) = sin(B + C). Do đó (III) đúng.
⇒=
Câu 15:
13/07/2024Cho điểm M(x0; y0) nằm trên đường tròn đơn vị thỏa mãn xOM = . Khi đó phát biểu nào dưới đây là sai?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Điểm M(x0; y0) nằm trên đường tròn đơn vị thỏa mãn ![]() nên ta có:
nên ta có:
sinα = y0;
cosα = x0;
tanα =;
cotα =.
Do đó A là đáp án sai.
Câu 16:
21/07/2024Trong các công thức dưới đây, công thức nào sai về cách tính diện tích tam giác ABC? Biết AB = c, AC = b, BC = a, ha, hb, hc lần lượt là các đường cao kẻ từ đỉnh A, B, C, r là bán kính đường tròn nội tiếp, R là bán kính đường tròn ngoại tiếp tam giác ABC.
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Câu 17:
13/07/2024Cho tam giác ABC, có các cạnh AB = c, AC = b, BC = a. Định lí sin được phát biểu:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Xét tam giác ABC, định lí sin được phát biểu như sau:
Do đó B đúng.
Câu 18:
19/07/2024Cho tam giác ABC có BC = 50 cm, B = 65o C = 45o Tính chu vi của tam giác ABC (làm tròn kết quả đến hàng phần mười theo đơn vị xăng – ti – mét):
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Câu 19:
13/07/2024Một người đứng ở vị trí A trên nóc một ngôi nhà cao 8m đang quan sát một cây cao cách ngôi nhà 25m và đo được BAC =. Chiều cao của cây gần với kết quả nào nhất sau đây?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Câu 23:
17/07/2024Cho tam giác đều ABC có AB=a, M là trung điểm của BC. Khi đó bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Câu 24:
20/07/2024Cho hình bình hành ABCD. Mệnh đề nào sau đây đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Vì ABCD là hình bình hành nên AB // CD, AD // BC và AD = CD, AD = BC nên .
Câu 25:
18/07/2024Cho hình chữ nhật ABCD tâm O. Gọi M, N lần lượt là trung điểm của các cạnh AB, AD. Chọn khẳng định đúng trong các khẳng định sau:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
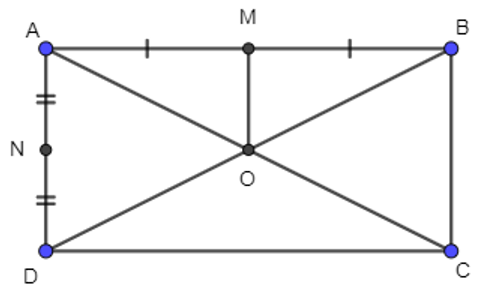
+) Ta có M là trung điểm của AB nên ta có: . Do đó D sai.
+) Ta lại có ABCD là hình chữ nhật nên AB // CD, AB = CD và hai vectơ , cùng hướng nên . Do đó A sai.
+) Xét tam giác ABD, có:
M là trung điểm của AB
O là trung điểm của BD
⇒ MO là đường trung bình của tam giác ABD
⇒ MO = AD
Mà AN = ND = AD nên MO = AN.
Ta thấy và cùng hướng nên . Do đó B đúng.
Hai vectơ và không cùng phương nên không thể bằng nhau. Do đó C sai.
Câu 26:
13/07/2024Phát biểu nào sau đây là sai?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Vectơ là đoạn thẳng có hướng và độ dài của vectơ là khoảng cách giữa điểm đầu và điểm cuối của vectơ đó. Do đó A và B đúng.
Hai vectơ cùng hướng thì cùng phương còn ngược lại hai vectơ cùng phương thì chưa chắc cùng hướng. Do đó C đúng, D sai.
Câu 27:
18/07/2024Cho hình thang MNPQ, MN // PQ, MN = 2PQ. Phát biểu nào dưới đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Câu 28:
21/07/2024Cho tam giác đều ABC nội tiếp đường tròn tâm O bán kính bằng 1. Gọi M là điểm nằm trên đường tròn (O), độ dài vectơ bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Câu 29:
14/07/2024Cho tam giác ABC đều có cạnh bằng a, gọi H là trung điểm của cạnh BC. Độ dài của vectơ 2()bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Câu 30:
18/07/2024 Xem đáp án
Xem đáp án
+) Xét bất phương trình x – y ≥ – 2
Vẽ đường thẳng d1: x – y = – 2 ;
Lấy điểm O(0; 0) ∉ d1 có 0 – 0 = 0 > – 2. Do đó O(0; 0) thuộc vào miền nghiệm của bất phương trình.
Do đó miền nghiệm D1 là nửa mặt phẳng có bờ là đường thẳng d1 chứa điểm O và kể cả đường thẳng d1.
+) Xét bất phương trình x + y ≤ 4
Vẽ đường thẳng d2: x + y = 4;
Lấy điểm O(0; 0) ∉ d2 có 0 + 0 = 0 < 4. Do đó O(0; 0) thuộc vào miền nghiệm của bất phương trình.
Do đó miền nghiệm D2 là nửa mặt phẳng có bờ là đường thẳng d2 chứa điểm O và kể cả đường thẳng d2.
+) Xét bất phương trình x – 5y ≤ – 2
Vẽ đường thẳng d3: x – 5y = – 2;
Lấy điểm O(0; 0) ∉ d3 có 0 – 5.0 = 0 > – 2. Do đó O(0; 0) không thuộc vào miền nghiệm của bất phương trình.
Do đó miền nghiệm D3 là nửa mặt phẳng có bờ là đường thẳng d3 không chứa điểm O và kể cả đường thẳng d3.
Vậy miền nghiệm của hệ bất phương trình là giao của ba miền nghiệm D1, D2 và D3 là miền trong của tam giác ABC có A(1; 3), B(3; 1), C(– 2; 0).

Giá trị nhỏ nhất của biểu thức F(x; y) đạt được trên các đỉnh của tam giác ABC.
Ta có:
Tại điểm A(1; 3) ta có: F(x; y) = – 2.1 + 3 = 1.
Tại điểm B(3; 1) ta có: F(x; y) = – 2.3 + 1 = – 5.
Tại điểm C(– 2; 0) ta có: F(x; y) = – 2.(– 2) + 0 = 4.
Vậy giá trị nhỏ nhất của F(x; y) = – 5.
Bài thi liên quan
-
Đề thi Giữa kì 1 Toán 10 Cánh diều có đáp án - Đề 1
-
28 câu hỏi
-
50 phút
-
Có thể bạn quan tâm
- Đề thi Giữa kì 1 Toán 10 Cánh diều có đáp án (487 lượt thi)
- Đề thi Học kì 1 Toán 10 Cánh diều có đáp án (520 lượt thi)
Các bài thi hot trong chương
- Đề kiểm tra cuối học kì 2 Toán 10 Cánh Diều có đáp án (888 lượt thi)
- Đề kiểm tra giữa học kì 2 Toán 10 Cánh Diều có đáp án (737 lượt thi)

