Đại cương về dao động điều hòa
Đại cương về dao động điều hòa
-
336 lượt thi
-
13 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
23/07/2024Một vật dao động điều hòa với phương trình \[x = Acos\left( {\omega t + \varphi } \right)\]. \(\varphi \) được gọi là:
Xem đáp án
Ta có: \[x = Acos\left( {\omega t + \varphi } \right)\]
+ x: li độ dao động của vật
+ A: Biên độ dao động của vật
+ \(\omega \): Tần số góc của dao động
+ \(\varphi \): Pha ban đầu của dao động
+ \[\omega t + \varphi \]: Pha dao động tại thời điểm t
Đáp án cần chọn là: B
Câu 2:
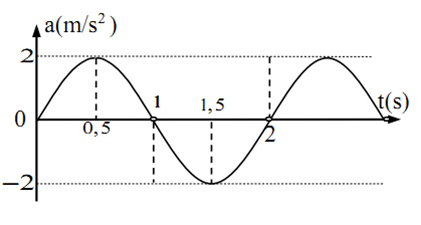
23/07/2024Vật dao động điều hòa hàm cosin có gia tốc biểu diễn như hình. Biên độ và pha ban đầu của vật là:
Xem đáp án
Ta có:
\(\left\{ {\begin{array}{*{20}{c}}{A{\omega ^2} = 2m/{s^2}}\\{T = 2s \to \omega = \pi rad/s}\end{array}} \right. \to A = \frac{2}{{{\pi ^2}}} = 0,2m = 20cm\)
Tại t = 0: a = 0 và đang đi lên =>x = 0 và đi theo chiều âm.
\( \to \left\{ {\begin{array}{*{20}{c}}{x = 0}\\{v < 0}\end{array}} \right. \leftrightarrow \left\{ {\begin{array}{*{20}{c}}{Acos\varphi \; = {\rm{ }}0}\\{sin\varphi >0}\end{array}} \right. \leftrightarrow \left\{ {\begin{array}{*{20}{c}}{cos\varphi \; = {\rm{ }}0}\\{sin\varphi >0}\end{array} \to \varphi = \frac{\pi }{2}} \right.\)
\[ \to A = 20cm,\varphi = \frac{\pi }{2}\]
Đáp án cần chọn là: D
Câu 3:
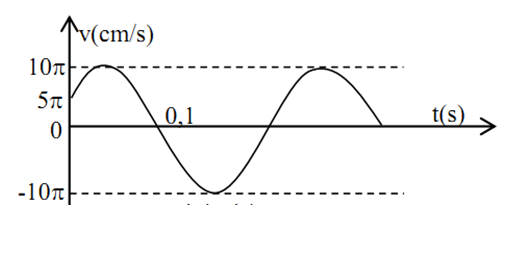
23/07/2024Vật dao động điều hòa có đồ thị vận tốc - thời gian như hình vẽ. Tần số góc và pha ban đầu của li độ của vật là:
Xem đáp án
Ta có:
\(\left\{ {\begin{array}{*{20}{c}}{A\omega = 10\pi cm/s}\\{\frac{{5T}}{{12}} = 0,1s \to T = 0,24s \to \omega = \frac{{25\pi }}{3}rad/s}\end{array}} \right.\)
Tại t = 0:
\(\left\{ {\begin{array}{*{20}{c}}{v = 5\pi }\\{v >0}\end{array}} \right. \leftrightarrow \left\{ {\begin{array}{*{20}{c}}{ - A\omega sin\varphi = 5\pi }\\{sin\varphi < 0}\end{array}} \right. \leftrightarrow \left\{ {\begin{array}{*{20}{c}}{sin\varphi = \frac{{ - 5\pi }}{{10\pi }} = \frac{{ - 1}}{2}}\\{sin\varphi < 0}\end{array}} \right.\)
\( \to \varphi = \left[ {\begin{array}{*{20}{c}}{ - \frac{\pi }{6}}\\{\frac{{7\pi }}{6}}\end{array}} \right.\)
Mặt khác, vận tốc đang tăng =>\[\varphi = \frac{{7\pi }}{6}\]
Đáp án cần chọn là: B
Câu 4:
23/07/2024Vật có đồ thị dao động như hình vẽ. Vận tốc cực đại có giá trị
![Vật có đồ thị dao động như hình vẽ. Vận tốc cực đại có giá trịTa có:\[A = 6cm\]\[2T = 0,4{\rm{s}} \to T = 0,2{\rm{s}} \to \omega {\rm{\; = \;}}\frac{{2\pi }}{T} = 10\pi ra{\rm{d}}/s\]\[ \to (ảnh 1)](https://video.vietjack.com/upload2/images/1649232004/1649232180-image3.png)
Xem đáp án
Ta có:
\[A = 6cm\]
\[2T = 0,4{\rm{s}} \to T = 0,2{\rm{s}} \to \omega {\rm{\; = \;}}\frac{{2\pi }}{T} = 10\pi ra{\rm{d}}/s\]
\[ \to {v_{{\rm{max}}}} = A\omega = 60\pi cm/s\]
Chọn đáp án B
Câu 5:
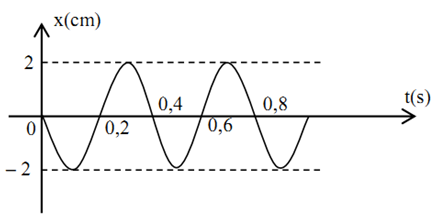
23/07/2024Vật có đồ thị li độ dao động như hình vẽ. Biên độ và chu kì của vật là:
Xem đáp án
Từ đồ thị, ta có:
A = 2cm
T = 0,4s
Đáp án cần chọn là: C
Câu 6:
23/07/2024Tại thời điểm t thì tích của li độ và vận tốc của vật dao động điều hòa âm (x.v < 0), khi đó
Xem đáp án
Ta có: x.v < 0, có thể xảy ra 2 TH
+ x >0,v < 0 : Vật đi từ A =>0: Vật đang chuyển động danh dần theo chiều âm
+ x < 0, v >0: Vật đi từ -A=>0: Vật đang chuyển động nhanh dần theo chiều dương
=>x.v <0: Vật đang chuyển động nhanh dần về vị trí cân bằng
Đáp án cần chọn là: B
Câu 7:
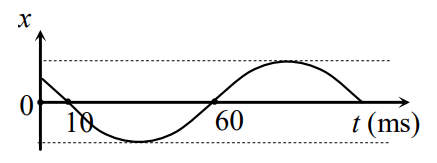
23/07/2024Một vật dao động điều hòa có đồ thị biểu diễn li độ x theo thời gian t như hình bên. Chu kì dao động của vật là
Xem đáp án
Từ đồ thị ta thấy trong khoảng thời gian từ 10 ms đến 60 ms, vật thực hiện được \(\frac{1}{2}\) chu kì:
\[\frac{T}{2} = 60 - 10 \Rightarrow T = 100\,\,\left( {ms} \right) = 0,1\,\,\left( s \right)\]
Đáp án cần chọn là: C
Câu 8:
23/07/2024Một vật dao động điều hoà chu kỳ T. Gọi vmaxvà amaxtuơng ứng là vận tốc cực đại và gia tốc cực đại của vật. Hệ thức liên hệ sai giữa vmaxvà amaxlà:
Xem đáp án
Ta có: \(\left\{ {\begin{array}{*{20}{c}}{{v_{max}} = \omega A}\\{{a_{max}} = {\omega ^2}A}\end{array}} \right. \to \left[ {\begin{array}{*{20}{c}}{\frac{{{a_{max}}}}{{{v_{max}}}} = \frac{{{\omega ^2}A}}{{\omega A}} = \omega = \frac{{2\pi }}{T}}\\{\frac{{{a_{max}}}}{{{v^2}_{max}}} = \frac{{{\omega ^2}A}}{{{{\left( {\omega A} \right)}^2}}} = \frac{1}{A}}\\{\frac{{{a^2}_{max}}}{{{v_{max}}}} = \frac{{{{\left( {{\omega ^2}A} \right)}^2}}}{{\omega A}} = {\omega ^3}A}\end{array}} \right.\)
Đáp án cần chọn là: C
Câu 9:
23/07/2024Trong các phương trình sau phương trình nào không biểu thị cho dao động điều hòa ?
Xem đáp án
B- không biểu thị cho dao động điều hòa vì biên độ dao động không phải là hàm của thời gian
Đáp án cần chọn là: B
Câu 10:
23/07/2024Một vật dao động điều hòa trên quỹ đạo dài 8cm với chu kì T = 2s. Chọn gốc thời gian là lúc vật đi qua vị trí cân bằng theo chiều dương. Phương trình dao động của vật là :
Xem đáp án
Trả lời:
Ta có:\[L = 2A = 8cm = >A = 4cm\]
Tần số góc:\[\omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{2} = \pi ra{\rm{d}}/s\]
Tại t = 0:\(\left\{ {\begin{array}{*{20}{c}}{x = Acos\varphi = 0}\\{v = - A\omega sin\varphi >0}\end{array}} \right. \to \left\{ {\begin{array}{*{20}{c}}{cos\varphi = 0}\\{sin\varphi < 0}\end{array}} \right. \to \varphi = - \frac{\pi }{2}\)
\[ \Rightarrow x = 4cos\left( {\pi t - \frac{\pi }{2}} \right)\]
Đáp án cần chọn là: D
Câu 11:
23/07/2024Một vật dao động điều hoà có đồ thị như hình vẽ.
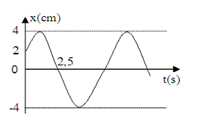
Phương trình dao động của vật là:
Xem đáp án
Từ đồ thị, ta có: A = 4cm
Thời gian vật đi từ t = 0 \[{\rm{\;}}\left( {x = \frac{A}{2}} \right)\] đến t = 2,5s (x = 0) là:\[{\rm{\Delta }}t = 2,5{\rm{s}} = \frac{T}{6} + \frac{T}{4} = \frac{{5T}}{{12}} \to T = 6{\rm{s}} \to \omega = \frac{{2\pi }}{T} = \frac{\pi }{3}ra{\rm{d}}/s\]
Tại t = 0:\(\left\{ {\begin{array}{*{20}{c}}{x = Acos\varphi = 2}\\{v = - A\omega sin\varphi >0}\end{array}} \right. \to \left\{ {\begin{array}{*{20}{c}}{cos\varphi = \frac{2}{4} = \frac{1}{2}}\\{sin\varphi < 0}\end{array}} \right. \to \varphi = - \frac{\pi }{3}\)
\[ \Rightarrow x = 4c{\rm{os}}\left( {\frac{\pi }{3}t - \frac{\pi }{3}} \right)cm\]
Đáp án cần chọn là: A
Câu 12:
23/07/2024Khi nói về một vật dao động điều hòa có biên độ A và chu kì T, với mốc thời gian (t = 0) là lúc vật ở vị trí biên, phát biểu nào sau đây là sai?
Xem đáp án
Ta có: t = 0, x0= A
A - sai vì sau T/8 vật ở vị trí có li độ
\[x = \frac{{A\sqrt 2 }}{2} \to S = A - \frac{{A\sqrt 2 }}{2}\]
B, C, D - đúng
Đáp án cần chọn là: A
Câu 13:
23/07/2024Một vật dao động điều hoà với phương trình \[x = Acos(\omega t + \frac{\pi }{3})cm\] cm. Biết quãng đường vật đi được trong thời gian 1s tính từ thời điểm gốc là 2A và trong \(\frac{2}{3}\)s là 9cm. Giá trị của A và \(\omega \) là:
Xem đáp án
Ta có khoảng thời gian vật đi được quãng đường 2A là \[\frac{T}{2}\]
\[ \to \frac{T}{2} = 1{\rm{s}} \to T = 2{\rm{s}} \to \omega = \frac{{2\pi }}{T} = \pi ({\rm{r}}a{\rm{d}}/{\rm{s}})\]
Tại t = 0
\(\left\{ {\begin{array}{*{20}{c}}{{x_0} = Acos\frac{\pi }{3} = \frac{A}{2}}\\{v = - A\omega sin\frac{\pi }{3} < 0}\end{array}} \right.\)
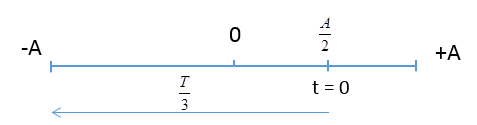
Trong khoảng thời gian \[{\rm{\Delta }}t = \frac{2}{3}s = \frac{T}{3}\] từ thời điểm gốc vật đi được quãng đường S = 9cm
Ta có: \[S = \frac{A}{2} + A = 1,5A = 9cm \to A = 6cm\]
Đáp án cần chọn là: B