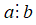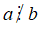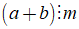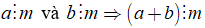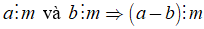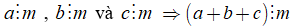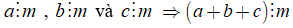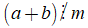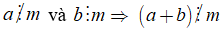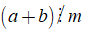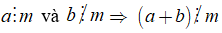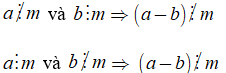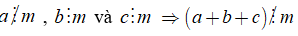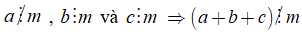Bài tập: Tính chất chia hết của một tổng chọn lọc, có đáp án
-
349 lượt thi
-
18 câu hỏi
-
15 phút
Danh sách câu hỏi
Câu 1:
22/07/2024Nếu a không chia hết cho 2 và b chia hết cho 2 thì tổng a + b
Xem đáp án
Đáp án là B
Theo tính chất 2: Nếu a không chia hết cho 2 và b chia hết cho 2 thì a + b không chia hết cho 2
Câu 2:
22/07/2024Tổng nào sau đây chia hết cho 7
Xem đáp án
Đáp án là A
Theo tính chất 1: Ta có 49 chia hết cho 7 và 70 chia hết cho 7 nên 49 + 70 chia hết cho 7.
Câu 3:
22/07/2024Nếu x ⋮ 2 và y ⋮ 4 thì tổng x + y chia hết cho?
Xem đáp án
Đáp án là A
Ta có: y ⋮ 4 ⇒ y ⋮ 2
x ⋮ 2 và y ⋮ 2 ⇒ (x + y) ⋮ 2
Câu 5:
22/07/2024Chọn câu sai
Xem đáp án
Đáp án là C
Ta có: 18 ⋮ 9; 54 ⋮ 9; 12 không chia hết 9 ⇒ (18 + 54 + 12) không chia hết 9
Đáp án C sai.
Câu 6:
23/07/2024Có tổng M = 75 + 120 + x. Với giá trị nào của x dưới dây thì M ⋮ 3?
Xem đáp án
Đáp án là D
Ta có: 75 ⋮ 3; 120 ⋮ 3. Vậy để M ⋮ 3 thì x ⋮ 3
Trong bốn đáp án ta thấy chỉ có x = 12 thỏa mãn điều kiện
Do đó giá trị cần tìm là x = 12
Câu 7:
22/07/2024Tìm số tự nhiên x để A = 75 + 1003 + x chia hết cho 5
Xem đáp án
Đáp án là C
Ta thấy 75 chia hết cho 5 và 1003 không chia hết cho 5
Nên để A = 75 + 1003 + x chia hết cho 5 thì (1003 + x) chia hết cho 5
Mà 1003 chia cho 5 dư 3 nên để (1003 + x) chia hết cho 5 thì x chia cho 5 dư 2
Câu 8:
11/10/2024Cho A = 12 + 15 + 36 + x, x ∈ ℕ. Tìm điều kiện của x để A không chia hết cho 9.
Xem đáp án
Đáp án cần chọn là: B
* Phương pháp giải:
Sử dụng một trong hai tính chất để tìm điều kiện của x để A không chia hết cho 9
Tính chất 1: Nếu tất cả các số hạng của một tổng (hoặc hiệu) cùng chia hết cho cùng một số thi tổng (hoặc hiệu) chia hết cho số đó.
Tính chất 2: Nếu chỉ có một só hạng của tổng không chia hết cho một số, còn các số hạng khác đều chia hết cho số đó thì tổng (hoặc hiệu) không chia hết cho số đó.
* Lời giải:
Ta có: A = (12 + 15) + 36 + x
Vì 12 + 15 = 27 ⋮ 9; 36 ⋮ 9 ⇒ (12 + 15 + 36) ⋮ 9
Do đó để A không chia hết cho 9 thì x không chia hết cho 9
* Một số lý thuyết liên quan:
1. Nhắc về quan hệ chia hết
Số tự nhiên a chia hết cho số tự nhiên b khác 0 nếu có số tự nhiên k sao cho a = b.k
+ Kí hiệu a chia hết cho b là 
+ Kí hiệu a không chia hết cho b là 
2. Tính chất 1
Nếu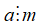 
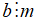
và 
thì 
+ Kí hiệu "⇒" được đọc là suy ra hoặc kéo theo.
+ Ta có thể viết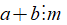 
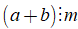
hoặc 
đều được.
Chú ý:
• Tính chất 1 cũng đúng đối với một hiệu
• Tính chất 1 cũng đúng với một tổng nhiều số hạng
Tổng quát: Nếu tất cả các số hạng của một tổng đều chia hết cho cùng một số thì tổng chia hết cho số đó.
3. Tính chất 2.
Nếu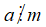 
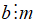
và 
thì 
Nếu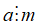 
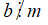
và 
thì 
+ Kí hiệu "⇒" được đọc là suy ra hoặc kéo theo.
+ Ta có thể viết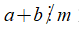 
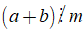
hoặc 
đều được.
Chú ý:
• Tính chất 2 cũng đúng đối với một hiệu
• Tính chất 2 cũng đúng với một tổng nhiều số hạng, trong đó chỉ có một số hạng không chia hết cho m, các số hạng còn lại đều chia hết cho m:
Tổng quát: Nếu chỉ có một số hạng của tổng không chia hết cho một số , còn các số hạng còn lại đều chia hết cho số đó thì tổng đó không chia hết cho số đó.
Xem thêm các bài viết liên quan hay, chi tiết:
TOP 40 câu Trắc nghiệm Quan hệ chia hết. Tính chất chia hết (Cánh diều 2024) có đáp án - Toán 6
Trắc nghiệm Quan hệ chia hết. Tính chất chia hết có đáp án ( Thông hiểu )
Câu 9:
22/07/2024Trong các khẳng định sau, khẳng định nào sai?
Xem đáp án
Đáp án là B
Dựa vào các tính chất chia hết ta thấy đáp án A, C, D đúng
Đáp án B sai. Ví dụ:
Ta có: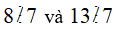 
nhưng 8 + 13 = 21 ⋮ 7
Câu 10:
22/07/2024Khi chia số tự nhiên a cho 12, ta được số dư là 8. Khẳng định nào sau đây đúng?
Xem đáp án
Đáp án là B
Số tự nhiên a chia cho 12 được số dư là 8 nên a = 12k + 8, k ∈ ℕ
Ta có: 12k ⋮ 4; 8 ⋮ 4 ⇒ 12k + 8 ⋮ 4
Câu 11:
22/07/2024Cho với k > 1. Khi đó chia hết cho số nào dưới đây?
Xem đáp án
Đáp án cần chọn là: D
Ta có:
Vậy M19
Câu 12:
22/07/2024Khi chia số a cho 12 ta được số dư là 9. Khi đó:
Xem đáp án
Đáp án cần chọn là: B
Vì a chia cho 12 được số dư là 9 nên a=12k+9(k∈N)
Vì 12k⋮3;9⋮3⇒a=(12k+9)⋮3
Và 12k⋮4;9 không chia hết cho 4 nên a=12k+9 không chia hết cho 4.
Vậy a chia hết cho 3 nhưng không chia hết cho 4.
Câu 13:
23/07/2024Với a,b là các số tự nhiên, nếu 10a + b chia hết cho 13 thì a + 4b chia hết cho số nào dưới đây?
Xem đáp án
Đáp án cần chọn là: D
Xét 10.(a+4.b)=10.a+40.b=(10.a+b)+39.b .
Vì (10.a+b)⋮13 và 39b⋮13 nên 10.(a+4.b)⋮13 .
Do 10 không chia hết cho 13 nên suy ra (a+4.b)⋮13 .
Vậy nếu 10a+b chia hết cho 13 thì a+4b chia hết cho 13
Câu 14:
23/07/2024Với a,b là các số tự nhiên, nếu 11a + 2b chia hết cho 8 thì a + 6b chia hết cho số nào dưới đây?
Xem đáp án
Đáp án cần chọn là: A
Xét 11.(a+6.b)=11.a+66.b=(11.a+2b)+64.b
Vì (11.a+2b)⋮8 và 64b⋮8 nên 11.(a+6.b)⋮8.
Do 11 không chia hết cho 8 nên suy ra (a+6.b)⋮8.
Vậy nếu 11a+2b chia hết cho 8 thì a+6b chia hết cho 8.
Câu 15:
23/07/2024Có bao nhiêu số tự nhiên n để (n + 7) chia hết cho (n + 2)?
Xem đáp án
Đáp án cần chọn là: C
Vì (n+2)⋮(n+2) nên theo tính chất 1 để (n+7)⋮(n+2) thì [(n+7)−(n+2)]⋮(n+2) hay 5⋮(n+2) .
Suy ra (n+2)∈{1;5} .
Vì n+2≥2 nên n+2=5⇒n=5–2=3.
Vậy n=3.
Vậy có một số tự nhiên n thỏa mãn yêu cầu.
Câu 16:
22/07/2024Có bao nhiêu số tự nhiên n để (n + 9) chia hết cho (n + 5) ?
Xem đáp án
Đáp án cần chọn là: D
Vì (n+5)⋮(n+5) nên theo tính chất 1 để (n+9)⋮(n+5) thì [(n+9)−(n+5)]⋮(n+5) hay 4⋮(n+5).
Suy ra (n+5)∈{1;2;4}.
Vì n+5≥5 nên không có giá trị của n thỏa mãn.
Câu 17:
22/07/2024Chọn câu sai.
Xem đáp án
Đáp án cần chọn là: D
+) Gọi ba số tự nhiên liên tiếp là n; n+1; n+2 (n∈N) thì tổng ba số tự nhiên liên tiếp là n+n+1+n+2=3n+3. Vì 3⋮3 nên (3n+3)⋮3 suy ra A đúng.
+) Gọi bốn số tự nhiên liên tiếp là n;n+1;n+2;n+3 (n∈N) thì tổng bốn số tự nhiên liên tiếp là n+n+1+n+2+n+4=4n+7. Vì 4n⋮4;7⋮̸4 nên (4n+7)⋮̸4 suy ra B đúng, D sai.
+) Gọi năm số tự nhiên chẵn liên tiếp là 2n; 2n+2; 2n+4; 2n+6; 2n+8 (n∈N) thì tổng năm số tự nhiên chẵn liên tiếp là 2n+2n+2+2n+4+2n+6+2n+8=10n+20. Vì 10n⋮10;20⋮10 nên (10n+20)⋮10 suy ra C đúng.
