Bài tập Hình học Khối đa diện cơ bản, nâng cao có lời giải chi tiết
Bài tập Hình học Khối đa diện cơ bản, nâng cao có lời giải chi tiết (P1) (Đề 3)
-
912 lượt thi
-
30 câu hỏi
-
40 phút
Danh sách câu hỏi
Câu 1:
13/07/2024Cho khối chóp S.ABC có SA=a, SB=2a, SC=3a. Thể tích lớn nhất của khối chóp là
 Xem đáp án
Xem đáp án
Chọn D
Gọi H là hình chiếu của S lên mặt phẳng (ABC).
Dấu “=” xảy ra khi SA,SB,SC vuông góc với nhau từng đôi một.
Câu 2:
21/07/2024Cho hình trụ thiết diện qua trục hoành là hình vuông ABCD cạnh cm với AB là đường kính của đường tròn đáy tâm O. Gọi M là điểm thuộc cung AB sao cho . Tính thể tích của khối tứ diện ACDM.
 Xem đáp án
Xem đáp án
Chọn B
Ta có:
Câu 3:
13/07/2024Cho hình lăng trụ đứng tam giác ABC.A'B'C' tam giác ABC có AB=a,AC = , góc , A'C=. Tính thể tích khối lăng trụ ABC.A'B'C' là
 Xem đáp án
Xem đáp án
Chọn C
Câu 4:
23/07/2024Cho hình chữ nhật ABCD và nửa đường tròn đường kính AB như hình vẽ. Gọi M, N lần lượt là trung điểm của AB, CD. Biết AB = 4,AD = 7. Tính thể tích V của vật thể tròn xoay khi quay mô hình trên quanh trục MN.
 Xem đáp án
Xem đáp án
Chọn D
Khi quay mô hình đã cho quanh trục MN ta được một khối tròn xoay gồm:
- hình trụ có chiều cao là AD, đáy là hình tròn(M,MA), có thể tích ;
- nửa hình cầu tâm M bán kính MA, có thể tích
Câu 5:
13/07/2024Cho khối đa diện đều n mặt có thể tích là V và diện tích mỗi mặt của nó là S. Khi đó tổng khoảng cách từ một điểm bất kì bên trong khối đa diện đó đến các mặt của nó bằng
 Xem đáp án
Xem đáp án
Đáp án D
Gọi O là một điểm bất kì bên trong khối đa diện.
Chia khối đa diện đều n mặt đã cho thành n khối chóp có đỉnh là O và các mặt đáy là các mặt của khối đa diện. Chiều cao hạ từ O đến n mặt tương ứng là
Khi đó
Câu 6:
13/07/2024Cho hình chóp S.ABC có các cạnh SA=SB=SC=BA=BC=a. Tìm thể tích lớn nhất của hình chóp S.ABC.
 Xem đáp án
Xem đáp án
Chọn C
Câu 7:
13/07/2024Cho hình hộp chữ nhật ABCD.A’B’C’D’ có đáy là hình vuông cạnh a và cạnh bên bằng 3a. Diện tích xung quanh Sxq của hình nón có đỉnh là tâm O của hình vuông A’B’C’D’ có đáy là hình tròn nội tiếp hình vuông ABCD là
 Xem đáp án
Xem đáp án
Chọn C
Câu 8:
23/07/2024Cho lăng trụ ABCA’B’C’, đáy là tam giác đều là cạnh bằng a, tứ giác ABB’A’ là hình thoi, , Tính thể tích lăng trụ ABCA’B’C’.
 Xem đáp án
Xem đáp án
Chọn A
Dễ dàng tính được các cạnh của tứ diện CA’B’C’:
Câu 9:
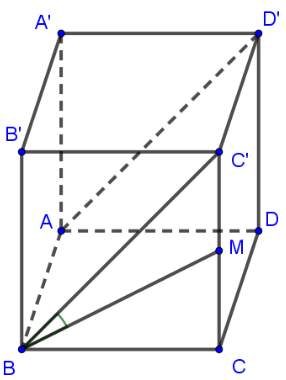
13/07/2024Cho ABCD.A’B’C’D’ là hình lập phương cạnh 2a. Tính thể tích khối tứ diện ACD’B’ là
 Xem đáp án
Xem đáp án
Chọn B
Nhận thấy chóp ACD’B’ có tất cả các cạnh bằng nhau và bằng
Gọi M là trung điểm của AC, G là trọng tâm của tam giác AB’C’. Chóp ACD’B’ nhận D’G là đường cao.
Xét tam giác AB’C có
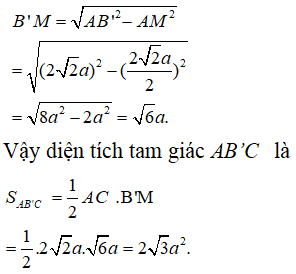
Xét tam giác vuông D’GB’ ta có
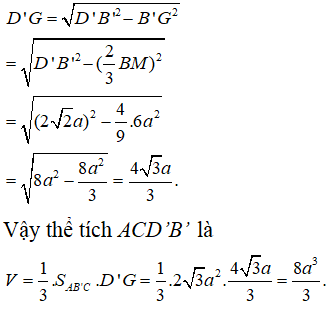
Câu 10:
18/07/2024Cho hình lăng trụ tam giác đều ABC.A'B'C' có góc giữa hai mặt phẳng (A'BC) và (ABC) bằng , cạnh AB = 2. Thể tích V của khối lăng trụ ABC.A'B'C' là
 Xem đáp án
Xem đáp án
Chọn C
Câu 11:
13/07/2024Hình hộp chữ nhật có độ dài ba cạnh xuất phát từ một đỉnh lần lượt là 3, 4, 5. Thể tích của hình hộp đó là
 Xem đáp án
Xem đáp án
Chọn C
Thể tích hình hộp đó là V = 3.4.5 = 60
Câu 12:
20/07/2024Cho hình lập phương ABCD.A'B'C'D' có các cạnh bằng 1. M là trung điểm CC'. Tính góc giữa hai đường thẳng AD' và BM
 Xem đáp án
Xem đáp án
Chọn B
Câu 13:
21/07/2024Khối lăng trụ ABC.A'B'C' có đáy là tam giác đều, a là độ dài cạnh đáy. Góc giữa cạnh bên và đáy là . Hình chiếu vuông góc của A' trên mặt (ABC) trùng với trung điểm của BC. Diện tích xung quanh của lăng trụ đã cho là
 Xem đáp án
Xem đáp án
Chọn C

Câu 14:
20/07/2024Cho hình chóp tam giác S.ABC có đáy là tam giác đều cạnh a, cạnh bên SA vuông góc với đáy và . Thể tích V của khối chóp S.ABC là
 Xem đáp án
Xem đáp án
Chọn D
Câu 15:
18/07/2024Cho hình thang vuông ABCD có , AB=AD=2cm, CD=2AB. Tính thể tích khối tròn xoay tạo thành khi quay hình thang quanh trục là cạnh AB.
 Xem đáp án
Xem đáp án
Chọn B
Ta có thể tích khối tròn xoay tạo thành bằng hiệu
thể tích hình trụ bán kính đáy AD, chiều cao
CD trừ cho thể tích nón đỉnh B, bán kính đáy
BM chiều cao CM.
Ta có:
Câu 16:
20/07/2024Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = a, AA - 2a. Biết thể tích hình cầu ngoại tiếp tứ diện ABCD' là .
Tính thể tích V của hình chữ nhật
 Xem đáp án
Xem đáp án
Chọn C
Từ (1), (2) dễ dàng suy ra trung điểm I của
BD' là tâm mặt cầu ngoại tiếp tứ diện ABCD'
Ta có
Câu 17:
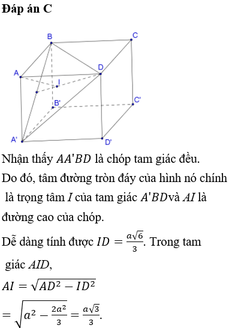
19/07/2024Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Khối nón đỉnh A, đáy là đường tròn đi qua ba điểm A'BD có thể tích bằng
 Xem đáp án
Xem đáp án
Chọn C
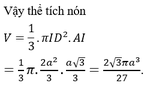
Câu 18:
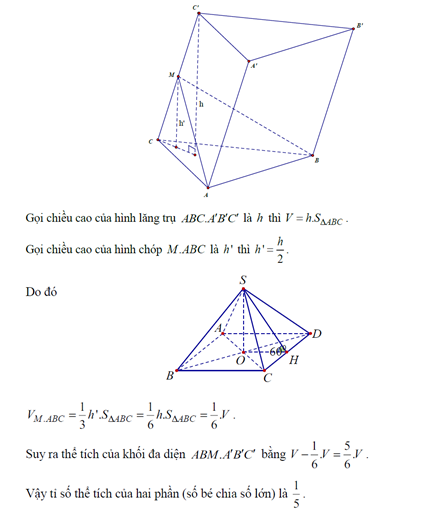
23/07/2024Cho khối lăng trụ tam giác ABC.A'B'C' có thể tích V. Gọi M là trung điểm của CC'. Mặt phẳng (MAB) chia khối trụ thành hai phần. Tính tỷ số thể tích hai phần đó (số bé chia số lớn)
 Xem đáp án
Xem đáp án
Chọn C
Câu 19:
20/07/2024Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a , BC = , SA = a và SA vuông góc với đáy ABCD. Tính sin với là góc tạo bởi giữa đường thẳng BD và mặt phẳng (SBC)
 Xem đáp án
Xem đáp án
Chọn A
.png)
Ta có ABCD là hình chữ nhật nên BD = 2a,
ta có AD // (SBC) nên suy ra d[D,(SBC)] = d[A,(SBC)] = AH với AH ⊥ SB
Tam giác SAB vuông cân tại A nên H là trung điểm của SB suy ra
Vậy
Câu 20:
21/07/2024Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy và SB = 2a. Góc giữa đường thẳng SB và mặt phẳng đáy bằng
 Xem đáp án
Xem đáp án
Chọn A
.png)
Ta có AB là hình chiếu của SB trên (ABCD).
Góc giữa đường thẳng SB và mặt phẳng đáy bằng góc giữa SB và AB.
Tam giác SAB vuông tại A,
Câu 21:
27/11/2024Cho hình chóp S.ABC có đáy là tam giác vuông đỉnh B, AB = a, SA vuông góc với mặt phẳng đáy và SA = 2a . Khoảng cách từ A đến mặt phẳng (SBC) bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là A
Lời giải
.png)
Trong tam giác SAB dựng AH vuông góc SB thì
Xét tam giác SAB vuông tại A:
*Phương pháp giải:
1.Xác định khoảng cách cần tìm là AH
2.Dựa vào
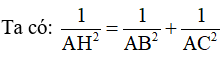
*Lý thuyết:
Định lí 2. Trong một tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng tích hai hình chiếu của hai cạnh góc vuông trên cạnh huyền.
Ví dụ 2. Tam giác ABC vuông tại A, đường cao AH.
Khi đó, BH và CH lần lượt là hình chiếu của AB và AC trên BC.
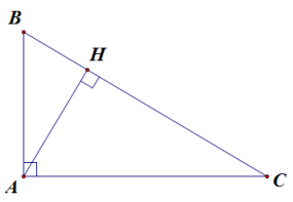
Ta có: AH2 = BH . HC.
Định lí 3. Trong một tam giác vuông, tích hai cạnh góc vuông bằng tích của cạnh huyền và đường cao tương ứng.
Ví dụ 3. Tam giác ABC vuông tại A, đường cao AH.
Khi đó, BH và CH lần lượt là hình chiếu của AB và AC trên BC.
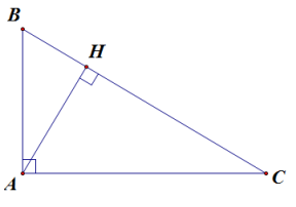
Ta có: AB . AC = BC . AH.
Định lí 4. Trong một tam giác vuông, nghịch đảo của bình phương đường cao ứng với cạnh huyền bằng tổng các nghịch đảo của bình phương hai cạnh góc vuông.
Ví dụ 4. Tam giác ABC vuông tại A, đường cao AH.
Khi đó, BH và CH lần lượt là hình chiếu của AB và AC trên BC.
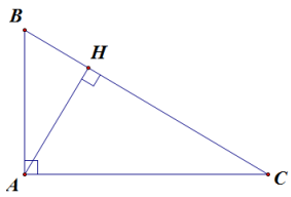
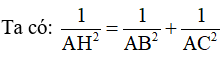
Xem thêm
Lý thuyết Một số hệ thức về cạnh và đường cao trong tam giác vuông (mới 2024 + Bài Tập) – Toán 9
Câu 22:
01/01/2025Cho khối chóp tứ giác đều có tất cả các cạnh bằng 2a. Thể tích của khối chóp đã cho bằng
 Xem đáp án
Xem đáp án
Đáp án đúng: A
*Lời giải:
Cách 2:
Thể tích khối chóp tứ giác đều cạnh a là
*Phương pháp giải
- Áp dụng công thức tính thể tích khối chóp tứ giác đều để tính toán: mặt đáy của khối chóp tứ giác đều là hình vuông, các cạnh từ đỉnh chóp xuống 4 góc sẽ bằng nhau
*Lý thuyết về khối chóp tứ giác đều
a) Hình chóp
- Đáy là một đa giác, các mặt bên là những tam giác có chung một đỉnh.
– Đường thẳng đi qua đỉnh và vuông góc với mặt phẳng đáy gọi là đường cao.
b) Hình chóp đều
Hình chóp đều là hình chóp có đáy là một đa giác đều, các mặt bên là những tam giác cân bằng nhau có chung đỉnh.
+ Chân đường cao của hình chóp đều trùng với tâm của đường tròn đi qua các đỉnh của mặt đáy.
+ Đường cao vẽ từ đỉnh của mỗi mặt bên của hình chóp đều được gọi là trung đoạn của hình chóp đó.
a) Diện tích xung quanh của hình chop đều
Diện tích xung quanh của hình chóp đều bằng tích của nửa chu vi đáy với trung đoạn:
Sxq = p.d (p: nửa chu vi đáy, d: trung đoạn)
b) Diện tích toàn phần của hình chóp
Diện tích toàn phần của hình chóp bằng tổng của diện tích xung quanh và diện tích đáy:
Stp = Sxq + S (S: diện tích đáy)
c) Thể tích của hình chóp bằng một phần ba của diện tích đáy nhân với chiều cao:
V = 1/3S.h (S: diện tích đáy, h: chiều cao)
Xem thêm các bài viết liên quan hay, chi tiết:
Câu 23:
16/07/2024Cho khối cầu (S) ngoại tiếp tứ diện OABC có OA = OB = OC = a và OA, OB, OC đôi một vuông góc. Thể tích của (S) bằng
 Xem đáp án
Xem đáp án
Chọn A
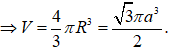
Câu 24:
18/07/2024Cho khối lăng trụ tam giác đều có tất cả các cạnh bằng 2a. Thể tích của khối lăng trụ đã cho bằng
 Xem đáp án
Xem đáp án
Chọn D
Câu 25:
13/07/2024Cho lăng trụ ABC.A’B’C’ có khoảng cách từ điểm A đến mặt phẳng (A’BC) bằng 6a. Khoảng cách từ trung điểm M cạnh B’C’ đến mặt phẳng (A’BC) bằng
 Xem đáp án
Xem đáp án
Chọn C
Câu 26:
22/07/2024Cho khối chóp S.ABCD có đáy là hình bình hành, thể tích bằng 1. Gọi M là trung điểm cạnh SA; các điểm E,F lần lượt là điểm đối xứng của A qua B và D. Mặt phẳng (MEF) cắt các cạnh SB,SD lần lượt tại các điểm N,P. Thể tích của khối đa diện ABCDMNP bằng
 Xem đáp án
Xem đáp án
Chọn A
Cách 2: Dùng công thức tính nhanh tỷ số thể tích
Có
Vì Vậy
Câu 27:
22/07/2024Thể tích khối chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh 2a, tâm O, SO = 3a (tham khảo hình vẽ bên) bằng
 Xem đáp án
Xem đáp án
Chọn B
Câu 28:
21/07/2024Cho khối chóp S.ABCD có đáy là hình thang với hai đáy là AB và CD, AB = 2CD. Gọi E là một điểm trên cạnh SC. Mặt phẳng (ABE) chia khối chóp S.ABCD thành hai khối đa diện có thể tích bằng nhau. Tính tỉ số
 Xem đáp án
Xem đáp án
Chọn A
Vì
Chia khối chóp S.ABEF thành hai khối chóp tam giác S.AEF, S.ABE có
Câu 29:
21/07/2024Cho khối hộp đứng có đáy là một hình thoi có độ dài đường chéo nhỏ bằng 10 và góc nhọn bằng
 Xem đáp án
Xem đáp án
Chọn A
Giả sử độ dài cạnh đáy bằng a, thì độ dài của hai đường chéo đáy tính theo định lí hàm số côsin bằng
Câu 30:
20/07/2024Cho hình lăng trụ đều có độ dài cạnh đáy bằng a. Chiều cao của hình lăng trụ bằng h, diện tích một mặt đáy bằng S. Tổng khoảng cách từ một điểm trong của hình lăng trụ đến tất cả các mặt của hình lăng trụ bằng
 Xem đáp án
Xem đáp án
Chọn A
Xét hình lăng trụ đều (H) đã cho có đáy là đa giác đều n đỉnh. Xét điểm trong I của hình lăng trụ đều (H) đã cho. Khi đó nối I với các đỉnh của (H) ta được n+2 khối chóp có đỉnh là I, trong đó có hai khối chóp có đỉnh là I và mặt đáy là mặt đáy của (H); và n khối chóp có đỉnh I và mặt đáy là mặt bên của (H). Diện tích mỗi mặt
đáy của (H) bằng S; diện tích mỗi mặt bên của (H) bằng ah. Gọi h1, h2, .., hn, hn+1, hn+2 lần lượt là khoảng cách từ I đến các mặt bên của (H) và các mặt đáy của (H). Vậy theo công thức tính thể tích của khối lăng trụ và khối chóp ta có:
Chú ý tổng khoảng cách từ I đến hai mặt đáy của (H) là

.PNG)