30 câu hỏi trắc nghiệm thuộc Bài tập Hàm số mũ, logarit ôn thi Đại học có lời giải (P1) (Đề 5)

Câu 1:

19/07/2024

Giải phương trình $\log_{2017} (13 x + 3) = \log_{2017} 16$

Xem đáp án

Câu 2:

20/07/2024

Tìm tập nghiệm S của phương trình $\log_{6} [x (5 - x)] = 1$

Xem đáp án

Câu 3:

13/07/2024

Tìm tất cả các giá trị thực của tham số a để biểu thức $B = \log_{3} (2 - a)$ có nghĩa

Xem đáp án

Câu 4:

13/07/2024

Đặt $a = \log_{12} 6, b = \log_{12} 7$ . Hãy biểu diễn $\log_{2} 7$ theo a và b.

Xem đáp án

Câu 5:

19/07/2024

Biết phương trình $2 \log_{2} x + 3 \log_{x} 2 = 7$ có hai nghiệm thực $x_{1} < x_{2}$ . Tính giá trị của biểu thức $T = {(x_{1})}^{x_{2}}$

A. T=64

B. T=32

C. T=8

D. T=16

Xem đáp án

Câu 6:

17/07/2024

Cho $0 < a < 1$ . Chọn khẳng định đúng trong các khẳng định sau :

Xem đáp án

Câu 7:

23/07/2024

Cho phương trình: ${(7 + 4 \sqrt{3})}^{x^{2} + x - 1} = {(2 + \sqrt{3})}^{x - 2}$ . Chọn khẳng định đúng trong các khẳng định sau:

A. Phương trình có hai nghiệm không dương.

B. Phương trình có hai nghiệm dương phân biệt.

C. Phương trình có hai nghiệm trái dấu.

D. Phương trình có hai nghiệm âm phân biệt.

Xem đáp án

Câu 8:

13/07/2024

Với $0 < a \neq 1,$ biểu thức nào sau đây có giá trị dương?

Xem đáp án

Câu 9:

21/07/2024

Cho x, y là các số thực dương thỏa mãn điều kiện $5^{x + 2 y} + \frac{3}{3^{x y}} + x + 1 = \frac{5^{x y}}{5} + 3^{- x - 2 y} + y (x - 2)$ .

Tính giá trị nhỏ nhất của biểu thức $T = x + y$ .

Xem đáp án

Câu 10:

13/07/2024

Với a, b, c là các số thực dương, a và c khác 1 và $a \neq 0$ . Mệnh đề nào dưới đây sai?

A: $\log_{a} b \log_{b} a = \log_{a} b$

Xem đáp án

Câu 11:

21/07/2024

Cho $\log_{2} 3 = a$ . Tính $T = \log_{36} 24$ theo a

Xem đáp án

Câu 12:

13/07/2024

Giá trị nhỏ nhất, giá trị lớn nhất của hàm số $y = x - \ln x$ trên đoạn $[\frac{1}{2}; e]$ lần lượt là

Xem đáp án

Câu 13:

13/07/2024

Tìm tập nghiệm S của bất phương trình $\log_{\frac{6}{π}} (x + 1) < \log_{\frac{6}{π}} (3 x - 1) .$

Xem đáp án

$B P T \Leftrightarrow \{\begin{cases} x + 1 > 0 \\ 3 x - 1 > 0 \\ x + 1 > 3 x - 1 \end{cases} \Leftrightarrow \{\begin{cases} x > \frac{1}{3} \\ x > 1 \end{cases} \Rightarrow S = (1; + \infty)$

Câu 14:

13/07/2024

Tìm số nghiệm nguyên của phương trình $\sqrt{25 - x^{2}} \log_{2} (x^{2} - 4 x + 5) < 0$

A. 6

B. 5

C. 4

D. 3

Xem đáp án

Câu 15:

20/07/2024

Số nghiệm của phương trình $\log_{3} (x^{2} + 4 x) + \log_{\frac{1}{3}} (2 x + 3) = 0$ là

A. 2

B. 0

C. 1

D. 3

Xem đáp án

Câu 16:

22/07/2024

Cho $0 < a \neq 1$ và $x > 0, y > 0$ . Chọn mệnh đề đúng trong các mệnh đề sau

Xem đáp án

Đáp án B

Theo quy tắc tính lôgarit ta có: $\log_{a} (b c) = \log_{a} b + \log_{a} c$ nên suy ra các đáp án A,C và D sai

Câu 17:

14/07/2024

Cho $a \log_{2} 3 + b \log_{6} 2 + c \log_{6} 3 = 5$ với a, b, c là các số tự nhiên. Khẳng định nào đúng trong các khẳng định sau đây

Xem đáp án

Câu 18:

13/07/2024

Cho $\log_{2} 5 = a$ . Tính $\log_{2} 200$ theo a.

A. 2+2a

B. 4+2a

C. 1+2a

D. 3+2a

Xem đáp án

Câu 19:

13/07/2024

Rút gọn biểu thức $A = a^{4 \log_{a^{2}} 3}$ với $0 < a \neq 1$ ta được kết quả là

A. 9

B. $3^{4}$

C. $3^{8}$

D. 6

Xem đáp án

Câu 20:

19/07/2024

Cho $x = 2017!$ . Gía trị biểu thức $A = \frac{1}{\log_{2^{2}} x} + \frac{1}{\log_{3^{2}} x} + . . . + \frac{1}{\log_{2017^{2}} x}$ bằng

A. $\frac{1}{2}$

B. 2

C. 4

D. 1

Xem đáp án

Câu 21:

13/07/2024

Nếu ${(7 + 4 \sqrt{3})}^{a - 1} < 7 - 4 \sqrt{3}$ thì

A. a<1

B. a>1

C. a>0

D. a<0

Xem đáp án

Câu 22:

21/07/2024

Tìm tất cả các giá trị thực của x thỏa mãn đẳng thức $\log_{3} x = 3 \log_{3} 2 + \log_{9} 25 - \log_{\sqrt{3}} 3$

A. $\frac{40}{9}$

B. $\frac{25}{9}$

C. $\frac{28}{3}$

D. $\frac{20}{3}$

Xem đáp án

Câu 23:

22/07/2024

Cho $0 < a \neq 1$ và $b \in ℝ$ . Chọn mệnh đề sai trong các mệnh đề sau

Xem đáp án

Câu 24:

17/07/2024

Tập nghiệm của phương trình $9^{x} - 4 . 3^{x} = 0$

A. {0;1}

B. {1;3}

C. {0;-1}

D. {1;-3}

Xem đáp án

Câu 25:

14/07/2024

Trong các biểu thức sau, biểu thức nào không có nghĩa

A. ${(- 4)}^{\frac{- 1}{3}}$

B. ${(\frac{- 3}{4})}^{0}$

C. ${(- 3)}^{- 4}$

D. $1^{- \sqrt{2}}$

Xem đáp án

Câu 26:

13/07/2024

Cho $\log_{6} 45 = a + \frac{\log_{2} 5 + b}{\log_{2} 3 + c}, a, b, c \in ℤ$ . Tính tổng a+b+c

A. 1

B. 0

C. 2

D. -4

Xem đáp án

Câu 27:

23/07/2024

Tính tổng tất cả các nghiệm của phương trình sau $3^{2 x + 8} - 4 . 3^{x + 5} + 27 = 0$

A. -5

B. 5

C. $\frac{4}{27}$

D. $\frac{- 4}{27}$

Xem đáp án

Câu 28:

16/10/2024

Bất phương trình $\log_{4} (x + 7) > \log_{2} (x + 1)$ có bao nhiêu nghiệm nguyên?

A. 1

B. 2

C. 4

D. 3

Xem đáp án

Đáp án đúng: B

*Phương pháp giải

- Trước tiên cần tìm điều kiện để biểu thức trong log xác định trước

- Giaỉ bất phương trình hàm log, ta đứa về cùng cơ số dưới log rồi cho biểu thức log bằng nhau và giải tìm ra nghiệm của x trong khoảng nào

*Lời giải

* Lý thuyết cần nắm và các dạng bài về bất phương trình logarit:

Phương trình và bất phương trình lôgarit cơ bản: cho

a,b>0,a≠1

Bất phương trình lôgarit cơ bản có dạng:

$\log_{a} f (x) > b; \log_{a} f (x) \geq b; \log_{a} f (x) < b; \log_{a} f (x) \leq b$

$\log_{a} f (x) > b; \log_{a} f (x) \geq b; \log_{a} f (x) < b; \log_{a} f (x) \leq b$ $\log_{a} f (x) > b; \log_{a} f (x) \geq b; \log_{a} f (x) < b; \log_{a} f (x) \leq b$ + Đưa về cùng cơ số

Nếu $a > 1$ thì $\log_{a} f (x) > \log_{a} g (x)$

$\Leftrightarrow \{\begin{cases} g (x) > 0 \\ f (x) > g (x) \end{cases}$

Nếu $0 < a < 1$ thì $\log_{a} f (x) > \log_{a} g (x)$

$\Leftrightarrow \{\begin{cases} f (x) > 0 \\ f (x) < g (x) \end{cases}$

+ Đặt ẩn phụ

+ Mũ hóa

+ Phương pháp hàm số và đánh giá

CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI

Dạng 1. Bất phương trình logarit cơ bản

Phương pháp giải

Ta có BPT

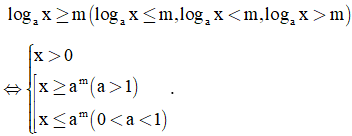
Dạng 2. Phương pháp đưa về cùng cơ số

Phương pháp giải

Xét bất phương trình $\log_{a} f (x) > \log_{a} g (x)$ $(a > 0, a \neq 1)$

Nếu $a > 1$ thì $\log_{a} f (x) > \log_{a} g (x)$ $\Leftrightarrow f (x) > g (x)$ (cùng chiều khi a > 1)

Nếu $0 < a < 1$ thì $\log_{a} f (x) > \log_{a} g (x)$ $\Leftrightarrow f (x) < g (x)$ (ngược chiều khi $0 < a < 1$ )

Nếu a chứa ẩn thì $\log_{a} f (x) > \log_{a} g (x)$ $\Leftrightarrow \{\begin{cases} f (x) > 0; g (x) > 0 \\ (a - 1) [f (x) - g (x)] > 0 \end{cases}$ (hoặc chia 2 trường hợp của cơ số)