Bất phương trình ${\log }_4(x+7)>{\log }_2(x+1)$ có bao nhiêu nghiệm nguyên?

Đáp án đúng: B

*Phương pháp giải

- Trước tiên cần tìm điều kiện để biểu thức trong log xác định trước

- Giaỉ bất phương trình hàm log, ta đứa về cùng cơ số dưới log rồi cho biểu thức log bằng nhau và giải tìm ra nghiệm của x trong khoảng nào

*Lời giải

* Lý thuyết cần nắm và các dạng bài về bất phương trình logarit:

Phương trình và bất phương trình lôgarit cơ bản: cho 

a,b>0,a≠1

Bất phương trình lôgarit cơ bản có dạng:

${\log }_{a}f\left(x\right)>b;{\log }_{a}f\left(x\right)\ge b;\text{log}{}_{a}f\left(x\right)<b;{\log }_{a}f\left(x\right)\le b$

$\mathrm{Phương\; pháp\; giải\; phương\; trình\; và\; bất\; phương\; trình\; lôgarit}$

$$\begin{gathered} {\mathrm{<span><span\; style="box-sizing:\; border-box;\; font-weight:\; bolder;"><span\; style="box-sizing:\; border-box;\; background:\; \#cedde5;\; "\; data-toc-lv="2">Phương\; pháp\; giải\; phương\; trình\; và\; bất\; phương\; trình\; lôgarit</span></span></span>log}}_{a}f\left(x\right)>b;{\log }_{a}f\left(x\right)\ge b; \\ {\log }_{a}f\left(x\right)<b;{\log }_{a}f\left(x\right) \end{gathered}$$+ Đưa về cùng cơ số

Nếu $a>1$ thì ${\log }_{a}f\left(x\right)>{\log }_{a}g\left(x\right)$

$\iff \{\begin{array}{c}g\left(x\right)>0\\ f\left(x\right)>g\left(x\right)\end{array}$

Nếu $0<a<1$ thì ${\log }_{a}f\left(x\right)>{\log }_{a}g\left(x\right)$

$\iff \{\begin{array}{c}f\left(x\right)>0\\ f\left(x\right)<g\left(x\right)\end{array}$

+ Đặt ẩn phụ

+ Mũ hóa

+ Phương pháp hàm số và đánh giá

CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI

Dạng 1. Bất phương trình logarit cơ bản

Phương pháp giải

Ta có BPT

 

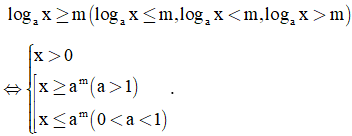
Dạng 2. Phương pháp đưa về cùng cơ số

Phương pháp giải

Xét bất phương trình ${\log }_{a}f\left(x\right)>{\log }_{a}g\left(x\right)$ $(a>0,a\ne 1)$

Nếu $a>1$ thì ${\log }_{a}f\left(x\right)>{\log }_{a}g\left(x\right)$$\iff f\left(x\right)>g\left(x\right)$ (cùng chiều khi a > 1)

Nếu $0<a<1$ thì ${\log }_{a}f\left(x\right)>{\log }_{a}g\left(x\right)$$\iff f\left(x\right)<g\left(x\right)$ (ngược chiều khi $0<a<1$)

Nếu a chứa ẩn thì ${\log }_{a}f\left(x\right)>{\log }_{a}g\left(x\right)$$\iff \{\begin{array}{c}f\left(x\right)>0;g\left(x\right)>0\\ (a-1)\left[f\left(x\right)-g\left(x\right)\right]>0\end{array}$(hoặc chia 2 trường hợp của cơ số)

Xem thêm các bài viết liên quan hay chi tiết:

Lý thuyết và bài toán về hàm số lũy thừa, hàm số mũ, hàm số logarit và cách giải ( có đáp án ) – Toán 12 

Lý thuyết bất phương trình logarit và cách giải các dạng bài tập 

Bài tập Hàm số mũ, logarit ôn thi Đại học có lời giải