Bài tập Hàm số mũ, logarit cơ bản, nâng cao có lời giải
Bài tập Hàm số mũ, logarit cơ bản, nâng cao có lời giải (P1) (Đề 2)
-
1421 lượt thi
-
30 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 19:
02/11/2024Tập nghiệm của bất phương trình là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
*Lời giải
*Phương pháp giải
Với ,
*Mở rộng " Một số dạng toán về phương trình mũ"
Dạng 1. Phương trình mũ cơ bản
ax = b (a > 0, a ≠ 1) . Để giải pt trên, ta sử dụng định nghĩa logarit.
* Với b > 0, ta có ax = b ⇔ x = logab
* Với b ≤ 0, phương trình vô nghiệm.
Dạng 2. Phương pháp đưa về cùng cơ số
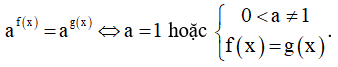
Dạng 3. Phương pháp đăt ẩn phụ
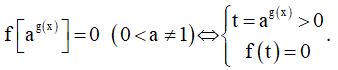
Dạng 4. Phương pháp logarit hóa
+ Phương trình 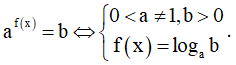
+ Phương trình
af(x) = bg(x) ⇔ logaaf(x) = logabg(x) ⇔ f(x) = g(x).logab
hoặc logbaf(x) = logbbg(x) ⇔ f(x).logba= g(x)
Dạng 5. Phương pháp đồ thị, hàm số, đánh giá
+ Giải bằng phương pháp đồ thị:
Giải phương trình:
ax = f(x) (0 < a ≠ 1) (∗) .
Xem phương trình (∗) là phương trình hoành độ giao điểm của hai đồ thị y = ax (0 < a ≠ 1) và y = f(x). Khi đó ta thực hiện hai bước:
Bước1. Vẽ đồ thị các hàm số
y = ax (0 < a ≠ 1) và y = f(x)
Bước 2. Kết luận nghiệm của phương trình đã cho là số giao điểm của hai đồ thị.
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Hàm số lũy thừa, hàm số mũ và hàm số logarit hay, chi tiết
50 bài toán về hàm số lũy thừa, hàm số mũ, hàm số logarit và cách giải
Câu 30:
06/12/2024Tập nghiệm của bất phương trình là
 Xem đáp án
Xem đáp án
Đáp án đúng là A
Lời giải
![]()
*Phương pháp giải:
Xét bất phương trình có dạng:
- Nếu , tập nghiệm của bất phương trình là R, vì .
- Nếu thì bất phương trình tương đương với
+Với , nghiệm của bất phương trình là
+Với , nghiệm của bất phương trình là
*Lý thuyết:
• Khi giải bất phương trình mũ, ta cần chú ý đến tính đơn điệu của hàm số mũ.
Tương tự với bất phương trình dạng:
• Trong trường hợp cơ sốcó chứa ẩn số thì:
• Ta cũng thường sử dụng các phương pháp giải tương tự như đối với phương trình mũ:
+ Đưa về cùng cơ số.
+ Đặt ẩn phụ.
+ Sử dụng tính đơn điệu:
Hàm số y = f(x) nghịch biến trên D thì:
Hàm số y = f(x) đồng biến biến trên D thì:
Xem thêm
50 bài toán về bất phương trình mũ và cách giải (có đáp án 2024) – Toán 12
Bài thi liên quan
-
Bài tập Hàm số mũ, logarit cơ bản, nâng cao có lời giải (P1) (Đề 1)
-
30 câu hỏi
-
50 phút
-
-
Bài tập Hàm số mũ, logarit cơ bản, nâng cao có lời giải (P1) (Đề 3)
-
30 câu hỏi
-
50 phút
-
-
Bài tập Hàm số mũ, logarit cơ bản, nâng cao có lời giải (P1) (Đề 4)
-
25 câu hỏi
-
50 phút
-
-
Bài tập Hàm số mũ, logarit cơ bản, nâng cao có lời giải (P1) (Đề 5)
-
30 câu hỏi
-
50 phút
-
-
Bài tập Hàm số mũ, logarit cơ bản, nâng cao có lời giải (P1) (Đề 6)
-
30 câu hỏi
-
50 phút
-
-
Bài tập Hàm số mũ, logarit cơ bản, nâng cao có lời giải (P1) (Đề 7)
-
40 câu hỏi
-
50 phút
-
