Bài tập cuối chương 9 có đáp án
-
148 lượt thi
-
46 câu hỏi
-
40 phút
Danh sách câu hỏi
Câu 1:
21/07/2024Cho hai vectơ = (4; 3) và = (1; 7). Góc giữa hai vectơ và là:
A. 90°;
B. 60°;
C. 45o;
D. 30o.
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có
Vậy = 45o.
Câu 2:
18/07/2024Cho hai điểm M = (1; – 2) và N = (– 3; 4). Khoảng cách giữa hai điểm M và N là:
A. 4;
B. 6;
C. ;
D. .
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Ta có MN = = .
Câu 3:
01/07/2024Tam giác ABC có A = (– l; 1); B = (1; 3) và C = (1; –1).
Trong các phát biểu sau đây, phát biểu nào đúng?
A. ABC là tam giác có ba cạnh bằng nhau;
B. ABC là tam giác có ba góc đều nhọn;
C. ABC là tam giác cân tại B (có BA = BC);
D. ABC là tam giác vuông cân tại A.
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Xét tam giác ABC có:
⇒ AB = ;
⇒ BC =
⇒ AC =
Phát biểu A, C sai
Ta có:
⇒ = 90o = 90o
Vậy tam giác ABC vuông cân tại A. Do đó phát biểu D đúng và B sai.
Câu 4:
20/07/2024Cho phương trình tham số của đường thẳng
Trong các phương trình sau, phương trình nào là phương trình tổng quát của (d)?
A.
B.
C.
D.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Xét đường thẳng
Đường thẳng d đi qua M(5; – 9) có vectơ chỉ phương (1; – 2) và vectơ pháp tuyến
(2; 1).
Phương trình tổng quát của đường thẳng d là: 2(x – 5) + 1(y + 9) = 0 ⇔ 2x + y – 1 = 0.
Câu 5:
22/07/2024Đường thẳng đi qua điểm M(1; 0) và song song với đường thẳng d: 4x + 2y + 1 = 0 có phương trình tổng quát là:
A. 4x + 2y + 3 = 0;
B. 2x + y + 4 = 0;
C. 2x + y – 2 = 0;
D. x – 2y + 3 = 0.
 Xem đáp án
Xem đáp án
Lời giải
Đáp án đúng là: C
Gọi đường thẳng ∆ đi qua M(1; 0) và song song với đường thẳng d: 4x + 2y + 1 = 0 có phương trình tổng quát là 4x + 2y + c = 0 (c ≠ 1).
Vì M ∆ nên ta có: 4.1 + 2.0 + c = 0 ⇔ c = – 4 (thỏa mãn).
Vậy phương trình đường thẳng cần tìm là: 4x + 2y – 4 = 0 ⇔ 2x + y – 2 = 0.
Câu 6:
18/07/2024Bán kính của đường tròn tâm I(0; – 2) và tiếp xúc với đường thẳng là:
A. 15;
B. 5;
C. ;
D. 3.
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Đường tròn tâm I(0; – 2) và tiếp xúc với đường thẳng ∆: 3x – 4y – 23 = 0 có bán kính R = d(I, ∆) = .
Vậy bán kính đường tròn cần tìm là 3.
Câu 7:
15/07/2024Cho đường tròn (C): x2 + y2 + 2x + 4y – 20 = 0. Trong các mệnh đề sau đây, phát biểu nào sai?
A. (C) có tâm I(1; 2);
B. (C) có bán kính R = 5;
C. (C) đi qua điểm M(2; 2);
D. (C) không đi qua điểm A(1; 1). Xem đáp án
Xem đáp án
Đáp án đúng là: A
Đường tròn (C): x2 + y2 + 2x + 4y – 20 = 0 có a = – 1; b = – 2; c = – 20
Suy ra đường tròn (C) có tâm I(– 1; – 2); bán kính R = .
Phát biểu A sai, phát biểu B đúng.
Thay điểm M(2; 2) vào phương trình đường tròn (C) ta có: 22 + 22 + 2.2 + 4.2 – 20 = 0 thoả mãn phương trình đường tròn. Suy ra (C) đi qua điểm M
Phát biểu C đúng.
Thay điểm A(1; 1) vào phương trình đường tròn (C) ta có: 12 + 12 + 2.1 + 4.1 – 20 = – 12 ≠ 0 không thoả mãn phương trình đường tròn. Suy ra (C) không đi qua điểm A
Phát biểu D đúng.
Vậy đáp án đúng là A.
Câu 8:
17/07/2024Phương trình tiếp tuyến tại điểm M(3; 4) với đường tròn (C):là:
A. ;
B. ;
C. ;
D. .
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có 32 + 42 – 2.3 – 44 – 3 = 0 nên điểm M thuộc đường tròn (C)
Đường tròn (C) có tâm I(1; 2)
Phương trình tiếp tuyến của d với (C) tại điểm M(3; 4)
(1 – 3)(x – 3) + (2 – 4)(y – 4) = 0
⇔ – 2x – 2y + 14 = 0
⇔ x + y – 7 = 0.
Câu 9:
21/07/2024Phương trình chính tắc của elip có hai đỉnh là (–3; 0); (3; 0) và hai tiêu điểm là (–1; 0); (1; 0) là:
A.
B.
C.
D.
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có a = 3; c = 1 suy ra b = a2 – c2 = 32 – 12 = 8.
Phương trình chính tắc của Elip là: .
Câu 10:
08/07/2024Phương trình chính tắc của hypebol có hai đỉnh là (– 4; 0); (4; 0) và hai tiêu điểm là (– 5; 0); (5; 0) là:
A.
B.
C.
D.
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có a = 4; c = 5 suy ra
Vậy phương trình chính tắc của Hypebol là:
Câu 11:
15/07/2024Phương trình chính tắc của parabol có tiêu điểm (2; 0) là:
A. y2 = 8x;
B. y2 = 4x;
C. y2 = 2x;
D. y = 2x2.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có tiêu điểm suy ra p = 4
Vậy phương trình chính tắc của parabol là: y2 = 8x.
Câu 12:
22/07/2024Elip với độ dài hai trục là 20 và 12 có phương trình chính tắc là:
A.
B.
C.
D.
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Elip có độ dài hai trục lần lượt là:
Trục lớn 2a = 20 ⇒ a = 10;
Trục bé 2b = 12 ⇒ b = 6.
Vậy phương trình chính tắc của Elip là:
Câu 13:
03/07/2024Trong mặt phẳng Oxy cho ba điểm A(2; 2); B(1; 3); C(– 1; 1).
a) Chứng minh OABC là một hình chữ nhật;
 Xem đáp án
Xem đáp án
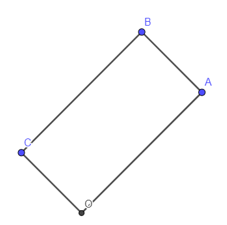
nên hai vectơ cùng phương hay OA song song với BC và OA = BC = .
Do đó tứ giác OABC là hình bình hành.
Ta có hay OA OC
Tứ giác OABC là hình bình hành và có 1 góc vuông nên tứ giác OABC là hình chữ nhật.
Câu 14:
18/07/2024b) Tìm toạ độ tâm I của hình chữ nhật OABC.
 Xem đáp án
Xem đáp án
b) Tâm I(x; y) của hình chữ nhật OABC là trung điểm của OB
Ta có
Vậy .
Câu 15:
03/07/2024Tìm góc giữa hai đường thẳng d1 và d2.
a) và ;
 Xem đáp án
Xem đáp án
Hai đường thẳng d1 và d2 có các vectơ pháp tuyến lần lượt là = (5; – 9); = (9; 5)
Ta có = 5.9 + (– 9).5 = 0
Vậy (d1, d2) = 90o.
Câu 16:
22/07/2024b) và ;
 Xem đáp án
Xem đáp án
b) và ;
Hai đường thẳng d1 và d2 có các vectơ pháp tuyến lần lượt là = (2; - 1); = (1; -3)
Ta có
Vậy (d1, d2) = 45o
Câu 17:
21/07/2024Cho tam giác ABC với toạ độ ba đỉnh là A(1; 1); B(3; l); C(1; 3). Tính độ dài đường cao AH.
 Xem đáp án
Xem đáp án
Ta có phương trình đường thẳng BC đi qua điểm B(3; 1) có vectơ chỉ phương là vectơ và có vectơ pháp tuyến là vectơ
(1; 1)
Phương trình tổng quát của BC là: (x – 3) + (y – 1) = 0 ⇔ x + y – 4 = 0.
Đường cao AH đi qua điểm A(1; 1) có véc tơ pháp tuyến là vectơ (– 2; 2) có phương trình là: – 2(x – 1) + 2(y – 1) = 0 ⇔ – x + y = 0.
Toạ độ điểm H là giao điểm của đường thẳng AH và đường thẳng BC ta có hệ
.
Suy ra toạ độ điểm H(2; 2)
Ta có AH = .
Vậy độ dài đường cao AH là .
Câu 18:
20/07/2024Tính bán kính của đường tròn tâm J(1; 0) và tiếp xúc với đường thẳng
 Xem đáp án
Xem đáp án
Bán kính của đường tròn tâm J(1; 0) và tiếp xúc với đường thẳng d: 8x – 6y + 22 = 0 là R = d(J, d) = .
Vậy bán kính của đường tròn đã cho là 3.
Câu 19:
20/07/2024Tính khoảng cách giữa hai đường thẳng:
và (biết ∆ // ∆’).
 Xem đáp án
Xem đáp án
Lấy điểm M(0; ) ∈ ∆. Vì ∆ // ∆’ nên M ∉ ∆’.
Khi đó khoảng cách giữa hai đường thẳng ∆ và ∆’ bằng khoảng cách từ điểm M đến đường thẳng ∆’ và bằng:
d(∆, ∆’) = d(M,∆’).
Câu 20:
09/07/2024Tìm tâm và bán kính của các đường tròn có phương trình:
a) (x + 1)2 + (y + 2)2 = 225;
 Xem đáp án
Xem đáp án
a) (x + 1)2 + (y + 2)2 = 225 ⇔ (x + 1)2 + (y + 2)2 = 152
Vì vậy đường tròn có tâm I(– 1; – 2), bán kính R = 15.
Câu 21:
25/06/2024b) x2 + (y – 7)2 = 5;
 Xem đáp án
Xem đáp án
b) x2 + (y – 7)2 = 5 ⇔ x2 + (y – 7)2 =
Vì vậy đường tròn có tâm I(0; 7), bán kính R = .
Câu 22:
04/07/2024c) x2 + y2 – 10x – 24y = 0.
 Xem đáp án
Xem đáp án
c) x2 + y2 – 10x – 24y = 0 ⇔ x2 + y2 – 2.5x – 2.12.y = 0
Phương trình đường tròn có dạng x2 + y2 – 2ax – 2by + c = 0 với a = 5; b = 12; c = 0
Ta có R2 = a2 + b2 – c = 25 + 144 – 0 = 169 ⇒ R = .
Vậy đường tròn có tâm I(5; 12) bán kính R = 13.
Câu 23:
23/07/2024Lập phương trình đường tròn trong các trường hợp sau:
a) Có tâm I(2; 2) và bán kính bằng 7;
 Xem đáp án
Xem đáp án
a) Đường tròn tâm I(2; 2) và bán kính bằng 7 có phương trình:
(x – 2)2 + (y – 2)2 = 49.
Vậy phương trình đường tròn là (x – 2)2 + (y – 2)2 = 49.
Câu 24:
25/06/2024b) Có tâm J( 0; -3) và đi qua điểm M(-2; -7);
 Xem đáp án
Xem đáp án
b) Đường tròn tâm J(0; - 3) đi qua điểm M(- 2; - 7) có bán kính R = JM
Ta có JM =
Đường tròn tâm J(0; - 3) bán kính R = có phương trình là
(x – 0)2 + (y + 3)2 = 20 x2 + (y + 3)2 = 20
Câu 25:
11/07/2024c) Đi qua hai điểm A(2; 2); B(6; 2) và có tâm nằm trên đường thẳng x - y = 0;
 Xem đáp án
Xem đáp án
c) Gọi tâm I(a; b) vì tâm I thuộc đường thẳng x – y = 0 nên ta có a – b = 0 a = b
Vậy tâm I(a; a)
Đường tròn đi qua hai điểm A(2; 2); B(6; 2) nên ta có AI2 = BI2
(a – 2)2 + (a – 2)2 = (a – 6)2 + (a – 2)2
a2 – 4a + 4 = a2 – 12a + 36
8a = 32
a = 4
Vậy tâm I(4; 4)
Ta có bán kính R = IA =
Phương trình đường tròn tâm I(4; 4) bán kính R = có phương trình
(x – 4)2 +(y – 4)2 = 8
Câu 26:
11/07/2024d) Đi qua gốc toạ độ và cắt hai trục toạ độ tại các điểm có hoành độ là 8; tung độ là 6.
 Xem đáp án
Xem đáp án
d) Phương trình đường tròn đi qua O(0; 0); A(8; 0); B(0; 6)
Gọi tâm I(a; b)
Vì đường tròn đi qua 3 điểm O, A, B nên ta có
Vậy tâm I(4; 3)
Bán kính R = OI =
Phương trình đường tròn tâm I(4; 3) bán kính R = 5 có phương trình
(x – 4)2 +(y – 3)2 = 25
Câu 27:
13/07/2024Viết phương trình tiếp tuyến với đường tròn tại điểm A(4; 5).
 Xem đáp án
Xem đáp án
Ta thay toạ độ điểm A vào phương trình đường tròn (C): (4 – 1)2 + (5 – 1)2 = 25. Suy ra A thuộc đường tròn (C)
Đường tròn (C) có tâm I(1; 1)
Phương trình tiếp tuyến tại của đường tròn (C) tại A là
(1 – 4)(x – 4) + (1 – 5)(x – 5) = 0 ⇔ – 3x – 4y + 32 = 0.
Câu 28:
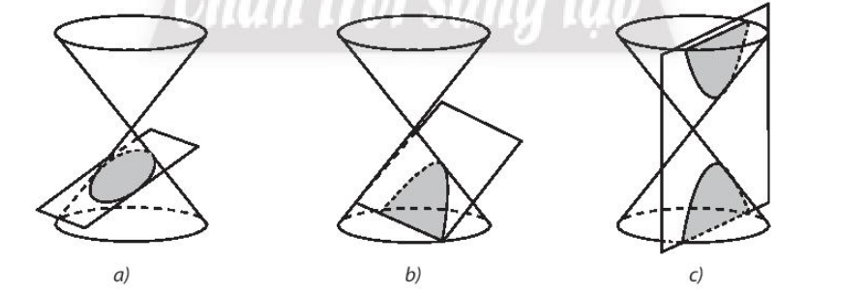
19/07/2024Gọi tên các đường conic sau:
 Xem đáp án
Xem đáp án
a) Hình vẽ đã cho biểu diễn đường Elip.
b) Hình vẽ đã cho biểu diễn đường Parabol.
c) Hình vẽ đã cho biểu diễn đường Hypebol.
Câu 29:
22/07/2024Viết phương trình chính tắc của elip thoả mãn các điều kiện sau:
a) Độ đài trục lớn 26; độ dài trục nhỏ 10;
 Xem đáp án
Xem đáp án
Lời giải
a) Ta có 2a = 26 ⇒ a = 13; 2b = 10 ⇒ b = 5.
Suy ra phương trình chính tắc của Elip là: .
Vậy phương trình chính tắc của Elip là: .
Câu 30:
06/07/2024b) Độ dài trục lớn 10; tiêu cự 6.
 Xem đáp án
Xem đáp án
b) Ta có 2a = 10 ⇒ a = 5; 2c = 6 ⇒ c = 3 và b =
Suy ra phương trình chính tắc của Elip là: .
Vậyphương trình chính tắc của Elip là: .
Câu 31:
02/07/2024Tìm toạ độ các tiêu điểm; toạ độ các đỉnh; độ đài trục thực và trục ảo của các hypebol sau:
a)
 Xem đáp án
Xem đáp án
a)
Suy ra a = 5; b = 12 và .
Toạ độ các đỉnh A1(- 5; 0); A2(5; 0)
Tiêu điểm F1(- 13; 0); F2(13; 0)
Độ dài trục thực 2a = 10; độ dài trục ảo 2b = 24.
Câu 32:
17/07/2024b)
 Xem đáp án
Xem đáp án
b)
Suy ra a = 4; b = 3 và
Khi đó:
Toạ độ các đỉnh A1(- 4; 0); A2(4; 0);
Tiêu điểm F1(- 5; 0); F2(5; 0).
Độ dài trục thực 2a = 8; độ dài trục ảo 2b = 6.
Câu 33:
22/07/2024Viết phương trình chính tắc của hypebol thoả mãn các điều kiện sau:
a) Đỉnh (-6; 0) và (6; 0); tiêu điểm (-10; 0) và (10; 0);
 Xem đáp án
Xem đáp án
a) Ta có các đỉnh A1(- 6; 0); A2(6; 0) a = 6
Các tiêu điểm F1(- 10; 0); F2(10; 0) c = 10
b =
Khi đó phương trình chính tắc của Hypebol là: .
Vậy phương trình chính tắc của Hypebol là: .
Câu 34:
13/07/2024b) Độ dài trục thực là 10; độ dài trục ảo là 20.
 Xem đáp án
Xem đáp án
b) Ta có:
Độ dài trục thực 2a = 10 a = 5;
Độ dài trục ảo 2b = 20 b = 10.
Khi đó phương trình chính tắc của Hypebol là: .
Vậy phương trình chính tắc của Hypebol là: .
Câu 35:
21/07/2024Tìm toạ độ tiêu điểm, phương trình đường chuẩn của các parabol sau:
a) y2 = 4x;
 Xem đáp án
Xem đáp án
a) Xét parabol y2 = 4x
Ta có 2p = 4 ⇔ p = 2 suy ra tiêu điểm F(1; 0) và đường chuẩn ∆: x + 1 = 0.
Câu 36:
26/06/2024b) y2 = 2x;
 Xem đáp án
Xem đáp án
b) Xét parabol y2 = 2x
Ta có 2p = 2 ⇔ p = 1 suy ra tiêu điểm và đường chuẩn ∆: .
Câu 37:
20/07/2024c) y2 = – 6x.
 Xem đáp án
Xem đáp án
c) Xét parabol y2 = – 6x
Ta có 2p = – 6 ⇔ p = – 3 suy ra tiêu điểm và đường chuẩn ∆: .
Câu 38:
03/07/2024Viết phương trình chính tắc của parabol thoả mãn các điều kiện:
a) Tiêu điểm (8; 0);
 Xem đáp án
Xem đáp án
a) Ta có tiêu điểm F(8; 0) nên ⇒ p = 16
Vì vậy phương trình chính tắc của Parabol: y2 = 32x.
Câu 39:
17/07/2024b) Khoảng cách từ tiêu điểm đến đường chuẩn bằng 4.
 Xem đáp án
Xem đáp án
b) Ta có khoảng cách từ tiêu điểm đến đường chuẩn bằng 4 nên p = 4
Vì vậy phương trình chính tắc của Parabol: y2 = 8x.
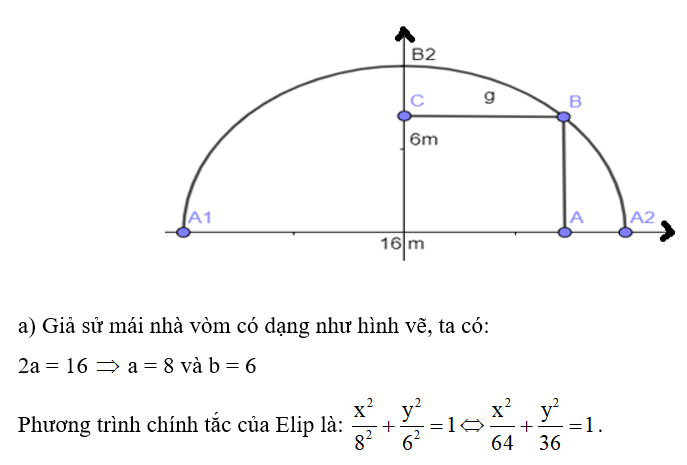
Câu 41:
04/07/2024b) Tính khoảng cách thẳng đứng từ một điểm cách chân vách 4 m lên đến mái vòm.
 Xem đáp án
Xem đáp án
b) Gọi điểm A là điểm có khoảng cách 4m từ chân vách nên OA = 8 – 4 = 4 m. Từ điểm A dõng lên cắt mái vòm tại B khi đó B(4; y).
Suy ra độ dài AB là khoảng cách từ chân vách đến mái vòm và bằng y.
Vì B thuộc Elip nên ta có .
Vậy khoảng cách từ điểm cách chân vách 4m lên đến mái vòm là ≈ 5,2 m.
Câu 42:
15/07/2024Cho biết Mặt Trăng chuyển động quanh Trái Đất theo quỹ đạo là elip (E) với Trái Đất là một tiêu điểm. Cho biết độ dài hai trục của (E) là 768800 km và 767619 km. Viết phương trình chính tắc của elip (E).
 Xem đáp án
Xem đáp án
Ta có:
2a = 768800 a = 384400;
2b = 767619 b = .
Khi đó phương trình chính tắc của Elip là: .
Câu 43:
18/07/2024Gương phản chiếu của một đèn pha có mặt cắt là một parabol (P) với tim bóng đèn đặt ở tiêu điểm F. Chiều rộng giữa hai mép gương là 50 cm; chiều sâu của gương là 40 cm. Viết phương trình chính tắc của (P).
 Xem đáp án
Xem đáp án
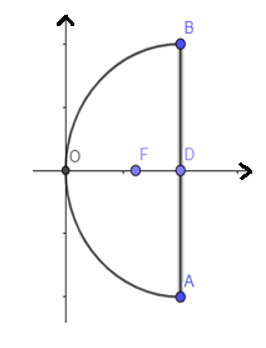
Ta có OD = 40 cm; AB = 50 cm
Gọi phương trình chính tắc của parabol là y2 = 2px
Dựa vào hình vẽ ta có khi x = 40 thì y = 25
252 = 2.p.40 p =
Phương trình chính tắc của parabol là: y2 = x.
Câu 44:
21/07/2024Màn hình của rađa tại trạm điều khiển không lưu được thiết lập hệ toạ độ Oxy với vị trí trạm có toạ độ O(0; 0) và rađa có bán kính hoạt động là 600 km. Một máy bay khởi hành tử sân bay lúc 8 giờ. Cho biết sau t giờ máy bay có toạ độ: .
a) Tìm toạ độ máy bay lúc 9 giờ;
 Xem đáp án
Xem đáp án
a) Máy bay khởi hành lúc 8 giờ vậy lúc 9 giờ máy bay bay được 1 giờ hay t = 1 nên toạ độ của máy báy là:
Vậy toạ độ máy bay lúc 9 giờ là: A(181; – 179).
Câu 45:
15/07/2024b) Tính khoảng cách giữa máy bay và trạm điều khiển không lưu;
 Xem đáp án
Xem đáp án
b) Khoảng cách giữa máy bay và trạm không điều khiển bằng OA
Ta có OA = 255 km.
Vậy khoảng cách giữa máy bay và trạm không điều khiển khoảng 255 km.
Câu 46:
23/07/2024c) Lúc mây giờ máy bay ra khỏi tầm hoạt động của rađa?
 Xem đáp án
Xem đáp án
c) Sau t giờ máy bay có toạ độ:
Hay toạ độ máy bay sau t giờ là: B(1 + 180t; 1 – 180t).
Để máy bay ra khỏi tầm hoạt động của rađa thì OB > 600 km ⇔ OB2 > 6002
Ta có OB2 = (xB – xO)2 + (yB – yO)2 = (1 + 180t)2 + (1 – 180t)2 > 6002
⇔ 32400t2 + 360t +1 + 32400t2 – 360t +1 > 6002
⇔ 64800t2 – 359998 > 0
⇒ |t| > 2,36
Mà t > 0 nên t > 2,36
Ta lại có 2,36 giờ ≈ 2 giờ 22 phút.
Vậy lúc khoảng 10 giờ 22 phút trở đi máy bay ra khỏi tầm hoạt động của rađa.
Có thể bạn quan tâm
- Trắc nghiệm Toán 10 Bài tập cuối chương IX có đáp án (269 lượt thi)
- Trắc nghiệm Toán 10 CTST Bài tập cuối chương 9 (Phần 2) có đáp án (547 lượt thi)
Các bài thi hot trong chương
- Trắc nghiệm Toán 10 CTST Bài 2. Đường thẳng trong mặt phẳng tọa độ (Phần 2) có đáp án (928 lượt thi)
- Trắc nghiệm Toán 10 CTST Bài 1. Tọa độ của vectơ (Phần 2) có đáp án (670 lượt thi)
- Trắc nghiệm Toán 10 CTST Bài 4: Ba đường conic trong mặt phẳng tọa độ (Phần 2) có đáp án (630 lượt thi)
- Trắc nghiệm Toán 10 CTST Bài 3: Đường tròn trong mặt phẳng tọa độ (Phần 2) có đáp án (464 lượt thi)
- Trắc nghiệm Toán 10 Bài 3. Đường tròn trong mặt phẳng tọa độ có đáp án (448 lượt thi)
- Trắc nghiệm Toán 10 Bài 2. Đường thẳng trong mặt phẳng tọa độ có đáp án (364 lượt thi)
- Trắc nghiệm Toán 10 Bài 4. Ba đường conic trong mặt phẳng tọa độ có đáp án (289 lượt thi)
- Trắc nghiệm Toán 10 Bài 1. Tọa độ của vectơ có đáp án (223 lượt thi)