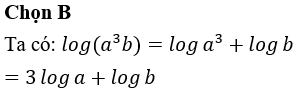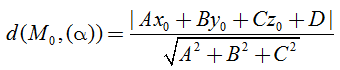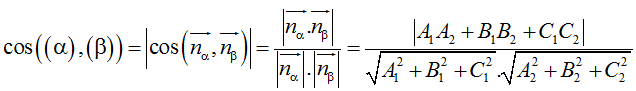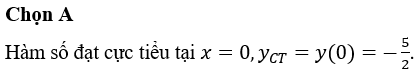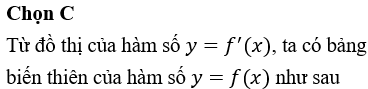5 Đề thi thử thpt quốc gia môn Toán cực hay có lời giải chi tiết
5 Đề thi thử thpt quốc gia môn Toán cực hay có lời giải chi tiết (Đề số 2)
-
516 lượt thi
-
50 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 2:
18/11/2024Trong không gian Oxyz, mặt phẳng (Oxy) có phương trình là
 Xem đáp án
Xem đáp án
Đáp án đúng: D
*Lời giải:

*Phương pháp giải:
Mặt phẳng (Oxy) là tập hợp các điểm có cao độ z = 0 nên có phương trình: z = 0.
*Cách giải và các dạng bài toán về hệ trục tọa độ trong không gian:
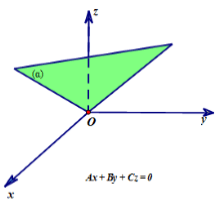
Phương trình tổng quát của mặt phẳng
- Trong không gian Oxy , mọi mặt phẳng đều có dạng phương trình:
Ax + By + Cz + D = 0 với A2 + B2 + C2 ≠ 0
- Nếu mặt phẳng (α) có phương trình Ax + By + Cz + D = 0 thì nó có một VTPT là n→(A; B; C).
- Phương trình mặt phẳng đi qua điểm Mo(xo; yo; zo) và nhận vectơ n→(A; B; C) khác 0→ là VTPT là: A(x - xo) + B(y - yo) + C(z - zo) = 0 .
• Các trường hợp riêng
Xét phương trình mặt phẳng (α): Ax + By + Cz + D = 0 với A2 + B2 + C2 ≠ 0
- Nếu D = 0 thì mặt phẳng (α) đi qua gốc tọa độ O.
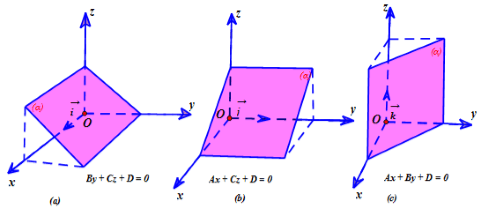
- Nếu A = 0, B ≠ 0, C ≠ 0 thì mặt phẳng (α) song song hoặc chứa trục Ox.
- Nếu A ≠ 0, B = 0, C ≠ 0 thì mặt phẳng (α) song song hoặc chứa trục Oy.
- Nếu A ≠ 0, B ≠ 0, C = 0 thì mặt phẳng (α) song song hoặc chứa trục Oz.
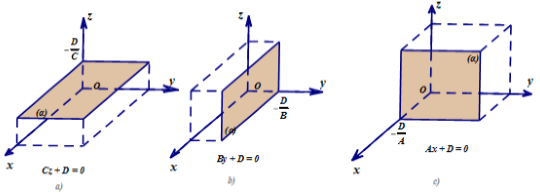
- Nếu A = B = 0, C ≠ 0 thì mặt phẳng (α) song song hoặc trùng với (Oxy).
- Nếu A = C = 0, B ≠ 0 thì mặt phẳng (α) song song hoặc trùng với (Oxz).
- Nếu B = C = 0, A ≠ 0 thì mặt phẳng (α) song song hoặc trùng với (Oyz).
Chú ý:
- Nếu trong phương trình (α) không chứa ẩn nào thì (α) song song hoặc chứa trục tương ứng.
- Phương trình mặt phẳng theo đoạn chắn (α): 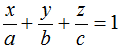
Khoảng cách từ một điểm đến một mặt phẳng.
• Trong không gian Oxyz, cho điểm Mo(xo; yo; zo) và mặt phẳng (α): Ax + By + Cz + D = 0
Khi đó khoảng cách từ điểm Mo đến mặt phẳng (α) được tính:
Góc giữa hai mặt phẳng
Trong không gian Oxyz, cho hai mặt phẳng (α): A1x + B1y + C1z + D1 = 0 và (β): A2x + B2y + C2z + D2 = 0
Góc giữa (α) và (β) bằng hoặc bù với góc giữa hai VTPT nα→, nβ→. Tức là:
Một số dạng bài tập về viết phương trình mặt phẳng
Dạng 1: Viết phương trình mặt phẳng khi biết một điểm và vectơ pháp tuyến của nó.
Áp dụng cách viết phương trình mặt phẳng đi qua 1 điểm và có 1 VTPT.
Dạng 2: Viết phương trình mặt phẳng (α) đi qua 1 điểm Mo(xo; yo; zo) và song song với 1 mặt phẳng (β): Ax + By + Cz + D = 0 cho trước.
Cách 1: Thực hiện theo các bước sau:
1. VTPT của (β) là nβ→ = (A; B; C)
2. (α) // (β) nên VTPT của mặt phẳng (α) là nα→ = nβ→ = (A; B; C)
3. Phương trình mặt phẳng (α): A(x - x0) + B(y - y0) + C(z - z0) = 0
Cách 2:
1. Mặt phẳng (α) // (β) nên phương trình (P) có dạng: Ax + By + Cz + D' = 0 (*), với D' ≠ D.
2. Vì (P) qua 1 điểm Mo(xo; yo; zo) nên thay tọa độ Mo(xo; yo; zo) vào (*) tìm được D'.
Dạng 3: Viết phương trình mặt phẳng (α) đi qua 3 điểm A, B, C không thẳng hàng.
1. Tìm tọa độ các vectơ: AB→, AC→
2. Vectơ pháp tuyến của (α) là: nα→ = [AB→, AC→]
3. Điểm thuộc mặt phẳng: A (hoặc B hoặc C).
4. Viết phương trình mặt phẳng qua 1 điểm và có VTPT nα
Dạng 4: Viết phương trình mặt phẳng (α) đi qua điểm M và vuông góc với đường thẳng Δ
1. Tìm VTCP của Δ là uΔ→
2. Vì (α) ⊥ Δ nên (α) có VTPT nα→ = uΔ→
3. Áp dụng cách viết phương trình mặt phẳng đi qua 1 điểm và có 1 VTPT nα→
Dạng 5: Viết phương trình mặt phẳng (α) chứa đường thẳng Δ, vuông góc với mặt phẳng (β)
1. Tìm VTPT của (β) là nβ→
2. Tìm VTCP của Δ là uΔ→
3. VTPT của mặt phẳng (α) là: nα→ = [nβ→; uΔ→]
4. Lấy một điểm M trên Δ
5. Áp dụng cách viết phương trình mặt phẳng đi qua 1 điểm và có 1 VTPT.
Dạng 6: Viết phương trình mặt phẳng (α) qua hai điểm A, B và vuông góc với mặt phẳng (β)
1. Tìm VTPT của (β) là nβ→
2. Tìm tọa độ vectơ AB→
3. VTPT của mặt phẳng (α) là: nα→ = [nβ→, AB→]
4. Áp dụng cách viết phương trình mặt phẳng đi qua 1 điểm và có 1 VTPT.
Xem thêm các bài viết liên quan hay, chi tiết
Lý thuyết Hệ trục toạ độ trong không gian– Toán lớp 12 Kết nối tri thức
Câu 11:
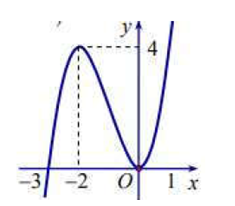
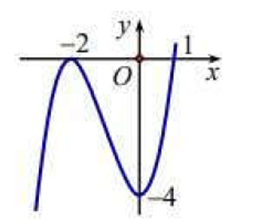
14/07/2024Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây
 Xem đáp án
Xem đáp án
Chọn B
Từ đồ thị ta thấy đây là đồ thị của hàm số bậc ba có hệ số a>0
Vậy đáp án B đúng
Câu 17:
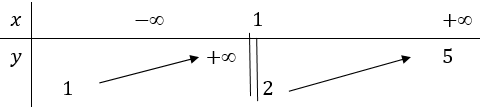
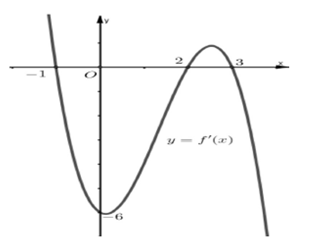
14/07/2024Cho hàm số f(x) có đạo hàm f'(x)=,∀x∈R. Số điểm cực trị của hàm số đã cho là
 Xem đáp án
Xem đáp án
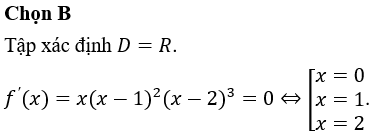
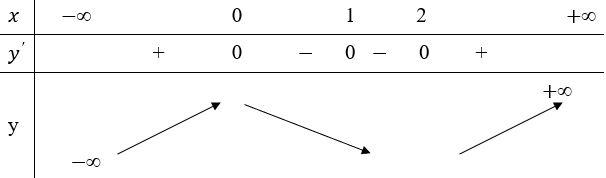
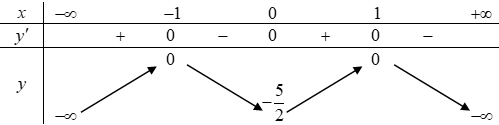
Vậy hàm số đã cho có hai điểm cực trị.
Câu 31:
14/07/2024Ông A vay ngân hàng 200 triệu đồng với lãi suất 1%/tháng. Ông ta muốn hoàn nợ cho ngân hàng theo cách sau: Sau đúng một tháng kể từ ngày vay, ông bắt đầu hoàn nợ, hai lần hoàn nợ liên tiếp cách nhau đúng một tháng, số tiền hoàn nợ mỗi tháng là như nhau. Biết rằng mỗi tháng ngân hàng chỉ tính lãi trên số dư nợ thực tế của tháng đó và sau đúng hai năm kể từ ngày vay ông A trả hết nợ. Hỏi số tiền mỗi tháng ông ta cần trả cho ngân hàng gần nhất với số tiền nào dưới đây?
 Xem đáp án
Xem đáp án
Chọn D
Vay vốn trả góp: Vay ngân hàng số tiền là P đồng với lãi suất r% trên tháng. Sau đúng một tháng kể từ ngày vay, bắt đầu hoàn nợ; hai lần hoàn nợ cách nhau đúng một tháng, mỗi tháng hoàn nợ số tiền là X đồng và trả hết số tiền nợ sau đúng n tháng


Câu 32:
20/07/2024Từ các số 1, 2, 3, 4, 5, 6, 7 lập được bao nhiêu số tự nhiên có sáu chữ số đôi một khác nhau trong đó các chữ số 1, 2, 3 luôn có mặt và đứng cạnh nhau
 Xem đáp án
Xem đáp án
Chọn C
Ta xem 3 chữ số 1; 2; 3 đứng cạnh nhau là một phần tử X.
Chọn ra 3 chữ số còn lại có cách chọn.
Xếp phần tử X và 3 chữ số vừa chọn ta có: 4! Cách.
Các chữ số 1;2;3 trong X có thể hoán vị cho nhau có: 3! Cách.
Vậy có tất cả (số)
Câu 37:
20/07/2024Xếp ngẫu nhiên tám học sinh gồm bốn học sinh nam (trong đó có Hoàng và Nam) cùng bốn học sinh nữ (trong đó có Lan) thành một hàng ngang. Xác suất để trong tám học sinh trên không có hai học sinh cùng giới đúng cạnh nhau, đồng thời Lan đứng cạnh Hoàng và Nam là
 Xem đáp án
Xem đáp án
Chọn D
Xếp ngẫu nhiên 8 học sinh có 8! cách.
"Buộc" Hoàng, Lan, Nam thành một nhóm. Khi đó vì hai bên nhóm này bắt buộc là nữ nên ta xem nhóm ba người này là một nam. Vậy có ba nam và ba nữ.
Trường hợp 1: nam ngồi vị trí lẻ.
Xếp 3 nam vào 3 vị trí lẻ: 3!
Xếp 3 nữ vào 3 vị trí chẵn: 3!
Hoán vị hai học sinh nam trong nhóm: 2!
Suy ra số cách xếp trong trường hợp này là: 3!.3!.2!=72 cách
Trường hợp 2: nam ngồi vị trí chẵn
Tương tự có 72 cách
Vậy có cách xếp tám học sinh không có hai học sinh cùng giới đứng cạnh nhau, đồng thời Lan đứng cạnh Hoàng và Nam.
Suy ra xác suất cần tìm là .
Bài thi liên quan
-
5 Đề thi thử thpt quốc gia môn Toán cực hay có lời giải chi tiết (Đề số 1)
-
50 câu hỏi
-
50 phút
-
-
5 Đề thi thử thpt quốc gia môn Toán cực hay có lời giải chi tiết (Đề số 3)
-
50 câu hỏi
-
50 phút
-
-
5 Đề thi thử thpt quốc gia môn Toán cực hay có lời giải chi tiết (Đề số 4)
-
50 câu hỏi
-
50 phút
-
-
5 Đề thi thử thpt quốc gia môn Toán cực hay có lời giải chi tiết (Đề số 5)
-
50 câu hỏi
-
50 phút
-