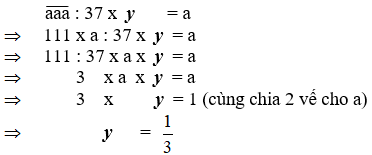28 Đề ôn thi vào lớp 6 môn Toán cực hay (Đề số 12)
-
12205 lượt thi
-
6 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 3:
22/07/2024Tổng của ba số là 2011. Số thứ nhất lớn hơn tổng của số thứ hai và số thứ ba là 123 đơn vị. Nếu bớt số thứ hai đi 44 đơn vị thì số thứ hai bằng số thứ ba. Hãy tìm ba số đó?
Xem đáp án
Ta có sơ đồ:
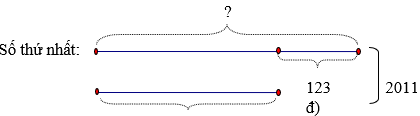
Số thứ hai và số thứ ba:
Số thứ nhất là: (2011 + 123 ) : 2 = 1067
Tổng của số thứ hai và số thứ ba là: 1067 - 123 = 944
Số thứ hai:
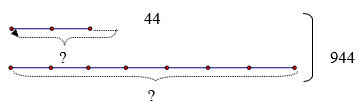
Số thứ ba:
Tổng số phần bằng nhau là: 7 + 2 = 9 (phần)
Số thứ hai là: ( 944 – 44) : 9 2 + 44 = 244
Số thứ ba là: 944 - 244 = 700
Đáp số: Ba số lần lượt là: 1067; 244 và 700
Câu 4:
22/07/2024Một cửa hàng trong ngày khai trương đã hạ giá 15% giá định bán đối với mọi thứ hàng hóa nhưng cửa hàng đó vẫn lãi được 2% so với giá mua mỗi loại hàng hóa. Hỏi nếu không hạ giá thì cửa hàng đó lãi bao nhiêu phần trăm so với giá mua?
Xem đáp án
- Giả sử tiền vốn của một món hàng là 100 đồng
thì trong ngày khai trương món hàng đó bán với số tiền là:
100 + 100 x 2% = 102 (đồng) (0,5 đ)
- Giá bán nhân ngày khai trương so với giá định bán
chiếm số phần trăm là:
100% - 15% = 85% (giá định bán). (0,5 đ)
- Vậy theo giá định bán thì món hàng đó bán với số tiền là:
102 : 85% = 120 (đồng) (0,5 đ)
- Theo giá định bán thì món hàng đó bán được số tiền lãi là:
120 – 100 = 20 (đồng) (0,25 đ)
- Theo giá định bán thì cửa hàng đó bán lãi
số phần trăm so với giá mua là:
20 : 100 = 20% (0,25 đ)
Đáp số: 20%
Câu 5:
22/07/2024Đoạn đường từ A đến B gồm một đoạn lên đốc và một đoạn nằm ngang. Một người đi từ A đến B hết 2 giờ và trở về từ B về A hết 1giờ 10 phút. Tính quãng đường AB. Biết vận tốc đi lên dốc là 8km/giờ; vận tốc đi xuống dốc là 18km/giờ còn vận tốc đi trên đoạn nằm ngang là 12km/giờ.
Xem đáp án
- Vì đi và về trên đoạn đường nằm ngang không thay đổi vận tốc
nên thời giạn đi trên đoạn đường nằm ngang đó cũng không thay đổi.
Sự chênh lệch thời gian của đi và về chính là thời gian của lên dốc và xuống dốc. (0,25 đ)
Thời gian lên dốc nhiều hơn thời gian xuống dốc là:
2giờ - 1giờ 10 phút = 50 phút giờ. (0,25 đ)
- Tỉ số giữa vận tốc lên dốc và vận tốc xuống dốc là:
- Vì quãng đường lên dốc khi đi cũng chính là quãng đường xuống dốc khi về
nên thời gian tỉ lệ nghịch với vận tốc.
Vậy tỉ số giữa thời gian lên dốc và thời gian xuống dốc là:
Đáp số: 18 km
Câu 6:
22/07/2024Cho tam giác MNP. Trên cạnh MP lấy điểm K sao cho trên cạnh MN lấy điểm I sao choNối NK và PI cắt nhau tại O.
a. So sánh diện tích tam giác MNK và KNP.
b. So sánh diện tích tam giác IKN và MNK.
c. Biết IP = 24cm. Tính độ dài đoạn IO và OP.
Xem đáp án
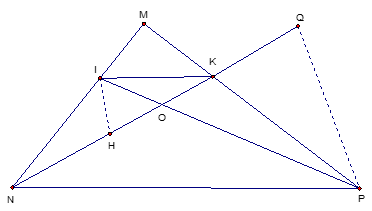
a. So sánh diện tích tam giác MNK và KNP: (0,5 điểm)
* Xét 2 tam giác MNK và KNP, có:
b. So sánh diện tích tam giác IKN và MNK: (0,5 điểm)
* Xét 2 tam giác giác IKN và MNK, có:
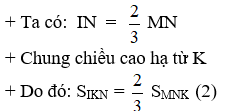
c. Tính độ dài đoạn IO và OP: (1,5 điểm)
- Vẽ đường cao IH và PQ.