25 câu hỏi trắc nghiệm thuộc 200 Bài tập nguyên hàm tích phân cơ bản, nâng cao (P1) (Đề 5)

Câu 1:

13/07/2024

Thể tích V của khối tròn xoay thu được khi quay xung quanh trục Ox hình phẳng giới hạn bởi các đường $y = x \sqrt{\ln x}, x = e$ và trục hoành là

Xem đáp án

Đáp án A.

Câu 2:

14/07/2024

Cho f(x), f(-x) liên tục trên R và thỏa mãn $2 f (x) + 3 f (- x) = \frac{1}{x^{2} + 4}$ Tính $I = \int_{- 2}^{2} f (x) d x$ .

Xem đáp án

Đáp án A.

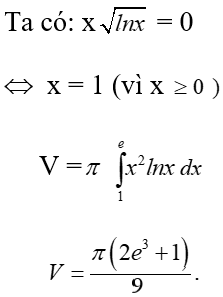
Câu 3:

17/07/2024

Cho hàm số y=f(x) liên tục trên R và hàm số y=g(x)= $x . f (x^{2})$ có đồ thị trên đoạn [0;2] như hình vẽ bên. Biết diện tích S của miền được tô đậm bằng $\frac{5}{2}$ tính tích phân $I = \int_{1}^{4} f (x) d x$

Xem đáp án

Đáp án C.

Câu 4:

17/07/2024

Cho hàm số y=f(x) liên tục trên R Biết rằng $\int_{1}^{e^{3}} \frac{f (\ln x)}{x} d x = 7, \int_{0}^{\frac{π}{2}} f (\cos x) \sin x d x = 3$ .Tính tích phân $I = \int_{1}^{3} (f (x) + 2 x) d x$

Xem đáp án

Đáp án B.

Câu 5:

14/07/2024

Tìm giá trị của a để $I = \int_{1}^{a} \frac{x^{3} - 2 \ln x}{x^{2}} d x = \frac{1}{2} + \ln 2$

Xem đáp án

Đáp án C.

Câu 6:

15/07/2024

Cho biết $\int_{1}^{5} f (x) d x = 6, \int_{1}^{5} g (x) d x = 8$ . Tính $K = \int_{1}^{5} [4 f (x) - g (x)] d x$

Xem đáp án

Đáp án A.

Câu 7:

15/07/2024

Cho hàm số f(x) xác định trên $R \ {- 1; 1}$ thỏa mãn f'(x)= $\frac{2 x}{x^{2} - 1}$ và $f (- \sqrt{2}) = 3, f (\frac{- 1}{\sqrt{2}}) = 2$ Giá trị của biểu thức f(-2)+f( $\frac{1}{2}$ ) bằng

Xem đáp án

Đáp án C.

Câu 8:

14/07/2024

Cho $\int_{1}^{2} \frac{\sqrt{1 + x^{2}}}{x^{4}} d x = \frac{1}{c} (a \sqrt{a} - \frac{b \sqrt{b}}{b + c})$ . Tính T=a+b+c

Xem đáp án

Đáp án A.

$Đặt x = tant \Leftrightarrow \{\begin{cases} 1 + x^{2} = 1 + \tan^{2} t = \frac{1}{\cos^{2} t} \\ dx = \frac{1}{\cos^{2} t} dt \end{cases} Đổi cận : x = 1 \Rightarrow t = \frac{π}{4}; x = 2 \Rightarrow t = \arctan 2 \Rightarrow I = \int_{\frac{π}{4}}^{\arctan 2} \frac{1}{cost . {(tant)}^{2}} . \frac{1}{\cos^{2} t} dt I = \int_{\frac{π}{4}}^{\arctan 2} \cot^{4} t . \frac{1}{\cos^{3} t} dt = \int_{\frac{π}{4}}^{\arctan 2} \frac{cost}{\sin^{4} t} dt Đặt u = sint \Rightarrow du = costdt Đổi cận : t = \frac{π}{4} \Rightarrow u = \frac{\sqrt{2}}{2}; t = \arctan 2 \Rightarrow u = \frac{2 \sqrt{5}}{5} \Rightarrow I = \int_{\frac{\sqrt{2}}{2}}^{\frac{2 \sqrt{5}}{5}} \frac{du}{u^{4}} = {\frac{- 1}{3 u^{3}}}_{\frac{\sqrt{2}}{2}}^{\frac{2 \sqrt{5}}{5}} = \frac{- 5 \sqrt{5}}{24} + \frac{2 \sqrt{2}}{3} = \frac{1}{3} (2 \sqrt{2} - \frac{5 \sqrt{5}}{8}) \Rightarrow c = 3; a = 2; b = 5 \Rightarrow a + b + c = 2 + 5 + 3 = 10$

Câu 9:

22/07/2024

Ông Bình có một mảnh đất hình dạng là một phần tư elíp (hình vẽ), OA = 8m, OB = 5m. Ông đã bán với giá 100 triệu đồng trên 1 mét vuông. Hỏi ông Bình bán mảnh đất đó được bao nhiêu tiền?

Xem đáp án

Đáp án A.

Câu 10:

22/07/2024

Kí hiệu S(t) là diện tích của hình phẳng giới hạn bởi các đường y=2x+1,y=0,x=1,x=t, (t>1). Tìm t để S(t) = 10

Xem đáp án

Đáp án C.

Câu 11:

20/07/2024

Cho hàm f(x) có đạo hàm trên đoạn $[0; π], f (0) = π, \int_{0}^{π} f' (x) dx = 3 π$ . Tính $f (π)$

Xem đáp án

Đáp án C.

Câu 12:

20/07/2024

Họ nguyên hàm của hàm số f(x)= $4 x^{3} - 1$ là

Xem đáp án

Đáp án A.

$\int (4 x^{3} - 1) dx = x^{4} - x + C$

Câu 13:

21/07/2024

Cho biết $\int_{1}^{3} \frac{d x}{e^{x} - 1} = a \ln (e^{2} + e + 1) - 2 b$ với a, b là các số nguyên. Tính K=a+b

Xem đáp án

Đáp án A.

Câu 14:

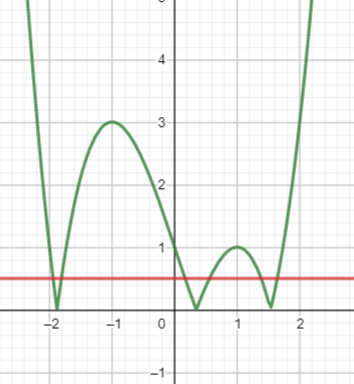
13/07/2024

Cho hàm số $y = x^{3} - 3 x + 1$ có đồ thị là hình vẽ bên. Tìm m để phương trình | $x^{3} - 3 x + 1$ | có 6 nghiệm thực phân biệt

Xem đáp án

Đáp án C.

Câu 15:

20/07/2024

Biết $\int_{1}^{e} \frac{\sqrt{1 + 3 \ln x} . \ln x}{x} d x = \frac{a}{b}$ ; trong đó a, b là 2 số nguyên dương và $\frac{a}{b}$ là phân số tối giản. Mệnh đề nào dưới đây sai ?

Xem đáp án

Đáp án B.

Câu 16:

20/07/2024

Cho hình thang cong (H) giới hạn bởi các đường $y = 3^{x}, y = 0, x = 0, x = 2$ . Đường thẳng x=t (0<t<2) chia (H) thành hai phần có diện tích S₁ và S₂ (như hình vẽ). Tìm t để S₁= 3S₂

Xem đáp án

Đáp án D.

Câu 17:

23/07/2024

Hàm số nào sau đây là một nguyên hàm của hàm số $f (x) = 2^{3 x}$

Xem đáp án

Đáp án D.

Câu 18:

17/07/2024

Cho hàm số y=f(x) liên tục trên đoạn [a;b]. Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y=f(x), trục hoành và hai đường thẳng x=a;x=b (a,b)Thể tích khối tròn xoay tạo thành khi quay D quanh trục hoành được tính theo công thức

Xem đáp án

Đáp án A.

Câu 19:

19/07/2024

Tìm nguyên hàm F(x) của hàm số $f (x) = \frac{3 + \cos 4 πx}{4}, F (4) = 2$

Xem đáp án

Đáp án B.

Câu 20:

20/07/2024

Gọi D là hình phẳng giới hạn bởi đồ thị (C) của hàm số $y = x^{4} - 2 x^{2} + 1$ tiếp tuyến D của (C) tại điểm có hoành độ x = 2 và trục hoành. Quay D xung quanh trục hoành tạo thành một khối tròn xoay có thể tích V được tính theo công thức

Xem đáp án

Đáp án A.

Câu 21:

20/07/2024

Tích phân $\int_{1}^{2} \frac{x \ln x d x}{{(x^{2} + 1)}^{2}} d x$ = aln2 + bln3 + cln5 (với a,b,c là các số hữu tỉ). Tính tổng a+b+c

Xem đáp án

Đáp án B.

Câu 22:

20/07/2024

Cho hàm số y=f(x) có đạo hàm liên tục trên [1;4], biết f(4)=3, f(1)=1 . Tính $\int_{1}^{4} 2 f' (x) d x$ .

Xem đáp án

Đáp án B.

Câu 23:

22/07/2024

Một nguyên hàm của hàm số $f (x) = 2^{x}$ là

Xem đáp án

Đáp án B.

Câu 24:

20/07/2024

Hình phẳng giới hạn bởi đồ thị hàm số y=f(x) và trục hoành gồm hai phần, phần nằm phía trên trục hoành có diện tích S₁= $\frac{8}{3}$ và phần nằm phía dưới trục hoành có diện tích S₂= $\frac{5}{12}$ (tham khảo hình vẽ bên). Tính $I = \int_{- 1}^{0} f (3 x + 1) d x$ .