Hãy chỉ ra các đường cao của tam giác HBC. Từ đó hãy chỉ ra trực tâm của tam giác đó
Với giải Bài 61 trang 83 sgk Toán 7 Tập 2 được biên soạn lời giải chi tiết sẽ giúp học sinh biết cách làm bài tập môn Toán 7. Mời các bạn đón xem:
Giải Toán 7 Luyện tập trang 83
Video giải Bài 61 trang 83 Toán lớp 7 Tập 2
Bài 61 trang 83 Toán lớp 7 Tập 2: Cho tam giác ABC không vuông. Gọi H là trực tâm của nó.
a) Hãy chỉ ra các đường cao của tam giác HBC. Từ đó hãy chỉ ra trực tâm của tam giác đó.
b) Tương tự, hãy lần lượt chỉ ra trực tâm của các tam giác HAB và HAC.
Lời giải:
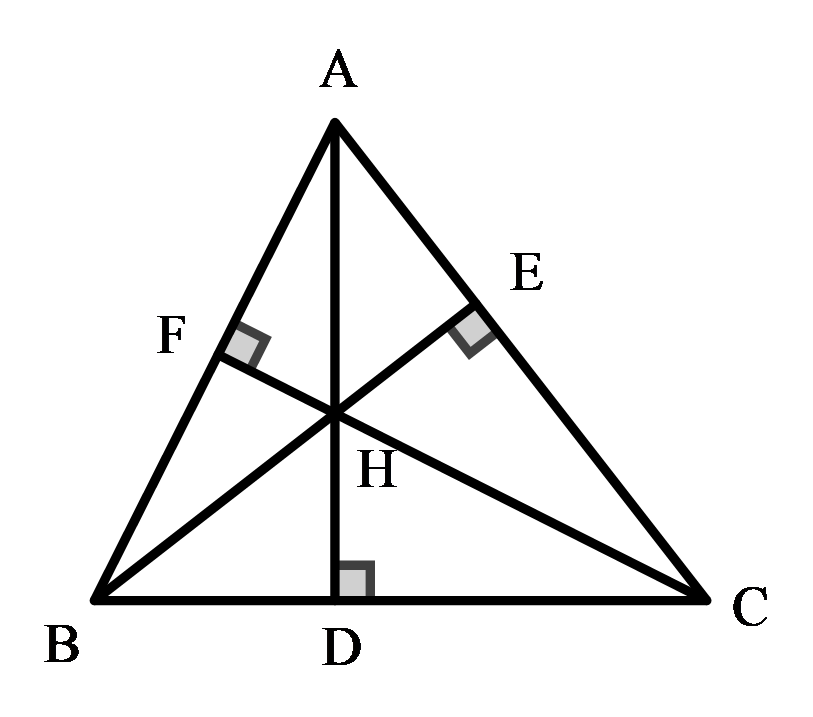
Gọi D, E, F lần lượt là chân các đường vuông góc kẻ từ A, B, C của ΔABC.
⇒ AD ⟘ BC, BE ⟘ AC, CF ⟘ AB.
H là giao điểm của ba đường cao AD, BE, CF.
a) Xét ΔHBC có :
AD ⊥ BC nên AD là đường cao từ H đến BC.
BA ⊥ HC tại F nên BA là đường cao từ B đến HC.
CA ⊥ BH tại E nên CA là đường cao từ C đến HB.
AD, BA, CA cắt nhau tại A nên A là trực tâm của ΔHCB.
b) Tương tự :
+ Trực tâm của ΔHAB là C (C là giao điểm của ba đường cao: CF, AC, BC)
+ Trực tâm của ΔHAC là B (B là giao điểm của ba đường cao: BE, AB, CB)
Xem thêm lời giải bài tập Toán lớp 7 hay, chi tiết khác:
Bài 59 trang 83 Toán 7 Tập 2: Cho hình 57. a) Chứng minh NS ⊥ LM...
Bài 60 trang 83 Toán 7 Tập 2: Trên đường thẳng d, lấy ba điểm phân biệt I, J, K (J ở giữa I và K)...
Xem thêm các chương trình khác:
