Giải SBT Tin học 10 trang 32 Cánh diều

Giải SBT Tin học 10 trang 32 Cánh diều

Câu F39 trang 32 SBT Tin 10: Đọc hiểu chương trình

Virus X có khả năng lây nhiễm mạnh, sau mỗi ngày số lượng người nhiễm tăng lên gấp đôi. Cụ thể, nếu ngày hôm nay có p người bị nhiễm thì sang ngày tiếp theo sẽ có 2p người bị nhiễm. Chương trình sau đây cho nhập vào số lượng người bị nhiễm và đưa ra sau bao nhiêu ngày thì số lượng người bị nhiễm sẽ vượt quá 1 triệu người. Em hãy hoàn thiện câu lệnh còn khuyết để nhận được chương trình đúng.

Trả lời:

Tham khảo chương trình sau:

Câu F40 trang 32 SBT Tin 10: Tìm lỗi cho cấu trúc lặp

Chương trình ở hình bên nhập vào hai số thực dương a, b với a < b và tính tổng tất cả các số nguyên không nhỏ hơn a và không lớn hơn b. Tuy nhiên, chương trình vẫn có lỗi. Chạy chương trình với a = 1,1 và b = 3,9 để thấy lỗi của chương trình. Em hãy tìm và sửa lỗi để nhận được chương trình đúng.

Trả lời:

Tham khảo chương trình sau:

Chú ý: range (m, n) dùng để khởi tạo dãy số nguyên từ m đến n - 1 (với m < n).

Câu F41 trang 32 SBT Tin 10: Tổng chữ số

Viết chương trình nhập vào số nguyên dương n và in ra tổng các chữ số trong biểu diễn thập phân của n.

Trả lời:

Thuật toán có thể áp dụng cho bài này là “tách” từng chữ số của n, với mỗi chữ số được tách ra, ta cộng dồn vào một biến S. Cụ thể là:

- Khởi tạo S = 0.

- Lặp cho đến khi n còn chữ số.

- Lấy chữ số hàng đơn vị của n, gọi là d.

- Đặt S = S + d.

- Loại bỏ chữ số hàng đơn vị của n.

Một số vấn đề kĩ thuật cần làm rõ:

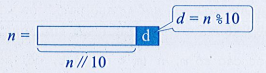
- Để lấy chữ số hàng đơn vị d của n ta có thể dùng phép tính d = n % 10.

- Để loại bỏ chữ số hàng đơn vị của n ta có thể gán n //= 10.

Với quy tắc tính như vậy, điều kiện “n còn chữ số” có thể viết thành n == 0. Bởi khi n chỉ còn một chữ số thì phép gán n = n // 10 sẽ cho n == 0.

Tham khảo chương trình sau:

Câu F42 trang 32 SBT Tin 10: Tính giai thừa

Viết chương trình nhập vào một số nguyên dương n và in ra giá trị giai thừa của n.

Trả lời:

Giai thừa của n (kí hiệu n!) là tích của các số nguyên dương từ 1 tới n. Ta cũng có thể định nghĩa quy nạp như sau:

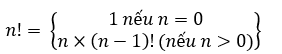
Lưu ý: 0! = 1, đây là quy ước của hàm giai thừa.

Để tính n!, ta có thể khởi tạo một biến số nguyên F = 0 ứng với giá trị 0! Sau đó với mỗi i từ 2 tới n, ta nhân F lên i lần (F= F*i). Tham khảo chương trình sau:

Câu F43 trang 32 SBT Tin 10: Tìm ước chung lớn nhất

Viết chương trình nhập vào hai số tự nhiên a, b không đồng thời bằng 0 và in ra ước số chung lớn nhất của a, b.

Trả lời:

Ước chung lớn nhất (GCD — Greatest Common Divisor) là một khái niệm quan trọng trong số học và nhiều lĩnh vực khác. Mục đích của bài toán là tìm số nguyên Z lớn nhất đồng thời là ước số của cả a và b.

Một cách tiếp cận đơn giản là khi b > 0 ta có thể thử tất cả các giá trị số nguyên d = b, b - 1, b - 2, ..., 1 và dừng lại ngay khi gặp số nguyên d là ước số của cả a và b. Còn tất nhiên khi b == 0, ước số chung lớn nhất của a và b chính là a

Phương pháp này tuy đúng nhưng có hiệu suất rất kém. Một phương pháp khác hiệu quả hơn là thuật toán Euclid (được nhà toán học người Hy Lạp đưa ra vào khoảng thế kỉ III trước công nguyên). Thuật toán Euclid như sau:

Lặp cho đến khi b ≠ 0

+ Tính r là số dư của phép chia a cho b.

+ Thay cặp số (a, b) bởi cặp số (b, r).

- Kết thúc: Giá trị a sau vòng lặp là ước chung lớn nhất của hai số ban đầu. Tham khảo chương trình sau:

Câu F44 trang 32 SBT Tin 10: Liệt kê ước số

Viết chương trình nhập vào một số nguyên dương n và in ra tất cả các ước số của n.

Trả lời:

Cách 1: Một trong những giải pháp đơn giản là thử mọi giá trị số nguyên d từ l tới n, mỗi khi gặp một giá trị ở là ước số của n thì in ra ngay giá trị d đó. Tham khảo chương trình sau:

Ví dụ:

Cách 2: Cách làm trên khá chậm khi gặp giá trị n lớn (chẳng hạn n = 10⁹). Một cải tiến nhỏ là dựa vào nhận xét: Ngoại trừ ước d = n, tất cả các ước số khác của n đều không vượt quá $\frac{n}{2}$, vì vậy ta chỉ cần thử d trong phạm vi [1, $\frac{n}{2}$] còn riêng ước d = n sẽ được in ra sau. Mặc dù tốc độ chương trình cải thiện gấp đôi, phương pháp này vẫn còn rất chậm.

Cách 3: Dựa vào nhận xét: Nếu d là ước số của n thì “$\frac{n}{d}$ cũng là ước số của n”. Trong hai ước số d và $\frac{n}{d}$, chắc chắn có một số nhỏ hơn hoặc bằng $\sqrt{n}$. Vì thế ta chỉ cần thử d trong phạm vi [1; $\sqrt{n}$], khi tìm thấy. một ước số d của n trong phạm vi này, ta in ra d và in ra luôn cả ước $\frac{n}{d}$

Lưu ý: Trường hợp d = $\frac{n}{d}$ (n là số chính phương), ta chỉ được in ra một ước để tránh trùng lặp.

Tham khảo chương trình sau: