Nội dung bài viết

    Xem thêm

    Giải các hệ phương trình sau bằng phương pháp cộng đại số: 3x + y = 3 và 2x - y = 7

    Với giải bài 20 trang 19 sgk Toán lớp 9 Tập 2 được biên soạn lời giải chi tiết sẽ giúp học sinh biết cách làm bài tập môn Toán 9. Mời các bạn đón xem:

    1 33,823 28/08/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 9 Bài 4: Giải hệ phương trình bằng phương pháp cộng đại số

    Video Giải Bài 20 trang 19 SGK Toán 9 Tập 2

    Bài 20 trang 19 SGK Toán 9 Tập 2: Giải các hệ phương trình sau bằng phương pháp cộng đại số:

    a) 3x+y=32x−y=7

    b) 2x+5y=82x−3y=0

    c) 4x+3y=62x+y=4

    d) 2x+3y=−23x−2y=−3

    e) 0,3x+0,5y=31,5x−2y=1,5

    *Phương pháp giải

    1. Nhân các vế của hai phương trình với số thích hợp sao cho các hệ số của một ẩn nào đó trong hai phương trình của hệ bằng nhau hoặc đối nhau.
    2. Sử dụng quy tắc cộng đại số để được hệ phương trình mới, trong đó có một phương trình mà hệ số của một trong hai ẩn bằng 0 (tức là phương trình một ẩn)

    *Lời giải:

    a) 3x+y=32x−y=7⇔3x+y+2x−y=3+72x−y=7

    (cộng vế với vế của hai phương trình)

    ⇔5x=102x−y=7⇔x=10:52x−y=7⇔x=22.2−y=7⇔x=2y=4−7=−3

    Vậy hệ phương trình đã cho có nghiệm (x; y) = (2; -3).

    b)2x+5y=82x−3y=0

    ⇔2x+5y−2x−3y=8−02x−3y=0 (trừ vế với vế của phương trình thứ nhất cho phương trình thứ hai)

    ⇔2x+5y−2x+3y=82x−3y=0⇔8y=82x−3y=0⇔y=8:82x−3y=0⇔2x−3.1=0y=1⇔2x−3=0y=1⇔2x=3y=1⇔x=32y=1

    Vậy hệ phương trình đã cho có nghiệm (x; y) = 32;1.

    c) 4x+3y=62x+y=4⇔4x+3y=64x+2y=8

    (nhân cả hai vế phương trình thứ hai với 2)

    ⇔4x+3y=64x+3y−4x+2y=6−8 (Trừ vế với vế của phương trình thứ nhất cho phương trình thứ hai)

    ⇔4x+3y=64x+3y−4x−2y=−2⇔4x+3y=6y=−2⇔4x+3.(−2)=6y=−2⇔4x=6+6y=−2⇔4x=12y=−2⇔x=3y=−2

    Vậy hệ phương trình đã cho có nghiệm (x; y) = (3; -2).

    d) 2x+3y=−23x−2y=−3⇔6x+9y=−66x−4y=−6

    (Ta nhân cả hai vế của phương trình một với 3 và phương trình hai với 2)

    ⇔6x+9y=−66x+9y−6x−4y=(−6)−(−6) (trừ vế với vế của phương thứ nhất cho phương trình thứ hai)

    ⇔6x+9y=−66x+9y−6x+4y=0⇔6x+9y=−613y=0⇔6x+9y=−6y=0⇔6x+9.0=−6y=0⇔6x=−6y=0⇔x=−1y=0

    Vậy hệ phương trình đã cho có nghiệm (x; y) = (-1; 0).

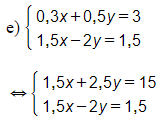
    Giải các hệ phương trình sau bằng phương pháp cộng đại số: 3x + y = 3 và 2x - y = 7 (ảnh 1)

    (Ta nhân cả hai vế của phương trình thứ nhất với 5)

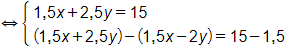
    Giải các hệ phương trình sau bằng phương pháp cộng đại số: 3x + y = 3 và 2x - y = 7 (ảnh 1)

    (trừ vế với vế của phương thứ nhất cho phương trình thứ hai)

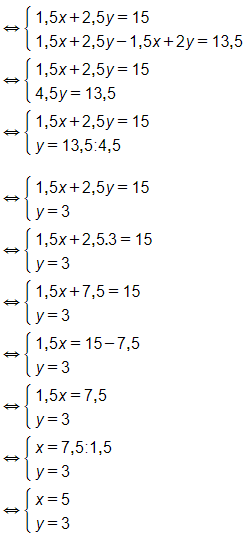
    Giải các hệ phương trình sau bằng phương pháp cộng đại số: 3x + y = 3 và 2x - y = 7 (ảnh 1)

    Vậy hệ phương trình đã cho có nghiệm (x; y) = (5; 3)

    *Cách giải hệ phương trình bằng phương pháp cộng đại số

    Bước 1: Nhân các vế của hai phương trình với số thích hợp (nếu cần) sao cho các hệ số của một ẩn nào đó trong hai phương trình của hệ bằng nhau hoặc đối nhau.

    Bước 2: Sử dụng quy tắc cộng đại số để được hệ phương trình mới, trong đó có một phương trình mà hệ số của một trong hai ẩn bằng 0 (tức là phương trình một ẩn).

    Bước 3: Giải phương trình một ẩn vừa thu được rồi suy ra nghiệm của hệ đã cho.

    Xem thêm lời giải bài tập Toán lớp 9 hay, chi tiết khác:

    Câu hỏi 1 trang 17 Toán 9 Tập 2: Áp dụng quy tắc cộng đại số để biến đổi hệ (I)...

    Câu hỏi 2 trang 17 Toán 9 Tập 2: Các hệ số của y trong hai phương trình của hệ (II) có đặc điểm gì...

    Câu hỏi 3 trang 18 Toán 9 Tập 2: a) Nêu nhận xét về các hệ số của x trong hai phương trình của hệ (III)...

    Câu hỏi 4 trang 18 Toán 9 Tập 2: Giải tiếp hệ (IV)...

    Câu hỏi 5 trang 18 Toán 9 Tập 2: Nêu một cách khác để đưa hệ phương trình (IV)...

    Bài 21 trang 19 Toán 9 Tập 2: Giải các hệ phương trình sau bằng phương pháp...

    Tham khảo các loạt bài Toán 9 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 33,823 28/08/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: