TOP 10 đề thi Học kì 2 Toán lớp 7 (Chân trời sáng tạo) năm 2025 có đáp án

Chỉ 100k mua trọn bộ Đề thi Toán 7 Chân trời sáng tạo bản word có lời giải chi tiết:

B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)

B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận tài liệu.

Xem thử tài liệu tại đây: Link tài liệu

Đề thi Học kì 2 Toán lớp 7 (Chân trời sáng tạo) năm 2025 có đáp án

BẢNG MA TRẬN ĐỀ THI HỌC KÌ 2 MÔN TOÁN LỚP 7 CHÂN TRỜI SÁNG TẠO - NĂM HỌC 2024

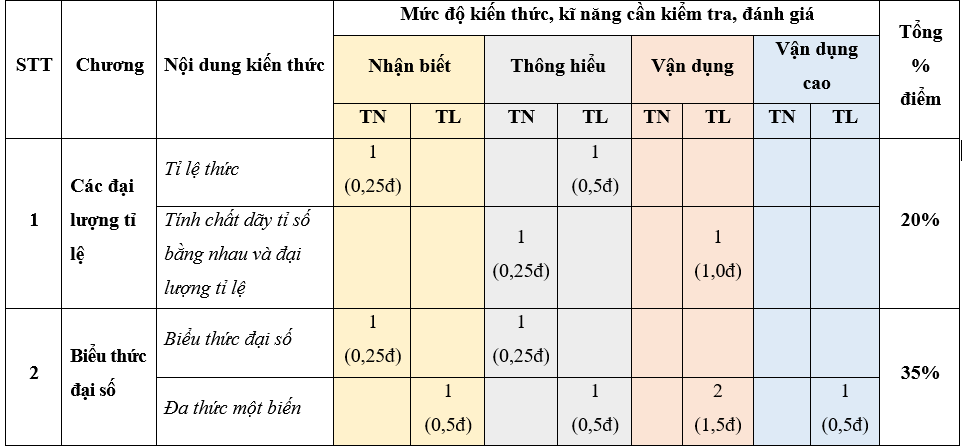
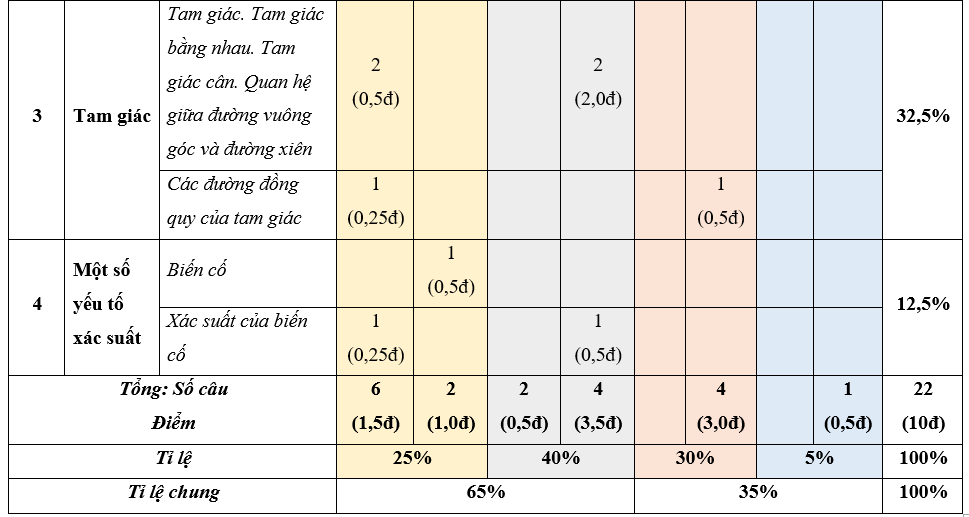
Lưu ý:

- Các câu hỏi trắc nghiệm khách quan là các câu hỏi ở mức độ nhận biết và thông hiểu, mỗi câu hỏi có 4 lựa chọn, trong đó có duy nhất 1 lựa chọn đúng.

- Các câu hỏi tự luận là các câu hỏi ở mức độ nhận biết, thông hiểu, vận dụng và vận dụng cao.

- Số điểm tính cho 1 câu trắc nghiệm là 0,25 điểm/câu; số điểm của câu tự luận được quy định trong hướng dẫn chấm nhưng phải tương ứng với tỉ lệ điểm được quy định trong ma trận.

BẢN ĐẶC TẢ MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Học kì 1

Năm học ...

Môn: Toán 7

Thời gian làm bài: 90 phút

Đề thi Học kì 1 Toán lớp 7 Chân trời sáng tạo có đáp án - (Đề số 1)

PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (2,0 điểm)

Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây:

Câu 1. Chọn khẳng định sai:

Với điều kiện các tỉ số đều có nghĩa thì

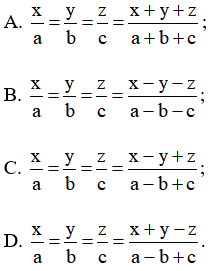
Câu 2. Cho biết y tỉ lệ thuận với x theo tỉ số k (k ≠ 0) và x tỉ lệ thuận với z theo tỉ số h (h ≠ 0). Chọn khẳng định đúng trong các khẳng định sau.

A. y và z tỉ lệ thuận với nhau theo hệ số tỉ lệ h.k;

B. y và z tỉ lệ thuận với nhau theo hệ số tỉ lệ $\frac{k}{h}$ ;

C. y và z tỉ lệ thuận với nhau theo hệ số tỉ lệ k^h;

D. y và z tỉ lệ thuận với nhau theo hệ số tỉ lệ h^k.

Câu 3. Biểu thức nào sau đây là biểu thức số?

A. 2.(3² + 4);

B. xy;

C. 5x;

D. z² + t³.

Câu 4. Mệnh đề “Tổng các lập phương của hai số a và b” được biểu thị bởi

A. a³ + b³;

B. (a + b)³;

C. a² + b²;

D. (a + b)².

Câu 5. Dựa vào hình vẽ và chọn đáp án đúng.

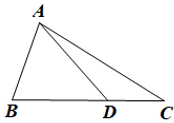
A. AB + BD > AC;

B. AD + DC > AC;

C. AB + AD > BC;

D. AB + BC < AC.

Câu 6. Cho DAMN = DDEK. Đâu là cách kí hiệu bằng nhau khác của hai tam giác trên?

A. DANM = DDEK;

B. DANM = DDKE;

C. DMAN = DEKD;

D. DMAN = DDKE.

Câu 7. Cho tam giác ABC. Ba đường trung tuyến của tam giác ABC cùng đi qua một điểm M. Khẳng định nào sau đây là đúng?

A. M cách đều ba đỉnh của tam giác ABC;

B. M cách đều ba cạnh của tam giác ABC;

C. M là trọng tâm tam giác ABC;

D. M là trực tâm tam giác ABC.

Câu 8. Một phép thử nghiệm có n kết quả và tất cả các kết quả đều có khả năng như nhau. Khi đó xác suất xảy ra của mỗi kết quả đều bằng:

A. n;

B. $\frac{1}{n}$;

C. $\frac{1}{2n}$ ;

D. $\frac{1}{n+1}$ .

PHẦN II. TỰ LUẬN (8,0 điểm)

Bài 1. (1,0 điểm) Tìm x, biết:

a) $\frac{x-1}{3}=\frac{1}{2}$ ;

b) 5x(x – 3) = (x – 2)(5x – 1) – 5.

Bài 2. (2,0 điểm) Cho hai đa thức A(x) = x – 2x² + 3x⁵ + x⁴ + x + x²;

B(x) = –2x² + x – 2 – x⁴ + 3x² – 3x⁵.

a) Thu gọn và sắp xếp hai đa thức trên theo lũy thừa giảm dần của biến.

b) Tìm đa thức M(x) sao cho B(x) = A(x) + M(x). Tìm bậc và hệ số cao nhất của đa thức M(x).

c) Tìm nghiệm của đa thức N(x) biết A(x) = N(x) – B(x).

Bài 3. (1,0 điểm) Ba phân xưởng in có tổng cộng có 47 máy in (có cùng công suất in) và mỗi phân xưởng được giao in một số trang in bằng nhau. Phân xưởng thứ nhất hoàn thành công việc trong 3 ngày, phân xưởng thứ hai trong 4 ngày và phân cưởng thứ ba trong 5 ngày. Hỏi mỗi phân xưởng có bao nhiêu máy in?

Bài 4. (1,0 điểm) Một chiếc hộp kín có chứa 5 quả bóng có kích thước và khối lượng như nhau, và được ghi lần lượt các số 5; 10; 15; 20; 25. Lấy ra ngẫu nhiên 1 quả bóng từ hộp. Xét các biến cố sau:

A: “Quả bóng lấy ra ghi số nguyên tố”;

B: “Quả bóng lấy ra ghi số chia hết cho 5”;

C: “Quả bóng lấy ra ghi số chia hết cho 6”.

D: “Quả bóng lấy ra ghi số tròn chục”.

a) Trong các biến cố trên, chỉ ra biến cố nào là chắc chắn, không thể.

b) Tính xác suất của các biến cố A và D.

Bài 5. (2,5 điểm) Cho tam giác ABC vuông tại A (AB < AC). Trên cạnh BC lấy điểm D sao cho BD = BA. Đường thẳng vuông góc với BC tại D cắt cạnh AC tại M, cắt tia BA tại N.

a) So sánh các góc của tam giác ABC.

b) Chứng minh DABM = DDBM. Từ đó suy ra MA = MD.

c) Tam giác MNC là tam giác gì? Tại sao?

d) Gọi I là trung điểm của CN. Chứng minh ba điểm B, M, I thẳng hàng.

Bài 6. (0,5 điểm) Tìm giá trị nguyên dương của x để đa thức x³ – 3x² – 3x – 1 chia hết cho đa thức x² + x + 1.

ĐÁP ÁN ĐỀ SỐ 01

PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (2,0 điểm)

Bảng đáp án:

Hướng dẫn giải phần trắc nghiệm

Câu 1.

Đáp án đúng là: D

Ta có $\frac{x}{a}=\frac{y}{b}=\frac{z}{c}=\frac{x+y-z}{a+b-c}\ne \frac{x+y-z}{a-b+c}$ nên D sai.

Câu 2.

Đáp án đúng là: A

Vì y tỉ lệ thuận với x theo tỉ số k (k ≠ 0) nên ta có y = kx;

x tỉ lệ thuận với z theo tỉ số h (h ≠ 0) nên ta có x = hz.

Khi đó ta có y = kx = k.(hz) = (kh).z nên y và z tỉ lệ thuận với nhau theo hệ số tỉ lệ k.h.

Câu 3.

Đáp án đúng là: A

Biểu thức số là: 2.(3² + 4).

Câu 4.

Đáp án đúng là: A

Tổng các lập phương của hai số a và b là a³ + b³.

Câu 5.

Đáp án đúng là: B

Vì trong một tam giác tổng độ dài hai cạnh bất kì lớn hơn độ dài cạnh còn lại.

Nên với tam giác ADC có AD + DC > AC.

Câu 6.

Đáp án đúng là: B

Vì DAMN = DDEK nên $\left\{\begin{array}{l}\hat{A}=\hat{D}; \hat{M}=\hat{E}; \hat{N}=\hat{K}\\ AM=DE; MN=EK; AN=DK\end{array}\right.$

Vậy một trong những cách kí hiệu bằng nhau khác của hai tam giác trên là:

DANM = DDKE.

Câu 7.

Đáp án đúng là: C

Ba đường trung tuyến của tam giác ABC cùng đi qua một điểm M, điểm M này gọi là trọng tâm của tam giác ABC.

Câu 8.

Đáp án đúng là: B

Khi tất cả các kết quả của một trò chơi hay phép thử nghiệm ngẫu nhiên đều có khả năng xảy ra bằng nhau thì xác suất xảy ra của mỗi kết quả đều là $\frac{1}{n}$ , trong đó n là số các kết quả.

PHẦN II. TỰ LUẬN (8,0 điểm)

Hướng dẫn giải phần tự luận

Bài 1. (1,0 điểm)

a)

$\frac{x-1}{3}=\frac{1}{2}$

2.(x – 1) = 3.1

2x – 2 = 3

2x = 5

$x=\frac{5}{2}$

Vậy $x=\frac{5}{2}$

b) 5x(x – 3) = (x – 2)(5x – 1) – 5

5x² – 15x = 5x² – x – 10x + 2 – 5

–4x = –3

x=$\frac{3}{4}$

Vậy $x = \frac{3}{4}$

Bài 2. (2,0 điểm)

a) A(x) = x – 2x² + 3x⁵ + x⁴ + x + x²

= 3x⁵ + x⁴ – x² + 2x.

B(x) = –2x² + x – 2 – x⁴ + 3x² – 3x⁵

= – 3x⁵ – x⁴ + x² + x – 2

b) B(x) = A(x) + M(x)

Suy ra M(x) = B(x) – A(x)

M(x) = (– 3x⁵ – x⁴ + x² + x – 2) – (3x⁵ + x⁴ – x² + 2x)

= – 3x⁵ – x⁴ + x² + x – 2 – 3x⁵ – x⁴ + x² – 2x

= –6x⁵ – 2x⁴ + 2x² – x – 2.

Đa thức M(x) có bậc là 5, hệ số cao nhất là –6.

c) A(x) = N(x) – B(x)

Suy ra N(x) = A(x) + B(x)

N(x) = (3x⁵ + x⁴ – x² + 2x) + (– 3x⁵ – x⁴ + x² + x – 2)

= 3x⁵ + x⁴ – x² + 2x – 3x⁵ – x⁴ + x² + x – 2

= – x – 2.

N(x) = 0

Suy ra – x – 2 nên x = – 2.

Vậy đa thức N(x) có nghiệm là x = – 2.

Bài 3. (1,0 điểm)

Gọi x, y, z lần lượt là số máy in của các phân xưởng thứ nhất, thứ hai, thứ ba.

Tổng số máy của ba phân xưởng là x + y + z = 47.

Vì số ngày hoàn thành công việc tỉ lệ nghịch với số máy nên ta có:

3x = 4y = 5z hay $\frac{{\displaystyle \frac{x}{1}}}{3}=\frac{{\displaystyle \frac{y}{1}}}{4}=\frac{{\displaystyle \frac{z}{1}}}{5}$ .

Theo tính chất của dãy tỉ số bằng nhau, ta có:

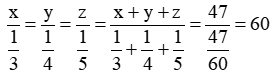
Suy ra $x=60.\frac{1}{3}=20; y=60.\frac{1}{4}=15; z=60.\frac{1}{5}=12$

Vậy số máy in của ba phân xưởng lần lượt là 20; 15; 12 (máy in).

Bài 4. (1,0 điểm)

a) Biến cố B là biến cố chắc chắn, biến cố C là biến cố không thể.

b) Vì 5 quả bóng có kích thước và khối lượng như nhau nên mỗi quả bóng đều có cùng khả năng được chọn.

• Trong 5 quả bóng ghi lần lượt các số 5; 10; 15; 20; 25, chỉ có 1 quả bóng ghi số nguyên tố là 5. Do đó xác xuất của biến cố A là $P\left(A\right)=\frac{1}{5}$ .

• Trong 5 quả bóng ghi lần lượt các số 5; 10; 15; 20; 25, có 2 quả bóng ghi số tròn chục là 10; 20. Do đó xác xuất của biến cố D là $P\left(A\right)=\frac{2}{5}$ .

Bài 5. (2,5 điểm)

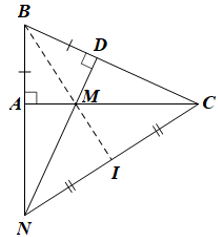
a) Tam giác ABC là tam giác vuông tại A nên cạnh huyền BC là cạnh lớn nhất.

Mà AB < AC nên AB < AC < BC.

Suy ra (quan hệ giữa góc và cạnh đối diện trong tam giác).

b) Xét DABM và DDBM có:

$\widehat{BAM}=\widehat{BDM}$ = 90⁰;

BA = BD (giả thiết);

BM là cạnh chung

Do đó DABM = DDBM (cạnh huyền – cạnh góc vuông)

Suy ra MA = MD (hai cạnh tương ứng).

c) Xét DANM và DDCM có:

$\widehat{NAM}=\widehat{CDM}=90°$;

MA = MD (chứng minh câu b);

$\widehat{AMN}=\widehat{DMC}$(hai góc đối đỉnh).

Do đó DANM = DDCM (cạnh góc vuông – góc nhọn kề)

Suy ra MN = MC (hai cạnh tương ứng).

Tam giác MNC có MN = MC nên là tam giác cân tại M.

d) Do DMNC cân tại M có I là trung điểm của NC nên MI là đường trung tuyến của DMNC.

Khi đó MI đồng thời là đường cao của DMNC hay MI ⊥ NC (1)

Xét DBNC có hai đường cao CA, ND cắt nhau tại M nên M là trực tâm của DBNC.

Suy ra BM ⊥ NC (2)

Từ (1) và (2) suy ra ba điểm B, M, I thẳng hàng.

Bài 6. (0,5 điểm)

Thực hiện phép chia đa thức như sau:

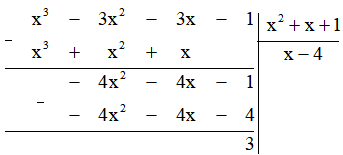
Để đa thức x³ – 3x² – 3x – 1 chia hết cho đa thức x² + x + 1 thì 3 ⋮ (x² + x + 1).

Tức là x² + x + 1 ∈ Ư(3) = {–3; 3; –1; 1}.

Do x > 0 nên x² + x + 1 > 1

Do đó x² + x + 1 = 3

x² + x – 2 = 0

x² – x + 2x – 2 = 0

x(x – 1) + 2(x – 1) = 0

(x – 1)(x + 2) = 0

Suy ra x = 1 (thỏa mãn) hoặc x = – 2 (loại).

Vậy x = 1 thì đa thức x³ – 3x² – 3x – 1 chia hết cho đa thức x² + x + 1.

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Học kì 2

Năm học ...

Môn: Toán 7

Thời gian làm bài: 90 phút

Đề thi Học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - (Đề số 2)

PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (2,0 điểm)

Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây:

Câu 1. Chọn câu đúng. Với điều kiện các tỉ số đều có nghĩa thì từ $\frac{x}{y}=\frac{u}{v}$ ta có

A. $\frac{x}{y}=\frac{x+u}{y+v}$ ;

B. $\frac{x}{y}=\frac{x+u}{y-v}$ ;

C. $\frac{x}{y}=\frac{x-u}{y+v}$ ;

D. $\frac{x}{y}=\frac{x-u}{y.v}$.

Câu 2. Giả sử x và y là hai đại lượng tỉ lệ thuận, x₁; x₂ là hai giá trị khác nhau của x và y₁; y₂ là hai giá trị tương ứng của y. Biết y₁ – x₁ = 7 và x₂ = – 4; y₂ = 3, giá trị của x₁; y₁ là

A. x₁ = –28; y₁ = 21;

B. x₁ = –3; y₁ = 4;

C. x₁ = –4; y₁ = 3;

D. x₁ = 4; y₁ = –3.

Câu 3. Cho a, b là các số đã biết không thay đổi giá trị. Các biến trong biểu thức đại số ax + by là

A. a; b;

B. a; b; x; y;

C. x; y;

D. a; x.

Câu 4. Giá trị của biểu thức x + 2x²y – y² tại x = –1 và y = –1 là

A. 0;

B. –4;

C. 2;

D. –2.

Câu 5. Chọn khẳng định đúng.

Xét tam giác ABC có:

A. AB + BC < AC;

B. AC – BC > AB;

C. AB + BC > AC;

D. AB + BC = AC.

Câu 6. Cho tam giác ABC có AH ⊥ BC (H ∈ BC) thì

A. AB > AH;

B. BH = CH;

C. AB < AC;

D. AH < BC.

Câu 7. Cho tam giác ABC với hai đường trung tuyến BM và CN cắt nhau tại G. Kết luận nào sau đây là sai?

A. CG = $\frac{2}{3}CN$;

B. $GN=\frac{1}{2}GC$ ;

C. $GM=\frac{2}{3}BM$ ;

D. GB = 2GM.

Câu 8. Khẳng định nào sau đây là không đúng?

A. Biến cố chắc chắn luôn xảy ra;

B. Biến cố không thể không bao giờ xảy ra;

C. Xác suất của biến cố ngẫu nhiên bằng 1;

D. Biến cố có khả năng xảy ra cao hơn sẽ có xác suất lớn hơn.

PHẦN II. TỰ LUẬN (8,0 điểm)

Bài 1. (1,0 điểm) Tìm x, biết:

a) $\frac{3}{x}=\frac{x}{27}$ ;

b) (2x + 3)(x + 2) = (x – 4)(2x + 1)

Bài 2. (2,0 điểm) Cho hai đa thức P(x) = 6x⁵ + 15 – 7x – 4x² – x⁵;

Q(x) = –5x⁵ – 2x + 4x² + 5x – 7.

a) Thu gọn và sắp xếp hai đa thức trên theo lũy thừa giảm dần của biến.

b) Tìm bậc và hệ số tự do của đa thức K(x) biết K(x) = P(x) – Q(x).

c) Tìm nghiệm của đa thức M(x) biết M(x) = P(x) + Q(x).

Bài 3. (1,0 điểm) Số đo ba góc của một tam giác tỉ lệ với 4; 6; 8. Tính số đo mỗi góc của tam giác đó.

Bài 4. (1,0 điểm) Gieo ngẫu nhiên xúc xắc 6 mặt cân đối một lần. Xét các biến cố sau:

A: “Số chấm xuất hiện trên con xúc xắc là số lẻ và chia hết cho 3”.

B: “Số chấm xuất hiện trên con xúc xắc là số có một chữ số”.

C: “Số chấm xuất hiện trên con xúc xắc là số tròn trăm”.

D: “Số chấm xuất hiện trên con xúc xắc là số chia cho 4 dư 1”.

a) Trong các biến cố trên, hãy chỉ ra biến cố nào là biến cố chắc chắn, biến cố nào là biến cố không thể.

b) Tính xác suất của biến cố ngẫu nhiên có trong các biến cố A, B, C, D.

Bài 5. (2,5 điểm) Cho ∆ABC cân tại A có .

a) Tính số đo các góc của tam giác ABC từ đó so sánh các cạnh của tam giác ABC.

b) Đường trung trực của cạnh AC cắt AB tại D. Trên cạnh AC lấy điểm E sao cho CE = BD. Chứng minh ∆BCD = ∆CBE. Từ đó suy ra $\widehat{BDC}=\widehat{CEB}$ .

c) Kẻ đường trung tuyến AM của tam giác ABC. Chứng minh ba đường thẳng AM, BE, CD đồng quy tại một điểm.

Bài 6. (0,5 điểm) Tìm số nguyên x để đa thức A(x) = 2x³ – 3x² + 2x + 2 chia hết cho đa thức B(x) = x² + 1.

ĐÁP ÁN ĐỀ SỐ 02

PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (2,0 điểm)

Bảng đáp án:

Hướng dẫn giải phần trắc nghiệm

Câu 1.

Đáp án đúng là: A

Theo tính chất của dãy tỉ số bằng nhau ta có: $\frac{x}{y}=\frac{u}{v}=\frac{x+u}{y+v}=\frac{x-u}{y-v}$ nên A đúng.

Câu 2.

Đáp án đúng là: C

Áp dụng tính chất tỉ lệ thuận và tính chất dãy tỉ số bằng nhau

Vì x và y là hai đại lượng tỉ lệ thuận nên $\frac{x_1}{x_2}=\frac{y_1}{y_2}$

Suy ra $\frac{x_1}{-4}=\frac{y_1}{3}=\frac{y_1-x_2}{3-(-4)}=\frac{7}{7}=1$

Nên x₁ = 1.(–4) = –4; y₁ = 1.3 = 3.

Câu 3.

Đáp án đúng là: C

Các biến trong biểu thức đại số ax + by là x; y.

Câu 4.

Đáp án đúng là: B

Thay x = –1 và y = –1 vào biểu thức đã cho ta được: –1 + 2.(–1)².(–1) – (–1)² = –4.

Câu 5.

Đáp án đúng là: C

Theo bất đẳng thức trong tam giác ta có AB + BC > AC.

Câu 6.

Đáp án đúng là: A

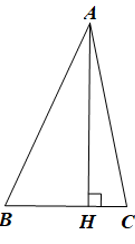
AB, AH lần lượt là đường xiên, đường vuông góc kẻ từ A đến BC. Do đó AB > AH.

Câu 7.

Đáp án đúng là: C

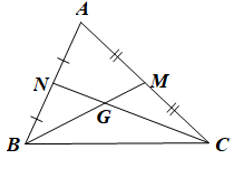
Cho DABC có hai đường trung tuyến BM và CN cắt nhau tại G nên G là trọng tâm của DABC.

Khi đó $CG=\frac{2}{3}CN$; $GN=\frac{1}{2}GC; GM=\frac{1}{3}BM; GB=2GM$. Do đó C sai.

Câu 8.

Đáp án đúng là: C

Biến cố ngẫu nhiên A có xác suất như sau: 0 < P(A) < 1.

PHẦN II. TỰ LUẬN (8,0 điểm)

Hướng dẫn giải phần tự luận

Bài 1. (1,0 điểm)

a) $\frac{3}{x}=\frac{x}{27}$

x² = 81

x = 9 hoặc x = –9.

Vậy x ∈ {9; –9}.

b) (2x + 3)(x + 2) = (x – 4)(2x + 1)

2x² + 4x + 3x + 6 = 2x² + x – 8x – 4

14x = –10

x = $-\frac{5}{7}$

Vậy x = $-\frac{5}{7}$.

Bài 2. (2,0 điểm)

a) P(x) = 6x⁵ + 15 – 7x – 4x² – x⁵

= 5x⁵ – 4x² – 7x + 15.

Q(x) = –5x⁵ – 2x + 4x² + 5x – 7

= –5x⁵ + 4x² + 3x – 7.

b) K(x) = P(x) – Q(x)

K(x) = (5x⁵ – 4x² – 7x + 15) – (–5x⁵ + 4x² + 3x – 7)

= 5x⁵ – 4x² – 7x + 15 + 5x⁵ – 4x² – 3x + 7

= 10x⁵ – 8x² – 10x + 22.

Đa thức K(x) có bậc là 5, hệ số cao nhất là 10.

c) M(x) = P(x) + Q(x).

M(x) = (5x⁵ – 4x² – 7x + 15) + (–5x⁵ + 4x² + 3x – 7)

= 5x⁵ – 4x² – 7x + 15 – 5x⁵ + 4x² + 3x – 7

= –4x + 8.

Ta có M(x) = 0

Suy ra –4x + 8 = 0

x = 2.

Vậy đa thức M(x) có nghiệm là x = 2.

Bài 3. (1,0 điểm)

Gọi số đo ba góc của tam giác đó lần lượt là x, y, z (0° < x, y, z < 180°).

Tổng số đo ba góc trong tam giác bằng 180° nên x + y + z = 180°.

Số đo ba góc của một tam giác tỉ lệ với 4; 6; 8 nên $\frac{x}{4}=\frac{y}{6}=\frac{z}{8}$ .

Theo tính chất dãy tỉ số bằng nhau ta có:

Suy ra x = 4.10° = 40°; y = 6.10° = 60°; z = 8.10° = 80°.

Vậy số đo ba góc của một tam giác là 40°; 60° và 80°.

Bài 4. (1,0 điểm)

a) Biến cố B là biến cố chắc chắn, biến cố C là biến cố không thể.

b) Biến cố ngẫu nhiên là biến cố A và D.

Khi gieo ngẫu nhiên xúc xắc 6 mặt cân đối thì có 6 kết quả xảy ra đối với mặt xuất hiện của con xúc xắc và 6 kết quả này có khả năng xảy ra như nhau.

Trong các số 1; 2; 3; 4; 5; 6, chỉ có 1 số lẻ và chia hết cho 3 là số 3. Vậy xác suất của biến cố A là $\frac{1}{6}$ .

Trong các số 1; 2; 3; 4; 5; 6, có 2 số chia cho 4 dư 1 là số 1; 5. Vậy xác suất của biến cố D là $\frac{2}{6}=\frac{1}{3}$ .

Bài 5. (2,5 điểm)

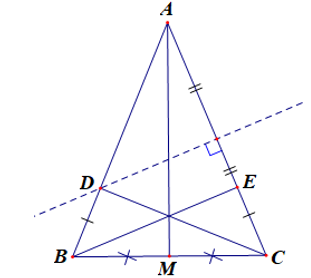
a) Tam giác ABC cân tại A nên AB = AC và $\hat{B}=\hat{C}$ .

Theo định lí tổng ba góc của một tam giác ta có: $\hat{A}+\hat{B}+\hat{C}=180°$ .

Suy ra 2$\hat{B}$=$180°-\hat{A}=180°-45°=135°$.

Do đó $\hat{B}=\hat{C}=67,5°$ .

Vì $\hat{A}<\hat{B}$ nên BC < AC (quan hệ giữa góc và cạnh trong tam giác).

Vậy BC < AB = AC.

b) Xét ∆BCD và ∆CBE, có:

BC là cạnh chung.

CE = BD (giả thiết).

$\widehat{DBC}=\widehat{ECB}$ (do ∆ABC cân tại A).

Do đó ∆BCD = ∆CBE (c.g.c)

Suy ra $\widehat{BDC}=\widehat{CEB}$ (hai góc tương ứng).

c) Vì điểm D thuộc đường trung trực của cạnh AC nên DA = DC.

Do đó ∆ACD cân tại D.

Suy ra $\widehat{ACD}=\widehat{CAD}=45°$ (tính chất tam giác cân)

∆ACD cân tại D có nên ∆ACD vuông cân tại D.

Suy ra CD ⊥ AB hay $\widehat{BDC}=90°$

Mà $\widehat{BDC}=\widehat{CEB}$ (câu b) nên $\widehat{CEB}=90°$ hay BE ⊥ AC.

Vì ∆ABC cân tại A có AM là đường trung tuyến nên M là trung điểm BC.

Xét ∆ABM và ∆ACM, có:

AM là cạnh chung,

AB = AC (do ∆ABC cân tại A),

BM = CM (do M là trung điểm BC).

Do đó ∆ABM = ∆ACM (c.c.c).

Suy ra $\widehat{AMB} =\widehat{AMC}$ (cặp góc tương ứng).

Mà $\widehat{AMB}+\widehat{AMC}=180°$ (hai góc kề bù).

Suy ra $\widehat{AMB}=\widehat{AMC}=180°:2=90°$ .

Do đó AM ⊥ BC.

Vì vậy AM là đường cao của ∆ABC.

∆ABC có AM, BE, CD là ba đường cao, suy ra AM, BE, CD đồng quy tại một điểm, điểm đó là trực tâm của ∆ABC.

Bài 6. (0,5 điểm)

Ta thực hiện đặt tính chia đa thức như sau:

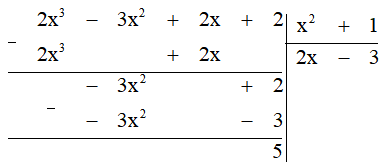
Để đa thức A(x) = 2x³ – 3x² + 2x + 2 chia hết cho đa thức B(x) = x² + 1 thì 5 ⁝ (x² + 1)

Hay (x² + 1) ∈ Ư(5) = {–1; 1; –5; 5}.

Mà x² + 1 ≥ 1 với mọi số nguyên x.

Do đó (x² + 1) ∈ {1; 5}.

• Với x² + 1 = 1 suy ra x = 0 (thỏa mãn x là số nguyên)

• Với x² + 1 = 5

Suy ra x² = 4

Do đó x = 2 (thỏa mãn) hoặc x = –2 (thỏa mãn)

Vậy có 3 giá trị của x thỏa mãn đề bài là x ∈ {0; –2; 2}.

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Học kì 2

Năm học ...

Môn: Toán 7

Thời gian làm bài: 90 phút

Đề thi Học kì 2 Toán lớp 7 Chân trời sáng tạo - (Đề số 3)

PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (2,0 điểm)

Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây:

Câu 1. Biết x, y là hai đại lượng tỉ lệ nghịch và khi x = 3 thì y = –15 . Hệ số tỉ lệ nghịch của y đối với x là:

A. –5;

B. –45;

C. 45;

D. 5.

Câu 2. Cho $\frac{x}{3}=\frac{y}{-2}$ và x – y = 10, khi đó:

A. x = –6; y = 4;

B. x = 30; y = –20;

C. x = –30; y = 20;

D. x = 6; y = –4.

Câu 3. Tích của hai đơn thức xy và 3x² bằng

A. 3x³;

B. 3x³y;

C. 3xy²;

D. 3x²y.

Câu 4. Giá trị của biểu thức A = x² – y² + z² tại x = –1, y = 1 và z = –1 là

A. –1;

B. 1;

B. –2;

D. 3.

Câu 5. Trong các bộ ba độ dài đoạn thẳng dưới đây, bộ ba nào có thể là độ dài ba cạnh của một tam giác?

A. 7 cm; 9 cm; 18 cm;

B. 2 cm; 5 cm; 7 cm;

C. 1 cm; 7 cm; 9 cm;

D. 6 cm; 11 cm; 13 cm.

Câu 6. Cho tam giác DEF có $\hat{D}$ = $38°$và $\hat{E}=110°$. Độ dài các cạnh của ∆DEF sắp xếp theo thứ tự tăng dần là

A. DE; EF; DF;

B. DE; DF; EF;

C. EF; DE; DF;

D. EF; DF; DE.

Câu 7. Trong một tam giác, tâm của đường tròn tiếp xúc ba cạnh của tam giác là

A. giao điểm của ba đường trung tuyến.

B. giao điểm của ba đường trung trực.

C. giao điểm của ba đường phân giác.

D. giao điểm của ba đường cao.

Câu 8. Một chuồng thỏ nhốt 10 con thỏ trắng và 8 thỏ xám, lấy ngẫu nhiên 4 con thỏ từ chuồng thỏ trên, biến cố nào sau đây có thể xảy ra?

A. “Lấy được 3 thỏ trắng và 2 thỏ xám”.

B. “Lấy được 4 thỏ trắng và 1 thỏ xám”.

C. “Lấy được nhiều nhất 4 thỏ xám”.

D. “Lấy được ít nhất 5 thỏ trắng”.

PHẦN II. TỰ LUẬN (8,0 điểm)

Bài 1. (1,0 điểm) Tìm x, biết:

a) $\frac{-2{\displaystyle \frac{1}{10}}}{2{\displaystyle \frac{1}{15}}}=\frac{x-1}{-4}$ ; b) 2x(3x – 1) - 6x(x + 2) = 42.

Bài 2. (2,0 điểm) Cho hai đa thức: A(x) = x⁴ + 5x³ – 6x + 2x² + 10x – 5x³ + 1;

B(x) = x⁴ – 2x³ + 2x² + 6x³ + 1.

a) Thu gọn và sắp xếp hai đa thức trên theo lũy thừa giảm dần của biến.

b) Tìm đa thức M(x) sao cho A(x) = B(x) + M(x).

c) Tìm nghiệm của đa thức M(x).

Bài 3. (1,0 điểm) Trong buổi trồng cây gây rừng, mỗi học sinh lớp 7A trồng được 12 cây, mỗi học sinh lớp 7B trồng được 14 cây. Hỏi mỗi lớp có bao nhiêu học sinh tham gia trồng cây? Biết rằng cả hai lớp có 78 học sinh tham gia trông cây và số cây trồng được của hai lớp bằng nhau.

Bài 4. (1,0 điểm) Bạn Mai có một hộp bút đựng hai chiếc bút màu xanh và 1 chiếc bít màu đỏ. Bạn Mai lấy ngẫu nhiên một chiếc bút từ hợp cho bạn Huy mượn. Xét các biến cố sau:

A: “Mai lấy được chiếc bút màu đỏ”;

B: “Mai lấy được chiếc bút màu xanh”.

C: “Mai lấy được chiếc bút màu đen”.

D. “Mai lấy được chiếc bút màu đỏ hoặc màu xanh”.

a) Trong các biến cố trên, hãy chỉ ra biến cố không thể, biến cố chắc chắn.

b) Tính xác suất của biến cố ngẫu nhiên có trong các biến cố trên.

Bài 5. (2,5 điểm) Cho tam giác ABC vuông tại A, đường trung tuyến CM. Trên tia đối của tia MC lấy điểm D sao cho MD = MC.

a) Chứng minh rằng DMAC = D MBD.

b) Chứng minh rằng AC + BC > 2CM.

c) Gọi K là điểm trên đoạn thẳng AM sao cho $AK=\frac{2}{3}AM$ . Gọi N là giao điểm của CK và AD, I là giao điểm của BN và CD. Chứng minh rằng CD = 3ID.

Bài 6. (0,5 điểm) Tìm số nguyên x để đa thức A(x) = 8x² – 4x + 1 chia hết cho đa thức B(x) = 2x + 1.

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Học kì 2

Năm học 2022 - 2023

Môn: Toán 7

Thời gian làm bài: 90 phút

Đề thi Học kì 2 Toán lớp 7 Chân trời sáng tạo - (Đề số 4)

Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây:

Câu 1. Nếu y tỉ lệ thuận với x theo hệ số tỉ lệ là k (k ≠ 0) thì x tỉ lệ thuận với y theo hệ số tỉ lệ là:

A. k;

B. –k;

C. $\frac{1}{k}$ ;

D.$-\frac{1}{k}$ .

Câu 2. Cho hai số x, y thỏa mãn $\frac{x}{3}=\frac{y}{8}$ và x + y = –22. Khi đó x – y bằng

A. –10;

B. –11;

C. 10;

D. 11.

Câu 3. Biến số trong biểu thức đại số sau “3x² – xyz + 2z²” là

A. x; y;

B. x²; xyz; z².

C. x; y; z;

D. x; z.

Câu 4. Giá trị của biểu thức A = xy – yz + xz tại x = –1; y = 1 và z = –1 là

A. –1;

B. 1;

C. –2;

D. 2.

Câu 5. Cho tam giác ABC có AB = 1 cm, BC = 4 cm. Biết độ dài cạnh AC là số nguyên, độ dài cạnh AC là

A. 1 cm;

B. 2 cm;

C. 4 cm;

D. 5 cm.

Câu 6. Cho DABC biết $\hat{A}=40°; \hat{B}=50°$. Tam giác ABC là tam giác gì?

A. Tam giác nhọn;

B. Tam giác vuông;

C. Tam giác cân;

D. Tam giác tù.

Câu 7. Trong một tam giác, tâm của đường tròn đi qua ba đỉnh của tam giác là

A. giao điểm của ba đường trung tuyến.

B. giao điểm của ba đường trung trực.

C. giao điểm của ba đường phân giác.

D. giao điểm của ba đường cao.

Câu 8. Lấy ngẫu nhiên một quả bóng từ một hộp gồm 10 quả bóng trong đó có 2 quả bóng màu xanh, 3 quả bóng màu vàng và 5 quả bóng màu trắng. Biến cố nawof sau đây có xác suất cao nhất?

A. Lấy được quả bóng màu xanh;

B. Lấy được quả bóng màu vàng;

C. Lấy được quả bóng màu trắng;

D. Lấy được quả bóng màu xanh hoặc trắng hoặc vàng.

PHẦN II. TỰ LUẬN (8,0 điểm)

Bài 1. (1,0 điểm)

a) $\frac{x-1}{3}=\frac{5}{7}$ ; b) 2x(12x – 5) – 8x(3x – 1) = 30.

Bài 2. (2,0 điểm) Cho hai đa thức: M(x) = 3x³ – 2x + 4x² – x + 5;

N(x) = 2x² – x + 3x³ – 3x² + 9.

a) Thu gọn và sắp xếp hai đa thức trên theo lũy thừa giảm dần của biến.

b) Tìm đa thức A(x) sao cho A(x) = M(x) + N(x).

c) Biết A(x) – B(x) = 6x³ + 3x² + 2x. Tìm nghiệm của đa thức B(x).

Bài 3. (1,0 điểm) Đồng bạch là một loại hợp kim của nikel, zinc (kẽm) và copper (đồng). Khối lượng của nikel, zinc và copper lần lượt tỉ lệ thuận với 3; 4 và 13. Hỏi cần bao nhieu kilôgam nikel, zinc và copper để sản xuất 70 kg đồng bạch?

Bài 4. (1,0 điểm) Một ngân hàng đề thi gồm 100 câu hỏi trong đó có 20 câu hỏi khó, 50 câu hỏi trung bình và 30 câu hỏi dễ. Học sinh sẽ bốc thăm ngẫu nhiên 1 câu hỏi để trả lời. Xét các biến cố:

A: “Bốc được câu hỏi khó”;

B: “Bốc được câu hỏi trung bình”;

C: “Bốc được câu hỏi dễ”;

D: “Không bốc được câu hỏi khó”.

a) Sắp xếp các xác xuất P(A), P(B), P(C) theo thứ tự giảm dần.

b) Biến cố D có là biến cố ngẫu nhiên không? Nếu có hãy chỉ ra trường hợp để D xảy ra, D không xảy ra.

Bài 5. (2,5 điểm) Cho tam giác ABC cân tại A có BC = 6 cm. Kẻ AH ⊥ BC tại H.

a) Chứng minh ∆AHB = DAHC, từ đó suy ra H là trung điểm của BC.

b) Trên tia AB lấy điểm E sao cho AB = BE. Gọi I là trung điểm của EC, BC cắt AI tại M. Chứng minh 2BH = 3BM và tính độ dài BM.

c) Chứng minh AB + AC > 6HM.

Bài 6. (0,5 điểm) Cho đa thức:

A(x) = x²³ – 2023x²² + 2023x²¹ – 2023x²⁰ + 2023x¹⁹ + … – 2023x² + 2023x – 1.

Tính giá trị của đa thức A(x) tại x = 2022.

Để xem trọn bộ Đề thi Toán 7 Chân trời sáng tạo có đáp án, Thầy/ cô vui lòng Tải xuống!

Xem thêm đề thi các môn lớp 7 bộ sách Chân trời sáng tạo hay, có đáp án chi tiết:

Đề thi Học kì 2 Tin học lớp 7 Chân trời sáng tạo (10 đề có đáp án + ma trận)

Đề thi Học kì 2 Văn lớp 7 Chân trời sáng tạo (10 đề có đáp án + ma trận)

Đề thi Học kì 2 Tiếng Anh lớp 7 Friends plus (10 đề có đáp án + ma trận) | Chân trời sáng tạo

Đề thi Học kì 2 Khoa học tự nhiên lớp 7 Chân trời sáng tạo (10 đề có đáp án + ma trận)

Đề thi Học kì 2 Lịch sử và Địa lí lớp 7 Chân trời sáng tạo (10 đề có đáp án + ma trận)

Đề thi Học kì 2 Giáo dục công dân lớp 7 Chân trời sáng tạo (10 đề có đáp án + ma trận)

Đề thi Học kì 2 Công nghệ lớp 7 Chân trời sáng tạo (10 đề có đáp án + ma trận)