TOP 10 đề thi Giữa Học kì 2 (Chân trời sáng tạo) năm 2025 có đáp án

Chỉ 100k mua trọn bộ Đề thi Toán 7 Chân trời sáng tạo bản word có lời giải chi tiết:

B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)

B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận tài liệu.

Xem thử tài liệu tại đây: Link tài liệu

Đề thi Giữa Học kì 2 Toán lớp 7 (Chân trời sáng tạo) năm 2025 có đáp án

BẢNG MA TRẬN ĐỀ THI GIỮA HỌC KÌ 2 MÔN TOÁN LỚP 7 CHÂN TRỜI SÁNG TẠO - NĂM HỌC 2024

Lưu ý:

− Các câu hỏi ở cấp độ nhận biết và thông hiểu là các câu hỏi trắc nghiệm khách quan 4 lựa chọn, trong đó có duy nhất 1 lựa chọn đúng.

− Các câu hỏi ở cấp độ thông hiểu, vận dụng và vận dụng cao là câu hỏi tự luận.

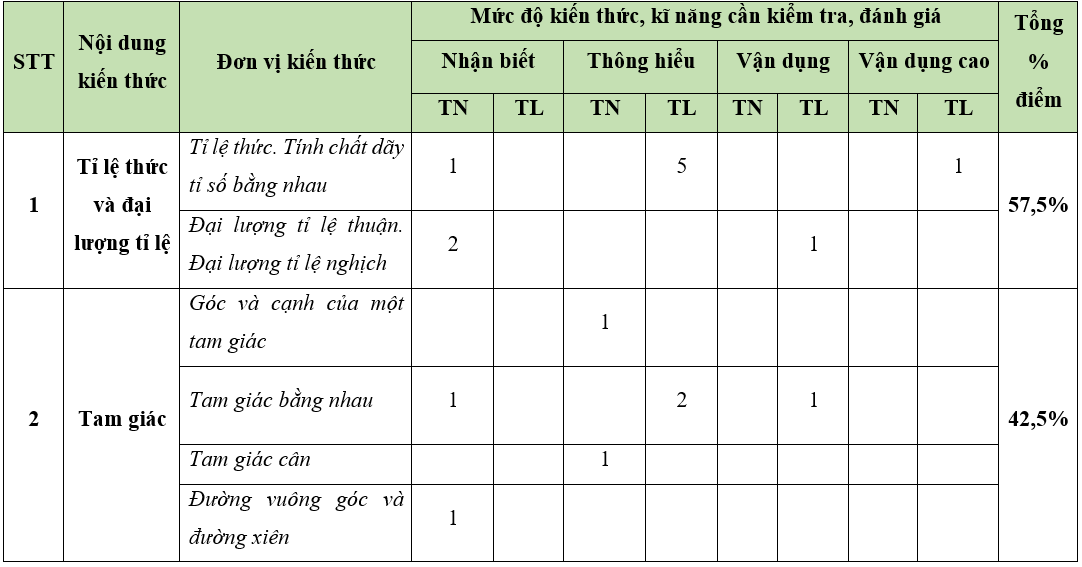
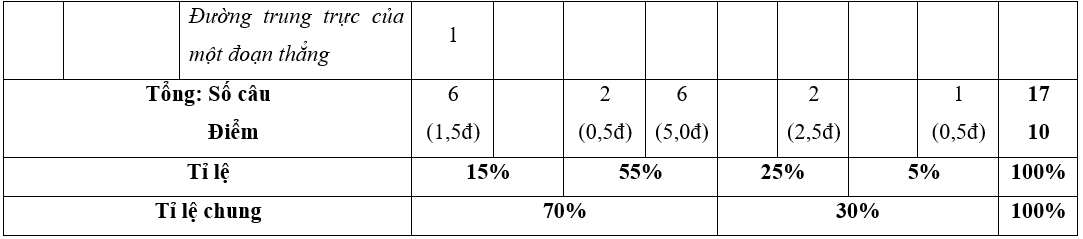
− Số điểm tính cho 1 câu trắc nghiệm là 0,25 điểm/câu; số điểm của câu tự luận được quy định trong hướng dẫn chấm nhưng phải tương ứng với tỉ lệ điểm được quy định trong ma trận.

BẢN ĐẶC TẢ MA TRẬN ĐỀ KIỂM TRA GIỮA HỌC KÌ II TOÁN – LỚP 7

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Giữa Học kì 2

Năm học ...

Môn: Toán 7

Thời gian làm bài: 90 phút

Đề thi Giữa học kì 2 Toán lớp 7 Kết nối tri thức có đáp án - Đề số 1

I. PHẦN TRẮC NGHIỆM KHÁCH QUAN (2,0 điểm)

Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây.

Câu 1. Tỉ lệ thức nào sau đây không được lập từ tỉ lệ thức $\frac{14}{8}=\frac{21}{12}$ ?

A. $\frac{14}{21}=\frac{8}{12}$

B. $\frac{21}{14}=\frac{12}{8}$ ;

C. $\frac{14}{12}=\frac{21}{8}$;

D. $\frac{12}{21}=\frac{8}{14}$.

Câu 2. Biết đại lượng y tỉ lệ thuận với đại lượng x với các cặp giá trị tương ứng trong bảng sau:

Giá trị cần điền vào “?” là

A. $\frac{-1}{5}$ ;

B. $\frac{1}{5}$ ;

C. 5;

D. −5.

Câu 3. Cho biết y tỉ lệ nghịch với x theo hệ số tỉ lệ a và khi x = –2 thì y = 4. Khi đó, hệ số a bằng bao nhiêu?

A. –2;

B. –6;

C. –8;

D. – 4.

Câu 4. Bộ ba độ dài đoạn thẳng nào sau đây tạo thành một tam giác?

A. 5 cm; 4 cm; 1 cm;

B. 3 cm; 4 cm; 5 cm;

C. 5 cm; 2 cm; 2 cm;

D. 1 cm; 4 cm; 10 cm.

Câu 5. Cho hình vẽ

Hai tam giác trên bằng nhau theo trường hợp

A. Cạnh – góc – góc;

B. Cạnh – góc – cạnh;

C. Góc – cạnh – góc;

D. Cả A, B, C đều đúng.

Câu 6. Cho hình vẽ

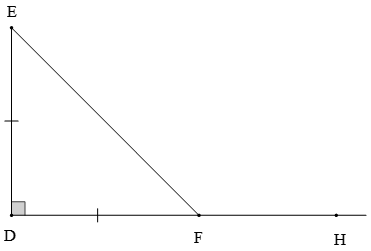
Số đo của $\widehat{EFH}$ là

A. 105°;

B. 115°;

C. 125°;

D. 135°.

Câu 7. Cho ABCD là hình chữ nhật như hình vẽ, điểm E nằm trên cạnh CD. Khẳng định nào sau đây là sai?

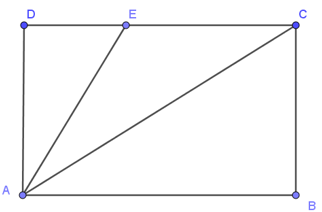
A. AE < AD;

B. AC > AD;

C. AC > AE;

D. AD < AE.

Câu 8. Điền vào chỗ trống sau: “Đường thẳng vuông góc với một đoạn thẳng tại … của nó được gọi là đường trung trực của đoạn thẳng đó”.

A. Trung trực;

B. Giao điểm;

C. Trọng tâm;

D. Trung điểm.

II. PHẦN TỰ LUẬN (8,0 điểm)

Bài 1. (1,5 điểm) Tìm số hữu tỉ x trong các tỉ lệ thức sau:

a) $\frac{-6}{x}=\frac{9}{-15}$ ;

b) $\frac{3x-7}{8}=\frac{5}{2}$ ;

c) $\frac{-4}{x}=\frac{x}{-49}$ .

Bài 2. (1,5 điểm)

a) Cho $\frac{a}{b}=\frac{6}{5}$ . Tìm a, b biết: a – b = 3.

b) Cho $\frac{x}{2}=\frac{y}{3}=\frac{z}{5}$ Tìm x, y, z biết x – 2y + 3z = 33.

Bài 3. (1,5 điểm) Ba đơn vị cùng vận chuyển 700 tấn hàng. Đơn vị A có 10 xe trọng tải mỗi xe là 5 tấn; đơn vị B có 20 xe trọng tải mỗi xe là 4 tấn; đơn vị C có 14 xe trọng tải mỗi xe là 5 tấn. Hỏi mỗi đơn vị vận chuyển được bao nhiêu tấn hàng, biết mỗi xe đều chở một số chuyến như nhau?

Bài 4. (3,0 điểm) Cho góc xOy khác góc bẹt có Ot là tia phân giác. Qua điểm H thuộc tia Ot, kẻ đường vuông góc với Ot và cắt Ox và Oy theo thứ tự A và B.

a) Chứng minh OA = OB.

b) Lấy điểm C nằm giữa O và H. Chứng minh $\widehat{ACH}=\widehat{HCB}$ .

c) AC cắt Oy ở D. Trên tia Ox lấy điểm E sao cho OE = OD. Chứng minh ba điểm B, C, E thẳng hàng.

Bài 5. (0,5 điểm) Cho tỉ lệ thức . Chứng minh rằng .

−−−−−−−−− HẾT −−−−−−−−−−

ĐÁP ÁN ĐỀ SỐ 01

I. Bảng đáp án trắc nghiệm

II. Hướng dẫn giải trắc nghiệm

Câu 1.

Từ tỉ lệ thức $\frac{14}{8}=\frac{21}{12}$ ta có thể lập được các tỉ lệ thức $\frac{14}{21}=\frac{8}{12}$; $\frac{21}{14}=\frac{12}{8}$; $\frac{12}{21}=\frac{8}{14}$ .

Do đó $\frac{14}{12}=\frac{21}{8}$ không được lập từ tỉ lệ thức $\frac{14}{8}=\frac{21}{12}$ .

Câu 2.

Đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ $k=\frac{-1}{5}$ .

Ta có $\frac{-1}{5}.1=\frac{-1}{5}$ . Do đó giá trị cần điền vào bảng là $\frac{-1}{5}$ .

Câu 4.

Ta có: 5 – 4 = 1 < 3; 5 – 3 = 2 < 4; 4 – 3 = 1 < 5.

Vậy bộ ba độ dài 3 cm; 4 cm; 5 cm có thể tạo thành một tam giác.

Câu 6.

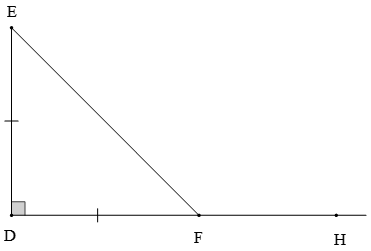
Xét ∆DEF có DE = DF nên ∆DEF cân tại D.

Mặt khác ∆DEF cân tại D có $\hat{D}=90°$

Suy ra ∆DEF vuông cân tại D.

Suy ra $\widehat{DFE}=45°$ (tính chất tam giác vuông cân)

Ta có: $\widehat{DFE}+\widehat{EFH}=180°$ (hai góc kề nhau)

Hay $45°+\widehat{EFH}=180°$

Suy ra $\widehat{EFH}=180°-45°=135°$ .

Tam giác ABC có = 90°; = = 45° nên tam giác ABC là tam giác vuông cân.

Câu 7.

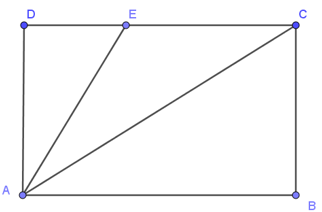
Khẳng định AE < AD là sai vì AD là đường vuông góc, AE là đường xiên.

II. PHẦN TỰ LUẬN (8,0 điểm)

Bài 1. (1,5 điểm)

a) $$\begin{gathered} \frac{-6}{x}=\frac{9}{-15} \\ x=\frac{(-6).(-15)}{9} \end{gathered}$$

x = 10

Vậy x = 10.

b) $$\begin{gathered} \frac{3x-7}{8}=\frac{5}{2} \\ 3x-7=\frac{8.5}{2} \end{gathered}$$

3x – 7 = 20

3x = 27

x = 9

Vậy x = 9.

c) $\frac{-4}{x}=\frac{x}{-49}$

x² = (−4) . (−49)

x² = 196

x = 14 hoặc x = −14

Vậy x ∈ {14; −14}.

Bài 2. (1,5 điểm)

a) Ta có $\frac{a}{b}=\frac{6}{5}$ suy ra $\frac{a}{6}=\frac{b}{5}$ .

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

$\frac{a}{6}=\frac{b}{5}=\frac{a-b}{6-5}=\frac{3}{1}=3$.

Do đó a = 6 . 3 = 18; b = 5 . 3 = 15.

Vậy a = 18; b = 15.

b) Ta có $\frac{x}{2}=\frac{y}{3}=\frac{z}{5}$ suy ra $\frac{x}{2}=\frac{2y}{6}=\frac{3z}{15}$ .

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

$\frac{x}{2}=\frac{2y}{6}=\frac{3z}{15}=\frac{x-2y+3z}{2-6+15}=\frac{33}{11}=3$.

Do đó x = 3 . 2 = 6; y = 3 . 6 = 18; z = 3 . 15 = 45.

Vậy x = 6; y = 18; z = 45.

Bài 3. (1,5 điểm)

Gọi x, y, z (tấn) lần lượt là khối lượng hàng các đơn vị A, B, C vận chuyển (x, y, z > 0).

Theo đề bài ta suy ra: $\frac{x}{50}=\frac{y}{80}=\frac{z}{70}$ .

Ba đơn vị cùng vận chuyển 700 tấn hàng nên x + y + z = 700.

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

$\frac{x}{50}=\frac{y}{80}=\frac{z}{70}=\frac{x+y+z}{50+80+70}=3,5$.

Do đó x = 50 . 3,5 = 275; y = 80 . 3,5 = 280; z = 70 . 2,5 = 245 (thỏa mãn).

Vậy đơn vị A, B, C lần lượt vận chuyển được 275 tấn hàng, 280 tấn hàng và 245 tấn hàng.

Bài 4. (3,0 điểm)

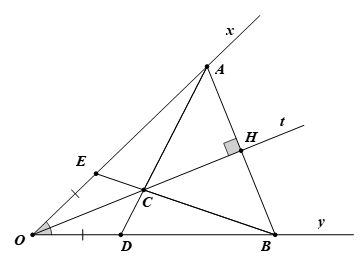
a) Xét ∆AHO và ∆BHO có:

$\widehat{AHO}=\widehat{BHO}=90°$;

Cạnh OH chung;

$\widehat{AOH}=\widehat{BOH}$(vì Ot là tia phân giác của $\widehat{xOy}$ ).

Do đó ∆AHO = ∆BHO (cạnh huyền – góc nhọn).

Suy ra OA = OB (hai cạnh tương ứng).

b) Xét ∆AHC và ∆BHC có:

$\widehat{AHC}=\widehat{BHC}=90°$;

AH = BH (vì ∆AHO = ∆BHO);

Cạnh HC chung

Do đó ∆AHC = ∆BHC (hai cạnh góc vuông).

Suy ra $\widehat{ACH}=\widehat{HCB}$ (hai góc tương ứng).

c) Xét ∆OEC và ∆ODC có:

OE = OD (giả thiết)

$\widehat{EOC}=\widehat{DOC}$ (vì Ot là tia phân giác của $\widehat{xOy}$ ).

Cạnh OC chung

Do đó ∆OEC = ∆ODC (c.g.c)

Suy ra $\widehat{ECO}=\widehat{OCD}$ (hai góc tương ứng)

Ta có $\widehat{OCD}=\widehat{ACH}$ (đối đỉnh) hay $\widehat{ECO}=\widehat{OCD}=\widehat{ACH}=\widehat{HCB}$

Vì ba điểm A, C, D thẳng hàng nên $\widehat{ACH}+\widehat{HCB}+\widehat{MCD}=180°$

hay $\widehat{ECO}+\widehat{OCD}+\widehat{BCD}=180°$ hay ba điểm E, C, B thẳng hàng.

Bài 5. (0,5 điểm)

Vì $\frac{a}{b}=\frac{c}{d}$ nên ad = bc.

Ta có: ab(c² – d²) = abc² – abd² = acbc – adbd;

cd(a² – b²) = cda² – cdb² = acad – bcbd.

Do đó ab(c² – d²) = cd(a² – b²).

Suy ra $\frac{ab}{cd}=\frac{a^2-b^2}{c^2-d^2}$ (đpcm).

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Giữa Học kì 2

Năm học ...

Môn: Toán 7

Thời gian làm bài: 90 phút

Đề thi Giữa học kì 2 Toán lớp 7 Kết nối tri thức có đáp án - Đề số 2

I. PHẦN TRẮC NGHIỆM KHÁCH QUAN (2,0 điểm)

Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây:

Câu 1. Thay tỉ số 1,25 : 3,45 bằng tỉ số giữa các số nguyên ta được

A. 12,5 : 34,5;

B. 29 : 65;

C. 25 : 69;

D. 1 : 3.

Câu 2. Biết y tỉ lệ thuận với x theo hệ số tỉ lệ k = 2. Khi x = –3 thì giá trị của y bằng bao nhiêu?

A. –6;

B. 0;

C. –9;

D. –1.

Câu 3. Cho x và y là hai đại lượng tỉ lệ nghịch với nhau và khi x = –12 thì y = 8. Khi x = 3 thì y bằng

A. –32;

B. 32;

C. –2;

D. 2.

Câu 4. Cho hình vẽ sau:

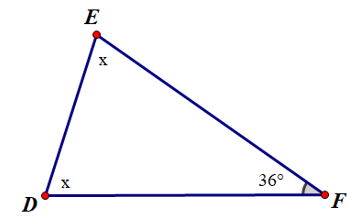
Số đo x là

A. 18°;

B. 72°;

C. 36°;

D. Không xác định được.

Câu 5. Hai tam giác bằng nhau là

A. Hai tam giác có ba cặp cạnh tương ứng bằng nhau;

B. Hai tam giác có ba cặp góc tương ứng bằng nhau;

C. Hai tam giác có ba cặp cạnh, ba cặp góc tương ứng bằng nhau;

D. Hai tam giác có hai cạnh bằng nhau.

Câu 6. Một tam giác cân có góc ở đáy bằng 40° thì số đo góc ở đỉnh là

A. 50°;

B. 40°;

C. 140°;

D. 100°.

Câu 7. Cho tam giác MNP có: MN < MP, MD ⊥ NP. Khẳng định nào sau đây là đúng?

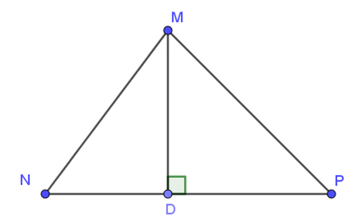
A. DN = DP;

B. MN = MP;

C. MD > MN;

D. MD < MP.

Câu 8. Điền vào chỗ trống sau: “Điểm … hai đầu mút của một đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó”

A. thuộc;

B. cách đều;

C. nằm trên;

D. nằm trong.

II. PHẦN TỰ LUẬN (8,0 điểm)

Bài 1. (1,5 điểm) Tìm số hữu tỉ x trong các tỉ lệ thức sau:

a) $\frac{5}{6}:x=20:3$;

b) $\frac{9x-1}{9}=\frac{5}{3}$ ;

c) $\frac{x+11}{14-x}=\frac{2}{3}$ .

Bài 2. (1,5 điểm)

a) Tìm giá trị a, b thỏa mãn 3a = 4b và b – a = 5.

b) Cho $\frac{a}{2}=\frac{b}{3}; \frac{b}{5}=\frac{c}{4}$ . Tìm a, b, c biết a + b + c = –74.

Bài 3. (1,5 điểm) Một ô tô đi từ A lúc 8 giờ. Đến 9 giờ một ô tô khác cũng đi xe từ A. Xe thứ nhất đến B lúc 2 giờ chiều. Xe thứ hai đến B sớm hơn xe thứ nhất nửa giờ. Tính vận tốc mỗi xe biết rằng vận tốc xe thứ hai lớn hơn vận tốc xe thứ nhất là 20 km/h.

Bài 4. (3,0 điểm) Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm M, trên tia đối tia của tia CB lấy điểm N sao cho BM = CN. Kẻ BE ⊥ AM (E ∈ AM), CF ⊥ AN (F ∈ AN).

a) Chứng minh rằng ∆BME = ∆CNF.

b) EB và FC kéo dài cắt nhau tại O. Chứng minh AO là tia phân giác của góc MAN

c) Qua M kẻ đường thẳng vuông góc với AM, qua N kẻ đường thẳng vuông góc với AN, chúng cắt nhau ở H. Chứng minh ba điểm A, O, H thẳng hàng.

Bài 5. (0,5 điểm) Cho tỉ lệ thức $\frac{a}{b}=\frac{c}{d}$ . Chứng minh rằng $\frac{a-2b}{b}=\frac{c-2d}{d}$ .

−−−−−−−−− HẾT −−−−−−−−−−

ĐÁP ÁN ĐỀ SỐ 02

I. Bảng đáp án trắc nghiệm

II. Hướng dẫn giải trắc nghiệm

Câu 1.

Ta có 1,25:3,45 = $\frac{1,25}{3,45}=\frac{25}{69}$.

Câu 3.

Hệ số tỉ lệ là: a = (–12) . 8 = –96.

Khi x = 3 thì y = –96 : 3 = –32.

Câu 4.

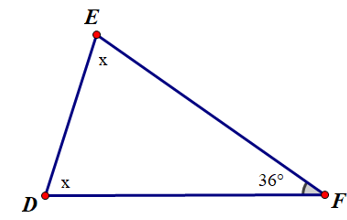
Áp dụng định lý về tổng số đo ba góc của tam giác ta có:

$\hat{D}+\hat{E}+\hat{F}$+ + = 180°

Suy ra x + x + 36° = 180°

Hay 2x = 144°

Do đó x = 72°.

Câu 6.

Giả sử tam giác ABC cân tại A ta có: = 40°.

Xét tam giác ABC có:

$\hat{A}+\hat{B}+\hat{C}$= 180° (tổng ba góc trong một tam giác).

Do đó $\hat{A}$= 180° − $\hat{B}$ − $\hat{C}$ = 180° − 40° − 40° = 100°.

Vậy số đo góc ở đỉnh là 100°.

II. PHẦN TỰ LUẬN (7,0 điểm)

Bài 1. (1,5 điểm)

a) $$\begin{gathered} \frac{5}{6}:x=20:3 \\ \frac{{\displaystyle \frac{5}{6}}}{x}=\frac{20}{3} \\ x=\frac{{\displaystyle \frac{5}{6}}:3}{20} \\ x=\frac{{\displaystyle \frac{5}{2}}}{20} \\ x=\frac{1}{8} \end{gathered}$$

Vậy x = $\frac{1}{8}$.

b)

$\frac{9x-1}{9}=\frac{5}{3}$

$9x-1=\frac{5.9}{3}$

9x – 1 = 15

9x = 16

x = $\frac{16}{9}$

Vậy x = $\frac{16}{9}$.

c)

$\frac{x+11}{14-x}=\frac{2}{3}$

3(x + 11) = 2(14 – x)

3x + 33 = 28 – 2x

3x + 2x = 28 – 33

5x = –5

x = –1

Vậy x = –1.

Bài 2. (1,5 điểm)

a) Từ 3a = 4b, ta suy ra $\frac{a}{4}=\frac{b}{3}$ .

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

$\frac{a}{4}=\frac{b}{3}=\frac{b-a}{3-4}=\frac{5}{-1}=-5$.

Suy ra a = (–5) . 4 = –20; b = (–5) . 3 = –15.

Do đó a = –20; b = –15.

b) Ta có:

⦁ $\frac{a}{2}=\frac{b}{3}$ suy ra $\frac{a}{2.5}=\frac{b}{3.5}$ hay $\frac{a}{10}=\frac{b}{15}$ (1)

⦁ $\frac{b}{5}=\frac{c}{4}$ suy ra $\frac{b}{5.3}=\frac{c}{4.3}$ hay $\frac{b}{15}=\frac{c}{12}$ (2)

Từ (1), (2) suy ra $\frac{a}{10}=\frac{b}{15}=\frac{c}{12}$ .

Áp dụng tính chất dãy tỉ sổ bằng nhau, ta có:

$\frac{a}{10}=\frac{b}{15}=\frac{c}{12}=\frac{a+b+c}{10+15+12}=\frac{-74}{37}=-2$.

Suy ra a = (–2) . 10 = –20; b = (–2) . 15 = –30; c = (–2) . 12 = –24.

Do đó a = –20; b = –30; c = –24.

Bài 2. (1,5 điểm)

Trên cùng một quãng đường, vận tốc và thời gian tỉ lệ nghịch với nhau.

Gọi v₁, t₁ lần lượt là vận tốc và thời gian của xe I; v₂, t₂ lần lượt là vận tốc và thời gian của xe II.

Thời gian xe I đi hết đoạn đường AB là:

14 – 8 = 6 (giờ).

Thời gian xe II đi hết đoạn đường AB là:

(14 – 0,5) – 9 = 4,5 (giờ).

Ta có $\frac{v_1}{v_2}=\frac{t_2}{t_1}=\frac{4,5}{6}=\frac{3}{4}$ hay $\frac{v_1}{3}=\frac{v_2}{4}$ .

Vì vận tốc xe thứ hai lớn hơn vận tốc xe thứ nhất là 20 km/h nên v₂ – v₁ = 20.

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

$\frac{v_1}{3}=\frac{v_2}{4}=\frac{v_2-v_1}{4-3}=\frac{20}{1}=20$.

Suy ra v₁ = 20 . 3 = 60; v₂ = 20 . 4 = 80.

Vậy vận tốc của xe thứ nhất là 60 km/h, vận tốc của xe thứ hai là 80 km/h.

Bài 4. (3,0 điểm)

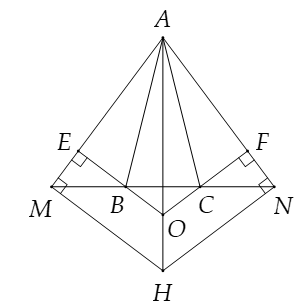
a) Vì ∆ABC cân tại A nên $\widehat{ABC}=\widehat{ACB}$ suy ra $\widehat{ABM}=\widehat{ACN}$ .

Xét ∆ABM và ∆CAN có:

AB = AC (vì ∆ABC cân tại A)

$\widehat{ABM}=\widehat{ACN}$(chứng minh trên)

BM = CN (giả thiết)

Do đó ∆ABM = ∆CAN (c.g.c).

Suy ra BM = CN (hai cạnh tương ứng); $\widehat{AMB}=\widehat{ANC}$ (hai góc tương ứng).

Xét ∆BME và ∆CNF có:

$\widehat{BEM}=\widehat{CFN}=90°$

BM = CN (chứng minh trên)

$\widehat{AMB}=\widehat{ANC}$ (chứng minh trên)

Do đó ∆BME = ∆CNF (cạnh huyền – góc nhọn).

b) Từ câu b: ∆BME = ∆CNF suy ra ME = NF.

Mà AM = AN nên AE = AF.

Ta lại có $\widehat{EBM}=\widehat{FCN}$ suy ra $\widehat{OBC}=\widehat{OCB}$ .

Do đó ∆OBC cân tại O từ đó OB = OC suy ra OE = OF.

Xét ∆AEO và ∆AFO có:

AE = AF (chứng minh trên)

$\widehat{AEO}=\widehat{AFO}=90°$

OE = OF (chứng minh trên)

Do đó ∆AEO = ∆AFO (c.g.c)

Suy ra $\widehat{OAE}=\widehat{OAF}$ (hai góc tương ứng).

Vậy AO là tia phân giác của góc MAN.

c) Xét ∆AMH và ∆ANH có: $\widehat{AMH}=\widehat{ANH}=90°$

Cạnh AH chung

AM = AN (chứng minh trên)

Do đó ∆AMH = ∆ANH (cạnh huyền – cạnh góc vuông)

Suy ra $\widehat{MAH}=\widehat{NAH}$ (hai góc tương ứng)

Suy ra AH là phân giác góc MAN.

Mặt khác AO là phân giác góc MAN nên AH và AO trùng nhau.

Do đó ba điểm A, O, H thẳng hàng.

Bài 5. (0,5 điểm)

Đặt $\frac{a}{b}=\frac{c}{d}=k$ suy ra a = bk, c = dk.

Ta có $\frac{a-2b}{b}=\frac{bk-2b}{b}=\frac{b(k-2)}{b}=k-2$ ;

$\frac{c-2d}{d}=\frac{dk-2d}{d}=\frac{d(k-2)}{d}=k-2$.

Vậy $\frac{a-2b}{b}=\frac{c-2d}{d}$ (đpcm).

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Giữa Học kì 2

Năm học ...

Môn: Toán 7

Thời gian làm bài: 90 phút

Đề thi Giữa học kì 2 Toán lớp 7 Kết nối tri thức - Đề số 3

I. PHẦN TRẮC NGHIỆM KHÁCH QUAN (2,0 điểm)

Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây.

Câu 1. Cho . Số vào ô trống để được tỉ lệ thức đúng là

A. 4;

B. −4;

C. 2;

D. 8.

Câu 2. Cho hai đại lượng c và d liên hệ với nhau bởi công thức c = 25d. Phát biểu nào sau đây đúng?

A. c tỉ lệ thuận với d theo hệ số tỉ lệ là –25;

B. c tỉ lệ thuận với d theo hệ số tỉ lệ là $\frac{1}{25}$ ;

C. d tỉ lệ thuận với c theo hệ số tỉ lệ là $\frac{1}{25}$ ;

D. d tỉ lệ thuận với c theo hệ số tỉ lệ là 25.

Câu 3. Cho hại đại lượng x và y tỉ lệ nghịch với nhau và khi x = 2 thì y = 5. Khi đó, hai đại lượng x và y tỉ lệ nghịch với nhau theo hệ số tỉ lệ a bằng

A. 10;

B. $\frac{2}{5}$ ;

C. –10;

D. $\frac{5}{2}$ .

Câu 4. Cho hình vẽ

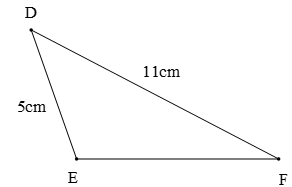
Độ dài cạnh EF bằng

A. 3 cm;

B. 5 cm;

C. 6 cm;

D. 8 cm.

Câu 5. Cho hai tam giác MNP và IKJ có: MN = IK; NP = KJ; MP = JI; $\hat{M}=\hat{I}$; $\hat{N}=\hat{K}$ . Khẳng định nào sau đây là đúng?

A. ∆MNP = ∆IJK;

B. ∆MNP = ∆IKJ;

C. ∆MNP = ∆KIJ;

D. ∆MNP = ∆JKL.

Câu 6. Cho tam giác ABC có $\hat{B}$ = $\hat{C}$ = 45°. Khi đó, tam giác ABC là tam giác gì? Chọn kết luận đúng nhất.

A. Tam giác cân;

B. Tam giác vuông;

C. Tam giác đều;

D. Tam giác vuông cân.

Câu 7. Trong tam giác ABC có chiều cao AH. Khẳng định nào sau đây là đúng?

A. Nếu BH < HC thì AB < AC;

B. Nếu AB < AC thì BH < HC;

C. Nếu BH = HC thì AB = AC;

D. Cả A, B, C đều đúng.

Câu 8. Cho hình vẽ sau.

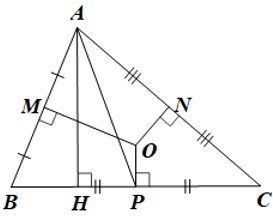
Tổng số đường trung trực có trong hình vẽ là

A. 2;

B. 3;

C. 4;

D. 5.

II. PHẦN TỰ LUẬN (8,0 điểm)

Bài 1. (1,5 điểm) Tìm số hữu tỉ x trong các tỉ lệ thức sau:

a) $\frac{3,5}{15}=\frac{-2}{x}$ ;

b) $\frac{3}{5}:\frac{2x}{15}=\frac{1}{2}:\frac{4}{5}$ ;

c) $\frac{x-1}{x+2}=-1$ .

Bài 2. (1,5 điểm)

a) Cho $\frac{x}{3}=\frac{y}{2}$ . Tìm x, y biết: x + y = 90.

b) Cho $\frac{x}{2}=\frac{y}{3}; \frac{y}{6}=\frac{z}{11}$ . Tìm x, y, z biết: x + y + z = 105.

Bài 2. (1,5 điểm) Học sinh của 3 lớp 7 được giao trồng 36 cây. Sau khi lớp 7A trồng được $\frac{1}{5}$ số cây của lớp. Lớp 7B trồng được $\frac{1}{3}$ số cây của lớp và lớp 7C trồng được $\frac{3}{7}$ số cây của lớp thì số cây còn lại của mỗi lớp bằng nhau. Hỏi mỗi lớp trồng được bao nhiêu cây?

Bài 4. (3,0 điểm) Cho góc bẹt xOy có tia phân giác Ot. Trên tia Ot lấy hai điểm A và B (A nằm giữa O và B). Lấy điểm C ∈ Ox sao cho OC = OB, lấy điểm D ∈ Oy sao cho

a) Chứng minh AC = BD và AC ⊥ BD.

b) Gọi M, N lần lượt là trung điểm của AC và BD. Chứng minh OM = ON.

c) Tính các góc của tam giác MON.

d) Chứng minh AD ⊥ BC.

Bài 5. (0,5 điểm) Cho tỉ lệ thức $\frac{a}{b}=\frac{c}{d}$ . Chứng minh rằng $\frac{7a^2+3ab}{11a^2-8b^2}=\frac{7c^2+3cd}{11c^2-8d^2}$ .

−−−−−−−−− HẾT −−−−−−−−−−

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Giữa Học kì 2

Năm học ...

Môn: Toán 7

Thời gian làm bài: 90 phút

Đề thi Giữa học kì 2 Toán lớp 7 Kết nối tri thức - Đề số 4

I. PHẦN TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)

Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây:

Câu 1. Tỉ lệ thức nào sau đây không được lập từ tỉ lệ thức $\frac{x}{2}=\frac{a}{b}$ ?

A.$\frac{x}{a}=\frac{2}{b}$ ;

B. $\frac{x}{b}=\frac{a}{2}$ ;

C.$\frac{b}{2}=\frac{a}{x}$ ;

D.$\frac{b}{a}=\frac{2}{x}$ .

Câu 2. Với dãy tỉ số bằng nhau $\frac{x}{a}=\frac{y}{b}=\frac{z}{c}$ ta có thể viết:

A. x : y : z = a : c : b;

B. a : b : c = z : y : x;

C. x : y : z = a : b : c;

D. x : b : z = a : y : c.

Câu 3. Giá trị x, y, z thỏa mãn $\frac{x}{6}=\frac{y}{4}=\frac{z}{3}$ và x – y + z = 35 là:

A. x = 42, y = 28, z = 21;

B. x = 21, y = 28, z = 42;

C. x = 28, y = 42, z = 21;

D. x = 42, y = 21, z = 28.

Câu 4. Chia số 340 thành ba phần tỉ lệ thuận với $\frac{3}{16}; \frac{1}{2}; \frac{1}{4}$ và ta được số bé nhất là:

A.$\frac{544}{3}$ ;

B. –68;

C. $\frac{272}{3}$ ;

D. 68.

Câu 5. Các giá trị tương ứng của hai đại lượng x và y được cho trong các bảng dưới đây. Bảng nào thể hiện hai đại lượng x và y tỉ lệ nghịch với nhau?

A.

B.

C.

D.

Câu 6. Trong các bộ ba độ dài đoạn thẳng dưới đây, bộ ba có thể là độ dài ba cạnh của một tam giác là

A. 6 cm, 2 cm, 3 cm;

B. 8 cm, 4 cm, 4 cm;

C. 7 cm, 9 cm, 5 cm;

D. 8 cm, 5 cm, 3 cm.

Câu 7. Cho hình vẽ

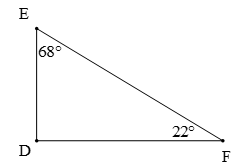
Chọn khẳng định đúng.

A. ∆DEF là tam giác vuông;

B. ∆DEF là tam giác nhọn;

C. ∆DEF là tam giác tù;

D. Cả A, B, C đều sai.

Câu 8. Cho hình vẽ

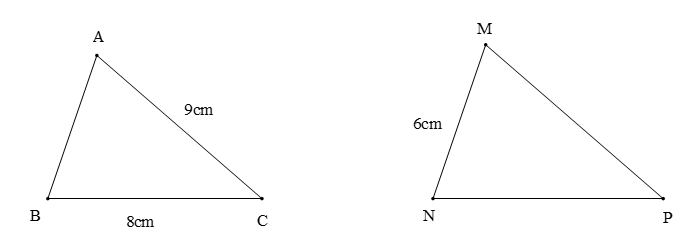
Biết ∆ABC = ∆MNP. Chu vi ∆MNP là

A. 12 cm;

B. 18 cm;

C. 23 cm;

D. 26 cm.

Câu 9. Cho ∆ABC cân tại A có BC = 9 cm; chu vi ∆ABC bằng 25 cm. Chọn khẳng định sai.

A.$\hat{A}>\hat{B}$ ;

B. $\hat{B}=\hat{C}>\hat{A}$ ;

C. $\hat{B}=\hat{C}$ ;

D. $\hat{A}>\hat{C}$ .

Câu 10. Một tam giác cân có độ dài hai cạnh 3,9 cm và 7,9 cm. Chu vi của tam giác này là

A. 15,5 cm;

B. 17,8 cm;

C. 19,7 cm;

D. 20,9 cm.

Câu 11. Cho hình vẽ dưới đây:

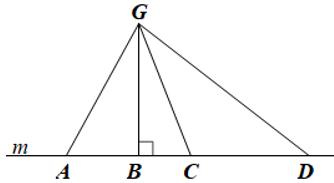
Số đường xiên kẻ từ điểm G đến đường thẳng m trong hình trên là

A. 1;

B. 2;

C. 3;

D. 4.

Câu 12. Cho các hình vẽ sau.

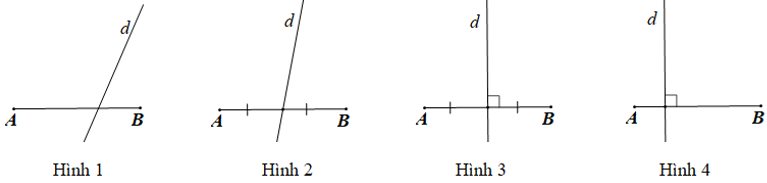
Hình vẽ nào minh họa đường thẳng d là đường trung trực của đoạn thẳng AB?

A. Hình 1;

B. Hình 2;

C. Hình 3;

D. Hình 4.

II. PHẦN TỰ LUẬN (7,0 điểm)

Bài 1. (1,5 điểm) Tìm số hữu tỉ x trong các tỉ lệ thức sau:

a) $\frac{25}{3}:x=2:9$ ;

b) 0,5:2 = 3: (2x+7);

c) $\frac{12}{\left|x-5\right|}=\frac{6}{7}$ .

Bài 2. (1,5 điểm) Một công việc dự định giao cho 3 người làm trong 12 ngày nhưng cuối cùng chỉ có 2 người làm, vì vậy họ phải làm thêm mỗi ngày 1 giờ và hoàn thành công việc trong 16 ngày. Biết rằng năng suất lao động của họ là như nhau. Hỏi họ phải làm mỗi ngày mấy giờ.

Bài 3. (3,5 điểm) Cho tam giác ABC có $\hat{A}=40°$, AB = AC và H là trung điểm của BC. Đường thẳng d đi qua trung điểm của AC và vuông với với AC cắt tia CB tại M.

a) Tính $\widehat{MAH}$

b) Trên tia đối của tia lấy điểm sao cho AN = BM. Chứng minh AM = CN.

c) Vẽ CI ⊥ MN tại I. Chứng minh I là trung điểm MN.

d) AH cắt đường thẳng d tại K. Chứng minh ba điểm C, I, K thẳng hàng .

Bài 4. (0,5 điểm) Cho tỉ lệ thức $\frac{a}{b}=\frac{b}{c}=\frac{c}{d}$ . Chứng minh rằng ${\left(\frac{a+b+c}{b+c+d}\right)}^3=\frac{a}{d}$ .

−−−−−−−−− HẾT −−−−−−−−−−

Để xem trọn bộ Đề thi Toán 7 Chân trời sáng tạo có đáp án, Thầy/ cô vui lòng Tải xuống!

Xem thêm đề thi các môn lớp 7 bộ sách Chân trời sáng tạo hay, có đáp án chi tiết:

Đề thi Giữa Học kì 2 Tin học lớp 7 Chân trời sáng tạo (10 đề có đáp án + ma trận)

Đề thi Giữa Học kì 2 Văn lớp 7 Chân trời sáng tạo (10 đề có đáp án + ma trận)

Đề thi Giữa học kì 2 Tiếng Anh lớp 7 Friends plus (10 đề có đáp án + ma trận) | Chân trời sáng tạo

Đề thi Giữa Học kì 2 Khoa học tự nhiên lớp 7 Chân trời sáng tạo (10 đề có đáp án + ma trận)

Đề thi Giữa Học kì 2 Lịch sử và Địa lí lớp 7 Chân trời sáng tạo (10 đề có đáp án + ma trận)

Đề thi Giữa Học kì 2 Giáo dục công dân lớp 7 Chân trời sáng tạo (10 đề có đáp án + ma trận)

Đề thi Giữa Học kì 2 Công nghệ lớp 7 Chân trời sáng tạo (10 đề có đáp án + ma trận)