Chuyên đề Toán 12 Bài 2 (Chân trời sáng tạo): Vận dụng đạo hàm giải bài toán tối ưu

Giải Chuyên đề Toán 12 Bài 2: Vận dụng đạo hàm giải bài toán tối ưu

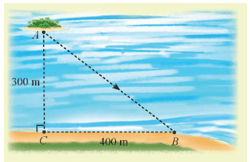
Khởi động trang 15 Chuyên đề Toán 12: Một người đang ở vị trí A muốn đi đến vị trí B trên bờ hồ như hình bên. Biết rằng người đó chèo thuyền với tốc độ 50 m/phút và chạy bộ với tốc độ 100 m/phút. Nếu người đó chèo thuyền thẳng từ A đến B thì tốn bao nhiêu thời gian? Có phương án nào tốn ít thời gian hơn không?

Lời giải:

Sau bài học này, ta giải quyết được bài toán trên như sau:

Áp dụng định lý Pythagore, ta tính được AB = 500 m.

Do đó, nếu người đó chèo thuyền thẳng từ A đến B thì tốn $\frac{500}{50}=10$phút.

Ta xem xét phương án sau:

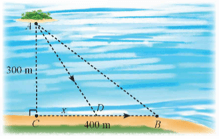
Giả sử người đó chèo thuyền thẳng đến điểm D nằm giữa B và C và cách C một đoạn x (m), rồi chạy bộ thẳng đến B.

Ta cần tìm giá trị của x để người đó tốn ít thời gian nhất.

Ta có: $AD=\sqrt{x^2+{300}^2}=\sqrt{x^2+90000}$(m); DB = 400 – x (m) với 0 ≤ x ≤ 400.

Thời gian người đó tiêu tốn là

$t=\frac{\sqrt{x^2+90000}}{50}+\frac{400-x}{100}=\frac{1}{100}\left(2\sqrt{x^2+90000}+400-x\right)$ (phút).

Xét hàm số $y=2\sqrt{x^2+90000}+400-x$ với 0 ≤ x ≤ 400, ta có:

$y^{\text{'}}=\frac{2x}{\sqrt{x^2+90000}}-1$;

y' = 0 ⇔ $\frac{2x}{\sqrt{x^2+90000}}-1=0\iff 2x=\sqrt{x^2+90000}$ ⇔ 4x² = x² + 90 000

⇔ x² = 30 000 ⇔ x = $100\sqrt{3}$ ∈ [0; 400].

Ta có y(0) = 1 000; $y\left(100\sqrt{3}\right)=300\sqrt{3}+400\approx 920$; y(400) = 1 000.

Vậy $\underset{\left[0;400\right]}{\min }y=y\left(100\sqrt{3}\right)\approx 920$.

Suy ra giá trị nhỏ nhất của t là $\frac{920}{100}=\mathrm{9,2}$(phút), đạt được khi x = $100\sqrt{3}$ ≈ 173 (m).

Do đó, người đó tốn ít thời gian nhất khi x = $100\sqrt{3}$ ≈ 173 (m).

Nhận thấy 9,2 phút < 10 phút nên người đó chèo thuyền từ A thẳng đến điểm D nằm giữa B và C và cách C một đoạn xấp xỉ bằng 173 m, rồi chạy bộ thẳng đến B là phương án tốn ít thời gian nhất.

1. Vận dụng đạo hàm giải bài toán tối ưu

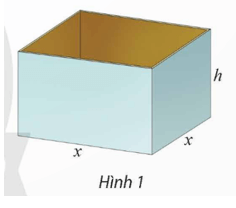
Khám phá trang 15 Chuyên đề Toán 12: Người ta muốn sản xuất những chiếc thùng có dạng hình hộp chữ nhật không nắp, có đáy là hình vuông và thể tích chứa là 500 dm³ (Hình 1). Biết rằng chiều cao của thùng trong khoảng từ 3 dm đến 10 dm.

a) Nếu gọi độ dài cạnh đáy của thùng là x (dm), chiều cao của thùng là h (dm) thì tổng diện tích các mặt của thùng, kí hiệu S, có thể được biểu thị bằng biểu thức nào?

b) Có thể biểu thị tổng diện tích S theo x không? Biến x nhận giá trị trong miền nào?

c) Với giá trị nào của x thì S có giá trị nhỏ nhất?

Lời giải:

a) Tổng diện tích các mặt của thùng là S = 4xh + x² (dm²).

b) Thể tích của thùng là V = x²h = 500 (dm³).

Suy ra $h=\frac{500}{x^2}$(dm).

Vì 3 ≤ h ≤ 10 nên $3\le \frac{500}{x^2}\le 10$, suy ra $5\sqrt{2}\le x\le \frac{10\sqrt{15}}{3}$

Khi đó, tổng diện tích các mặt của thùng là

S(x) = $\frac{2000}{x}+x^2$ (dm²) với $x\in \left[5\sqrt{2};\frac{10\sqrt{15}}{3}\right]$.

c) Xét hàm số S(x) = $\frac{2000}{x}+x^2$ (dm²) với $x\in \left[5\sqrt{2};\frac{10\sqrt{15}}{3}\right]$

Ta có S'(x) = $\frac{-2000}{x^2}+2x$;

Trên khoảng $\left(5\sqrt{2};\frac{10\sqrt{15}}{3}\right)$, S'(x) = 0 ⇔ x = 10.

Có $S\left(5\sqrt{2}\right)=200\sqrt{2}+50$; S(10) = 300; $S\left(\frac{10\sqrt{15}}{3}\right)=40\sqrt{15}+\frac{500}{3}$.

Do đó, $\underset{\left[5\sqrt{2};\frac{10\sqrt{15}}{3}\right]}{\min }S\left(x\right)=300$ tại x = 10.

Vậy với x = 10 dm thì S có giá trị nhỏ nhất.

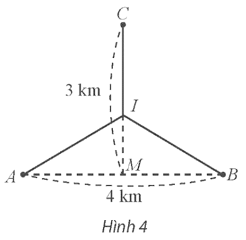
Thực hành 1 trang 17 Chuyên đề Toán 12: Hai nhà máy được đặt tại các vị trí A và B cách nhau 4 km. Nhà máy xử lí nước thải được đặt ở vị trí C trên đường trung trực của đoạn thẳng AB, cách trung điểm M của đoạn thẳng AB một khoảng là 3km. Người ta muốn làm đường ống dẫn nước thải từ hai nhà máy A, B đến nhà máy xử lí nước thải C gồm các đoạn thẳng AI, BI và IC, với I là vị trí nằm giữa M và C (Hình 4). Cần chọn vị trí điểm I như thế nào để tổng độ dài đường ống nhỏ nhất? Tìm giá trị nhỏ nhất đó.

Lời giải:

Đặt IM = x (km, 0 ≤ x ≤ 3).

Suy ra IC = 3 – x (km).

Vì M là trung điểm của AB nên MA = MB = 2 km.

Áp dụng định lí Pythagore trong các tam giác vuông AMI và BMI, ta có:

IA = IB = $\sqrt{x^2+2^2}=\sqrt{x^2+4}$ (km).

Tổng độ dài đường ống dẫn nước thải là

d = IA + IB + IC = $2\sqrt{x^2+4}+3-x$ (km).

Xét hàm số y = $2\sqrt{x^2+4}+3-x$ với 0 ≤ x ≤ 3, ta có:

y' = $\frac{2x}{\sqrt{x^2+4}}-1$;

y' = 0 ⇔ $\frac{2x}{\sqrt{x^2+4}}-1=0$$\iff \sqrt{x^2+4}=2x\iff x^2+4=4x^2$

⇔ 3x² = 4 ⇒ x = $\frac{2\sqrt{3}}{3}\in \left[0;3\right]$.

Ta có y(0) = 7; $y\left(\frac{2\sqrt{3}}{3}\right)=3+2\sqrt{3}$; y(3) = $2\sqrt{13}$.

Do đó, $\underset{\left[0;3\right]}{\min }y=y\left(\frac{2\sqrt{3}}{3}\right)=3+2\sqrt{3}\approx \mathrm{6,46}$.

Suy ra giá trị nhỏ nhất của d khoảng 6,46 km, đạt được khi $x=\frac{2\sqrt{3}}{3}\approx \mathrm{1,15}$(km).

Vậy cần chọn vị trí điểm I đặt cách vị trí M (trung điểm của AB) một khoảng xấp xỉ bằng 1,15 km thì tổng độ dài đường ống dẫn nước thải nhỏ nhất và giá trị nhỏ nhất này xấp xỉ bằng 6,46 km.

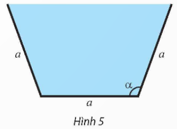
Thực hành 2 trang 18 Chuyên đề Toán 12: Mặt cắt ngang của một máng dẫn nước là một hình thang cân có độ dài đáy bé bằng độ dài cạnh bên và bằng a (cm) không đổi (Hình 5). Gọi α là một góc của hình thang cân tạo bởi đáy bé và cạnh bên $\left(\frac{\pi }{2}\le \alpha <\pi \right)$. Tìm α để diện tích mặt cắt ngang của máng lớn nhất.

Lời giải:

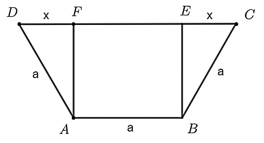
Gọi tên các điểm như hình vẽ dưới đây.

Kẻ các đường cao AF, BE của hình thang cân ABCD.

Ta chứng minh được ABEF là hình chữ nhật và DF = EC.

Khi đó ta có EF = AB = a (cm).

Đặt DF = EC = x (cm, 0 ≤ x < a).

Ta có DC = DF + FE + EC = x + a + x = 2x + a (cm).

Áp dụng định lí Pythagore ta tính được $AF=\sqrt{A{D}^2-D{F}^2}=\sqrt{a^2-x^2}$(cm).

Diện tích mặt cắt ngang của máng nước hay chính là diện tích hình thang cân ABCD là S = (AB + CD) ∙ AF : 2 = (a + 2x + a) ∙ $\sqrt{a^2-x^2}$: 2 = (a + x)$\sqrt{a^2-x^2}$ (cm²).

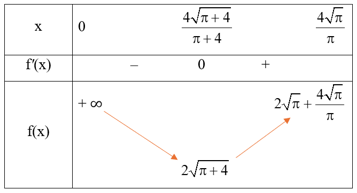
Xét hàm số S(x) = (a + x)$\sqrt{a^2-x^2}$ với x ∈ [0; a).

Ta có $S^{\text{'}}\left(x\right)=\sqrt{a^2-x^2}-\left(a+x\right)\frac{x}{\sqrt{a^2-x^2}}=\frac{-2x^2-ax+a^2}{\sqrt{a^2-x^2}}$.

S'(x) = 0 ⇔ – 2x² – ax + a² = 0 ⇔ (2x – a)(x + a) = 0 ⇔ x = $\frac{a}{2}$ ∈ [0; a).

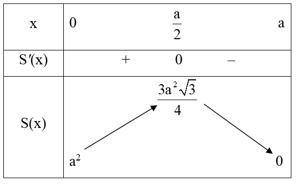
Bảng biến thiên:

Từ bảng biến thiên, ta có $\underset{\left[0;a\right)}{\max }S\left(x\right)=\frac{3a^2\sqrt{3}}{4}$, đạt được tại x = $\frac{a}{2}$.

Khi đó ta có, $\sin \widehat{DAF}=\frac{DF}{DA}=\frac{\frac{a}{2}}{a}=\frac{1}{2}\Rightarrow \widehat{DAF}=\frac{\pi }{6}$.

Suy ra $\widehat{DAB}=\widehat{DAF}+\widehat{FAB}=\frac{\pi }{6}+\frac{\pi }{2}=\frac{2\pi }{3}\in \left[\frac{\pi }{2};\pi \right)$.

Vậy $\alpha =\frac{2\pi }{3}$ thì diện tích mặt cắt ngang của máng lớn nhất.

2. Giải bài toán tối ưu trong kinh tế

Thực hành 3 trang 19 Chuyên đề Toán 12: Tại một xưởng sản xuất, chi phí để sản xuất x sản phẩm mỗi tháng là C(x) = 5 000 + 50x + 0,005x² (nghìn đồng).

a) Tính chi phí trung bình để sản xuất một sản phẩm.

b) Mỗi tháng xưởng sản xuất bao nhiêu sản phẩm thì chi phí trung bình để sản xuất một sản phẩm thấp nhất?

Lời giải:

a) Chi phí trung bình (nghìn đồng) để sản xuất một sản phẩm là

$\overline{C}\left(x\right)=\frac{C\left(x\right)}{x}=\frac{5000+50x+\mathrm{0,005}{x}^2}{x}=\frac{5000}{x}+50+\mathrm{0,005}x$ với x > 0.

b) Xét hàm số $\overline{C}\left(x\right)=\frac{5000}{x}+50+\mathrm{0,005}x$ với x ∈ (0; + ∞).

Ta có ${\overline{C}}^{\text{'}}\left(x\right)=\mathrm{0,005}-\frac{5000}{x^2}$;

${\overline{C}}^{\text{'}}\left(x\right)=0\iff \mathrm{0,005}-\frac{5000}{x^2}=0\iff x^2=1000000\iff x=1000\in \left(0;+\infty \right)$.

Ta có $\overline{C}\left(1000\right)=60$.

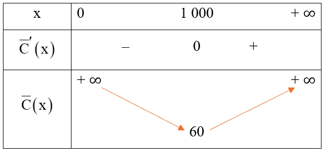
Bảng biến thiên:

Từ bảng biến thiên, ta thấy chi phí trung bình thấp nhất là $\overline{C}\left(1000\right)=60$(nghìn đồng/sản phẩm), đạt được khi x = 1 000 sản phẩm.

Vậy mỗi tháng xưởng sản xuất 1 000 sản phẩm thì chi phí trung bình để sản xuất một sản phẩm thấp nhất.

Thực hành 4 trang 20 Chuyên đề Toán 12: Cơ sở A chuyên cung cấp một loại sản phẩm nông nghiệp X cho nhà phân phối B. Hai bên thỏa thuận rằng, nếu đầu tháng B đặt hàng x tạ sản phẩm X thì giá bán mỗi tạ sản phẩm là P(x) = 5 – 0,0005x² (triệu đồng) (x ≤ 40). Chi phí A phải bỏ ra cho x tạ sản phẩm X trong một tháng là C(x) = 10 + 3,5x (triệu đồng).

a) Nếu trong một tháng A bán x tạ sản phẩm X cho B thì A nhận được bao nhiêu doanh thu, bao nhiêu lợi nhuận?

b) Trong một tháng B đặt hàng bao nhiêu tạ sản phẩm X từ A thì A nhận được lợi nhuận lớn nhất?

Lời giải:

a) Doanh thu mà A nhận được từ việc bán x tạ sản phẩm X (0 ≤ x ≤ 40) cho B là

R(x) = x ∙ P(x) = x(5 – 0,0005x²) = 5x – 0,0005x³ (triệu đồng).

Lợi nhuận (triệu đồng) mà A thu được là

L(x) = R(x) – C(x) = 5x – 0,0005x³ – (10 + 3,5x)

= – 0,0005x³ + 1,5x – 10 (0 ≤ x ≤ 40).

b) Xét hàm số f(x) = – 0,0005x³ + 1,5x – 10 với 0 ≤ x ≤ 40, ta có:

f'(x) = – 0,0015x² + 1,5;

f'(x) = 0 ⇔ – 0,0015x² + 1,5 = 0 ⇔ x² = 1 000 $\iff x=10\sqrt{10}\in \left[0;40\right]$.

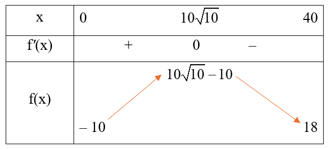
Ta có f(0) = – 10; $f\left(10\sqrt{10}\right)=10\sqrt{10}-10$; f(40) = 18.

Bảng biến thiên:

Từ bảng biến thiên, ta có $\underset{\left[0;40\right]}{\max }f\left(x\right)=10\sqrt{10}-10\approx \mathrm{21,623}$, đạt được khi $x=10\sqrt{10}\approx \mathrm{31,623}$.

Vậy trong một tháng B đặt hàng khoảng 31,623 tạ sản phẩm X từ A thì A nhận được lợi nhuận lớn nhất.

Vận dụng trang 20 Chuyên đề Toán 12: Hiện tại, mỗi tháng một cửa hàng đồ lưu niệm bán được 100 sản phẩm A. Với mỗi sản phẩm A bán được, cửa hàng thu được 20 nghìn đồng lợi nhuận. Qua khảo sát, người ta thấy rằng với mỗi nghìn đồng giảm giá, cửa hàng bán thêm được 10 sản phẩm A. Cửa hàng nên giảm giá bao nhiêu cho mỗi sản phẩm A để thu được lợi nhuận lớn nhất từ việc bán sản phẩm này? Tính lợi nhuận lớn nhất đó.

Lời giải:

Gọi x (nghìn đồng, x ≥ 0) là số tiền giảm giá cho mỗi sản phẩm A.

Với mỗi nghìn đồng giảm giá, cửa hàng bán thêm được 10 sản phẩm A nên với x nghìn đồng giảm giá, cửa hàng bán thêm được 10x sản phẩm A. Khi đó, mỗi tháng cửa hàng bán được số sản phẩm là 100 + 10x (sản phẩm).

Khi giảm giá x nghìn đồng cho mỗi sản phẩm A thì lợi nhuận trên mỗi sản phẩm A bán ra được lúc này là 20 – x (nghìn đồng).

Rõ ràng 20 – x ≥ 0, do đó x phải thỏa mãn điều kiện 0 ≤ x ≤ 20.

Lợi nhuận từ việc bán sản phẩm A của cửa hàng trong một tháng sau khi giảm giá là

L(x) = (100 + 10x) ∙ (20 – x) = 2 000 + 100x – 10x² (nghìn đồng).

Xét hàm số L(x) = 2 000 + 100x – 10x² với x ∈ [0; 20].

Ta có L'(x) = 100 – 20x;

L'(x) = 0 ⇔ 100 – 20x = 0 ⇔ x = 5 ∈ [0; 20].

Ta có L(0) = 2 000; L(5) = 2 250; L(20) = 0.

Suy ra $\underset{\left[0;20\right]}{\max }L\left(x\right)=2250$, đạt được tại x = 5.

Vậy cửa hàng nên giảm giá 5 nghìn đồng cho mỗi sản phẩm A để thu được lợi nhuận lớn nhất từ việc bán sản phẩm này là 2 triệu 250 nghìn đồng.

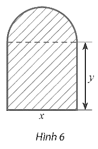
Bài 1 trang 20 Chuyên đề Toán 12: Người ta muốn xây một đường cống thoát nước có mặt cắt ngang là hình tạo bởi một nửa hình tròn ghép với một hình chữ nhật (Hình 6). Biết rằng mặt cắt ngang có diện tích 2 m². Các kích thước x, y (đơn vị: m) bằng bao nhiêu để chu vi của mặt cắt ngang là nhỏ nhất? Tính chu vi nhỏ nhất đó.

Lời giải:

Đường kính của nửa hình tròn là x (m, x > 0), suy ra bán kính nửa hình tròn là $\frac{x}{2}$(m).

Diện tích phần mặt cắt hình chữ nhật là S₁ = xy (m²). (x, y > 0)

Diện tích phần mặt cắt nửa hình tròn là S₂ = $\frac{1}{2}\pi {\left(\frac{x}{2}\right)}^2=\frac{1}{8}\pi x^2$ (m²).

Theo bài ra ta có S₁ + S₂ = 2 hay $xy+\frac{1}{8}\pi x^2=2$, suy ra $y=\frac{2}{x}-\frac{1}{8}\pi x$.

Vì x, y > 0 nên $\frac{2}{x}-\frac{1}{8}\pi x>0$, từ đó suy ra $0<x<\frac{4\sqrt{\pi }}{\pi }$.

Chu vi nửa hình tròn là C₁ = $\frac{1}{2}$πx (m).

Chu vi mặt cắt ngang là

C = $\frac{1}{2}\pi x+x+2y=\frac{1}{2}\pi x+x+2\left(\frac{2}{x}-\frac{1}{8}\pi x\right)=\frac{1}{4}\pi x+x+\frac{4}{x}$(m) với $0<x<\frac{4\sqrt{\pi }}{\pi }$.

Xét hàm số f(x) = $\frac{1}{4}\pi x+x+\frac{4}{x}$ với $0<x<\frac{4\sqrt{\pi }}{\pi }$.

Ta có $f^{\text{'}}\left(x\right)=\frac{1}{4}\pi +1-\frac{4}{x^2}$;

f'(x) = 0 $\iff \frac{1}{4}\pi +1-\frac{4}{x^2}=0\iff x=\frac{4\sqrt{\pi +4}}{\pi +4}\in \left(0;\frac{4\sqrt{\pi }}{\pi }\right)$.

Bảng biến thiên:

Từ bảng biến thiên, ta có $\underset{\left(0;\frac{4\sqrt{\pi }}{\pi }\right)}{\min }f\left(x\right)=2\sqrt{\pi +4}$, đạt được tại $x=\frac{4\sqrt{\pi +4}}{\pi +4}$.

Với $x=\frac{4\sqrt{\pi +4}}{\pi +4}$ thì $y=\frac{2}{x}-\frac{1}{8}\pi x=\frac{2\sqrt{\pi +4}}{\pi +4}$.

Vậy $x=\frac{4\sqrt{\pi +4}}{\pi +4}$ (m) và $y=\frac{2\sqrt{\pi +4}}{\pi +4}$(m) thì chu vi của mặt cắt ngang là nhỏ nhất và giá trị nhỏ nhất này bằng $2\sqrt{\pi +4}$(m).

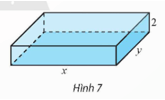
Bài 2 trang 20 Chuyên đề Toán 12: Người ta muốn xây một bể bơi có dạng hình hộp chữ nhật, thể tích 1 800 m³ và chiều sâu 2 m (Hình 7). Biết rằng chi phí xây mỗi đơn vị diện tích của đáy bể gấp hai lần so với thành bể. Cần chọn chiều dài và chiều rộng của bể bằng bao nhiêu để tiết kiệm chi phí xây dựng bể nhất?

Lời giải:

Gọi x, y (x > 0, y > 0, tính bằng mét) lần lượt là chiều dài và chiều rộng của bể.

Thể tích của bể là V = 2xy = 1 800 (m³), suy ra $y=\frac{900}{x}$(m).

Diện tích đáy bể là S_đ = xy (m²).

Diện tích thành bể là S_t = 2(x + y) ∙ 2 = 4(x + y) (m²).

Giả sử chi phí để xây mỗi đơn vị diện tích thành bể là a (đồng, a > 0).

Khi đó chi phí để xây mỗi đơn vị diện tích đáy bể là 2a (đồng).

Tổng chi phí để xây bể bơi là

C = 2axy + a ∙ 4(x + y) = $2ax\cdot \frac{900}{x}+4a\left(x+\frac{900}{x}\right)=1800a+4ax+\frac{3600a}{x}$(đồng).

Xét hàm số f(x) = 1800a + 4ax + $\frac{3600a}{x}$ với x ∈ (0; + ∞) và a > 0.

Ta có f'(x) = 4a – $\frac{3600a}{x^2}$;

f'(x) = 0 ⇔ $4a-\frac{3600a}{x^2}=0\iff x^2=900\iff x=30\in \left(0;+\infty \right)$.

Bảng biến thiên:

Từ bảng biến thiên, ta có $\underset{\left(0;+\infty \right)}{\min }f\left(x\right)=2040a$, đạt được tại x = 30.

Với x = 30 m thì ta có $y=\frac{900}{x}=\frac{900}{30}=30$.

Vậy với chiều rộng và chiều dài của bể bằng nhau và bằng 30 m thì tiết kiệm được chi phí xây dựng bể nhất.

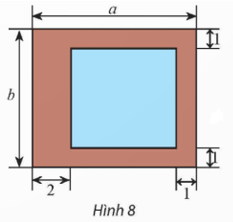
Bài 3 trang 20 Chuyên đề Toán 12: Người ta muốn thiết kế một lồng nuôi cá có bề mặt hình chữ nhật bao gồm phần mặt nước có diện tích bằng 54 m² và phần đường đi xung quanh với kích thước (đơn vị: m) như Hình 8. Bề mặt của lồng có chiều dài và chiều rộng bằng bao nhiêu để diện tích phần đường đi là bé nhất?

Lời giải:

Từ hình vẽ, ta tính được kích thước hình chữ nhật phần mặt nước là a – 3 (m) và b – 2 (m). Từ đó suy ra a > 3 và b > 2.

Diện tích phần mặt nước là S₁ = (a – 3)(b – 2) = 54 (m²)

Suy ra $b=\frac{54}{a-3}+2$(m).

Diện tích phần đường đi là S = ab – 54 = $a\cdot \left(\frac{54}{a-3}+2\right)-54=\frac{54a}{a-3}+2a-54$(m²).

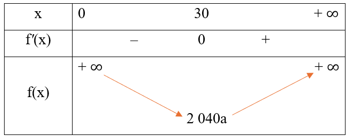
Xét hàm số $S\left(a\right)=\frac{54a}{a-3}+2a-54$ với a ∈ (3; + ∞).

Ta có $S^{\text{'}}\left(a\right)=2-\frac{162}{{\left(a-3\right)}^2}$;

S'(a) = 0 $\iff 2-\frac{162}{{\left(a-3\right)}^2}=0\iff {\left(a-3\right)}^2=81\iff a=12\in \left(3;+\infty \right)$.

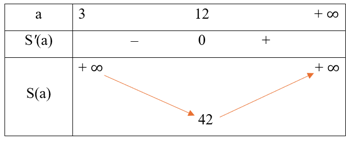
Bảng biến thiên:

Từ bảng biến thiên, ta có $\underset{\left(3;+\infty \right)}{\min }S\left(a\right)=42$, đạt được khi a = 12.

Với a = 12 thì ta có $b=\frac{54}{12-3}+2=8$.

Vậy bề mặt của lồng có chiều dài và chiều rộng lần lượt là 12 m và 8 m thì diện tích phần đường đi là bé nhất.

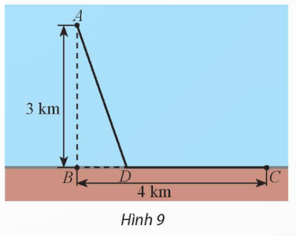
Bài 4 trang 21 Chuyên đề Toán 12: Một giếng dầu ngoài khơi được đặt ở vị trí A cách bờ biển 3 km, B là vị trí trên bờ biển gần giếng dầu nhất. Nhà máy lọc dầu được đặt ở vị trí C trên bờ biển, cách vị trí B một khoảng 4 km (Hình 9). Người ta dự định lắp đặt đường ống dẫn dầu gồm hai đoạn thẳng AD và DC (D là một vị trí nằm giữa B và C). Biết rằng mỗi mét đường ống đặt dưới biển có chi phí lắp đặt cao gấp đôi so với mỗi mét đường ống đặt trên bờ. Vị trí của D như thế nào để giảm thiểu chi phí lắp đặt nhất?

Lời giải:

Đặt BD = x (km, 0 ≤ x ≤ 4).

Ta có DC = 4 – x (km).

Áp dụng định lí Pythagore trong tam giác vuông ABD, ta có:

AD = $\sqrt{x^2+3^2}=\sqrt{x^2+9}$(km).

Giả sử chi phí lắp đặt mỗi mét đường ống dẫn dầu trên bờ là a (đồng, a > 0).

Khi đó chi phí lắp đặt mỗi mét đường ống dẫn dầu đặt dưới biển là 2a (đồng).

Tổng chi phí lắp đặt đường ống là

C = 2a$\sqrt{x^2+9}$ + a(4 – x) = 2a$\sqrt{x^2+9}$ + 4a – ax (đồng).

Xét hàm số f(x) = 2a$\sqrt{x^2+9}$ + 4a – ax với x ∈ [0; 4] và a > 0.

Ta có f'(x) = $\frac{2ax}{\sqrt{x^2+9}}-a$;

f'(x) = 0 $\iff \frac{2ax}{\sqrt{x^2+9}}-a=0\iff \sqrt{x^2+9}=2x$

⇔ x² + 9 = 4x² ⇔ 3x² = 9 ⇔ x² = 3 ⇔ x = $\sqrt{3}$ ∈ [0; 4].

Ta có f(0) = 10a; $f\left(\sqrt{3}\right)=\left(3\sqrt{3}+4\right)a$; f(4) = 10a.

Do đó, $\underset{\left[0;4\right]}{\min }f\left(x\right)=f\left(\sqrt{3}\right)=\left(3\sqrt{3}+4\right)a$(do a > 0) tại x = $\sqrt{3}$.

Vậy cần đặt vị trí D nằm giữa B và C sao cho D cách B một khoảng bằng $\sqrt{3}$km để giảm thiểu chi phí lắp đặt nhất.

Bài 5 trang 21 Chuyên đề Toán 12: Tại một xí nghiệp, nếu trong một tuần xí nghiệp sản xuất x nghìn sản phẩm thì chi phí sản xuất gồm: 10 triệu đồng chi phí cố định, 3 triệu đồng cho mỗi nghìn sản phẩm và 0,001x² triệu đồng chi phí bảo dưỡng thiết bị.

a) Tính chi phí trung bình trên mỗi nghìn sản phẩm theo x.

b) Mỗi tuần xí nghiệp cần sản xuất bao nhiêu sản phẩm để chi phí trung bình thấp nhất?

Lời giải:

a) Chi phí để xí nghiệp sản xuất x nghìn sản phẩm trong một tuần là

C(x) = 10 + 3x + 0,001x² (triệu đồng) với x ≥ 0.

Chi phí trung bình (triệu đồng) để sản xuất mỗi nghìn sản phẩm là

$\overline{C}\left(x\right)=\frac{C\left(x\right)}{x}=\frac{10+3x+\mathrm{0,001}{x}^2}{x}=\frac{10}{x}+3+\mathrm{0,001}x$ với x > 0.

b) Ta có ${\overline{C}}^{\text{'}}\left(x\right)=\mathrm{0,001}-\frac{10}{x^2}$;

${\overline{C}}^{\text{'}}\left(x\right)=0\iff \mathrm{0,001}-\frac{10}{x^2}=0\iff x^2=10000\iff x=100\in \left(0;+\infty \right)$.

Ta có $\overline{C}\left(100\right)=\frac{16}{5}=\mathrm{3,2}$.

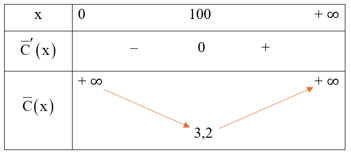
Bảng biến thiên:

Từ bảng biến thiên ta thấy chi phí trung bình thấp nhất là $\overline{C}\left(100\right)=\mathrm{3,2}$(triệu đồng/nghìn sản phẩm), đạt được khi x = 100 (nghìn sản phẩm).

Vậy mỗi tuần xí nghiệp cần sản xuất 100 nghìn sản phẩm để chi phí trung bình thấp nhất.