Chuyên đề Toán 12 Bài 1 (Chân trời sáng tạo): Tiền tệ. Lãi suất

Giải Chuyên đề Toán 12 Bài 1: Tiền tệ. Lãi suất

Khởi động trang 25 Chuyên đề Toán 12: Tại sao con người lại phát minh ra tiền? Hãy nêu những khó khăn trong đời sống khi con người chưa phát minh ra tiền giấy.

Lời giải:

– Khi lực lượng sản xuất và phân công lao động xã hội phát triển, sản xuất hàng hóa và thị trường ngày càng mở rộng thì tình trạng có nhiều vật ngang giá chung làm cho trao đổi giữa các điạ phương vấp phải khó khăn, do đó đòi hỏi khách quan phải hình thành vật ngang giá chung thống nhất. Khi vật ngang giá chung được cố định ở một hàng hóa độc tôn và phổ biến thì xuất hiện hình thái tiền tệ của giá trị.

– Trước khi tiền giấy xuất hiện, con người sử dụng tiền kim loại (đồng xu vàng và bạc) để trao đổi. Những khó khăn trong đời sống khi con người chưa phát minh ra tiền giấy:

⦁ Tiền kim loại nặng, dễ rơi mất, khó bảo quản;

⦁ Những thương nhân mua bán khối lượng hàng hóa lớn nếu thanh toán bằng tiền vàng thì việc vận chuyển vàng trở nên rất nặng nề;

⦁ Những thương nhân mua bán trong phạm vi rộng, thậm chí xuyên quốc gia, nếu sử dụng tiền vàng trong thanh toán thì việc bảo quản và vận chuyển tiền, tránh nạn cướp bóc trên đường đi, trở thành một gánh nặng lớn;

Khám phá 1 trang 25 Chuyên đề Toán 12: a) Hằng ngày bạn dùng tiền để làm gì?

b) Kể tên các hình thức của tiền từ xưa đến nay mà bạn biết.

c) Đơn vị tiền tệ của mỗi nước có giống nhau không?

Lời giải:

a) Hằng ngày em dùng tiền để trả tiền xe bus, mua sắm hàng hóa như: bánh mì, sữa, hoa quả, …

b) Các hình thức của tiền từ xưa đến nay mà em biết: hóa tệ không kim (vỏ ốc, vỏ sò, da thú, …); hóa tệ bằng kim (vật được làm bằng đồng, bạc, vàng, thỏi bạc, thỏi vàng); tiền kim loại (tiền xu); tiền giấy; tiền trong tài khoản ngân hàng; tiền tệ điện tử (Visa card, credit card, payment card).

c) Đơn vị tiền tệ của mỗi nước không giống nhau. Chẳng hạn:

⦁ Đồng (VND) là tiền tệ của Việt Nam;

⦁ Đô la Singapore (SGD) là tiền tệ của Singapore;

⦁ Baht (THB) là tiền tệ của Thái Lan;

⦁ Đô la Mỹ (USD) là tiền tệ của Mỹ;

⦁ Đồng Euro (EUR) là đồng tiền chung của liên minh châu Âu (EU), là tiền tệ của 20 quốc gia: Đức, Áo, Bỉ, Bồ Đào Nha, Pháp, …

Thực hành 1 trang 26 Chuyên đề Toán 12: Kể tên đơn vị tiền tệ của các nước: Anh, Úc, Nhật Bản, Hàn Quốc, Malaysia (theo Ngân hàng Nhà nước Việt Nam).

Lời giải:

Theo Ngân hàng Nhà nước Việt Nam, ta có:

Vận dụng 1 trang 26 Chuyên đề Toán 12: Kể tên bốn nước dùng chung đơn vị tiền tệ là đồng Euro.

Lời giải:

Bốn nước dùng chung đơn vị tiền tệ là đồng Euro: Đức, Pháp, Hà Lan, Bồ Đào Nha.

Khám phá 2 trang 26 Chuyên đề Toán 12: a) Làm thế nào để quy đổi tiền của nước này sang tiền của nước khác?

b) Em hãy tìm hiểu một số thông tin trong bảng ở Hình 2.

Lời giải:

a) Để quy đổi tiền của nước này sang tiền của nước khác ta dựa trên tỉ giá giữa hai loại tiền tệ (tỉ giá).

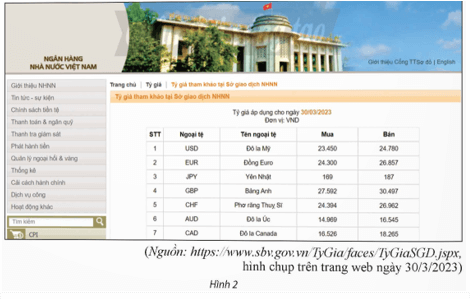
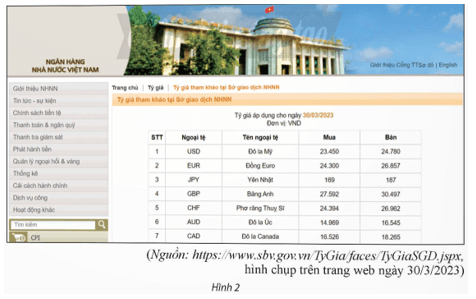
b) Bảng trong Hình 2 cho biết:

⦁ Một số tên ngoại tệ và kí hiệu đơn vị ngoại tệ;

⦁ Giá mua và bán của các ngoại tệ (USD, EUR, JPY, GBP, CHF, AUD, CAD) đối với đơn vị tiền tệ VND của Sở giao dịch Ngân hàng Nhà nước Việt Nam vào ngày 30/3/2023.

Thực hành 2 trang 27 Chuyên đề Toán 12: Sử dụng Bảng tỉ giá ở Hình 2 để trả lời câu hỏi sau:

a) Bà Lan mua 250 EUR từ ngân hàng vào ngày 30/3/2023. Hỏi bà Lan phải trả bao nhiêu VND?

b) Anh Tuấn bán 3 500 EUR cho ngân hàng vào ngày 30/3/2023. Hỏi anh Tuấn thu được bao nhiêu VND?

Lời giải:

a) Bà Lan mua 250 EUR từ ngân hàng vào ngày 30/3/2023 nên ngân hàng sẽ áp dụng tỉ giá bán cho bà Lan. Vậy bà Lan cần trả: 250 . 26 857 = 6 714 250 (VND).

b) Anh Tuấn bán 3 500 EUR cho ngân hàng vào ngày 30/3/2023 nên ngân hàng sẽ áp dụng tỉ giá mua để quy đổi. Vậy anh Tuấn sẽ thu được: 3 500 . 24 300 = 85 050 000 (VND).

Vận dụng 2 trang 27 Chuyên đề Toán 12: Truy cập trang web https:/www.sbv.gov.vn/lyGia/faces/1yCia.jspx của Ngân hàng Nhà nước Việt Nam để xem tỉ giá trao đổi ngoại tệ trong ngày.

a) Xác định giá mua 1 000 GBP (bảng Anh) từ ngân hàng.

b) Xác định giá bán 15 000 JPY (yên Nhật) cho ngân hàng.

c) Xác định giá mua 20 000 AUD (đô la Úc) từ ngân hàng.

Lời giải:

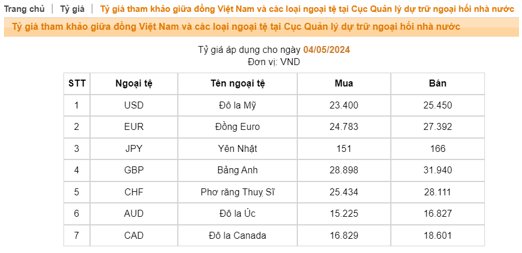
Truy cập trang web https:/www.sbv.gov.vn/lyGia/faces/1yCia.jspx của Ngân hàng Nhà nước Việt Nam ta có tỉ giá trao đổi ngoại tệ trong ngày 4/5/2024 như sau:

a) Cần mua GBP (bảng Anh) từ ngân hàng nên ngân hàng sẽ áp dụng tỉ giá bán là mua 1 GBP phải trả 31 940 VND.

Vậy giá mua 1 000 GBP (bảng Anh) từ ngân hàng là:

1 000 . 31 940 = 31 940 000 (VND).

b) Cần bán JPY (yên Nhật) cho ngân hàng nên ngân hàng sẽ áp dụng tỉ giá mua là bán 1 JPY thu được 151 VND.

Vậy giá bán 15 000 JPY (yên Nhật) cho ngân hàng là:

15 000 . 151 = 2 265 000 (VND).

c) Cần mua AUD (đô la Úc) từ ngân hàng nên ngân hàng sẽ áp dụng tỉ giá bán là mua 1 AUD phải trả 16 827 VND.

Vậy giá mua 20 000 AUD (đô la Úc) từ ngân hàng là:

20 000 . 16 827 = 336 540 000 (VND).

Khám phá 3 trang 27 Chuyên đề Toán 12: Đầu năm ông A đã vay của ông B 100 triệu đồng, hai bên thoả thuận đến cuối năm ông A phải hoàn trả cho ông B 100 triệu đồng tiền vốn đã vay và trả thêm 8 triệu đồng tiền lãi. Tìm tỉ số phần trăm giữa tiền lãi và tiền vốn.

Lời giải:

Tỉ số phần trăm giữa tiền lãi và tiền vốn là: $\frac{8}{100}\cdot 100\%=8\%.$

Khám phá 4 trang 28 Chuyên đề Toán 12: Một người gửi tiết kiệm 100 triệu đồng vào ngân hàng. So sánh số tiền lãi mà người đó nhận được sau 4 năm (kì hạn một nǎm) trong hai trường hợp sau:

Trường hợp 1. Lãi suất 8%/năm. Tiền lãi không được nhập vào vốn sau mỗi năm tính lãi của khoản vay.

Trường hợp 2. Lãi suất 7,5%/năm. Tiền lãi được nhập vào vốn sau mỗi năm để tính lãi cho năm kế tiếp của khoản vay.

Lời giải:

Trường hợp 1.

Tiền lãi người đó nhận được sau 1 năm là: 100.8% = 8 (triệu đồng).

Tiền lãi người đó nhận được sau 4 năm là: 4.8 = 32 (triệu đồng).

Trường hợp 2.

Tiền lãi người đó nhận được sau kì hạn năm thứ nhất là:

100. 7,5% = 7,5 (triệu đồng).

Tiền lãi người đó nhận được sau kì hạn năm thứ hai là:

(100 + 7,5).7,5% = 8,0625 (triệu đồng).

Tiền lãi người đó nhận được sau kì hạn năm thứ ba là:

(100 + 7,5 + 8,0625).7,5% = 8,6671 (triệu đồng).

Tiền lãi người đó nhận được sau kì hạn năm thứ tư là:

(100 + 7,5 + 8,0625 + 8,6671).7,5% = 9,31722 (triệu đồng).

Vậy sau 4 năm, người đó nhận được số tiền lãi là:

7,5 + 8,0625 + 8,6671 + 9,31722 = 33,54682 (triệu đồng).

Vậy số tiền lãi mà người đó nhận được sau 4 năm (kì hạn một nǎm) trong trường hợp 2 nhiều hơn trường hợp 1.

Thực hành 3 trang 29 Chuyên đề Toán 12: Cho vay với vốn gốc 250 triệu đồng, lãi suất 12%/năm, kì trả lãi 6 tháng, kì hạn vay 4 năm. Tính tiền lãi sau 4 năm theo phương thức tính:

a) Lãi đơn;

b) Lãi kép.

Lời giải:

Ta có P = 250 (triệu đồng); $r=\frac{6}{12}\cdot 12\%=6\%;$$n=\frac{4\cdot 12}{6}=8.$

a) Tiền lãi tính theo phương thức lãi đơn là:

I_n = P.r.n = 250 . 6% . 8 = 120 (triệu đồng).

b) Tiền lãi tính theo phương thức tính lãi kép là:

$I_n=P\left[{\left(1+r\right)}^n-1\right]=250\cdot \left[{\left(1+6\%\right)}^8-1\right]\approx \mathrm{148,462}$ (triệu đồng).

Vận dụng 3 trang 29 Chuyên đề Toán 12: Bác Tư gửi 400 triệu đồng vào ngân hàng A với lãi suất 4,8%/năm, kì trả lãi 3 tháng. Nếu rút trước kì hạn thì ngân hàng sẽ tính theo lãi suất không kì hạn là 0,1%/năm cho số ngày gửi thêm (tính lãi theo ngày). Tính tổng số tiền cả vốn và lãi bác Tư nhận được sau 290 ngày gửi tiền vào ngân hàng A (lãi suất không đổi suốt kì gửi tiền) theo phương thức tính:

a) Lãi đơn;

b) Lãi kép.

Lời giải:

Giả sử mỗi tháng đều có 30 ngày, khi đó nếu bác Tư rút tiền sau 290 ngày gửi tiết kiệm thì bác Tư đã nhận được 3 kì trả lãi (9 tháng tức 270 ngày) và số ngày gửi thêm là 20 ngày.

Ta có P = 400 (triệu đồng); $r=\frac{3}{12}\cdot \mathrm{4,8}\%=\mathrm{1,2}\%;$ n = 3.

a) Tiền lãi cho 3 kì trả lãi tính theo phương thức tính lãi đơn là:

I_n = P.r.n = 400 . 1,2% . 3 = 14,4 (triệu đồng).

Tiền lãi cho 20 ngày gửi thêm là:

${I_n}^{\text{'}}=400\cdot \frac{20}{365}\cdot \mathrm{0,1}\%\approx \mathrm{0,0219}$ (triệu đồng).

Vậy tổng số tiền cả vốn và lãi bác Tư nhận được sau 290 ngày gửi tiền vào ngân hàng A theo phương thức tính lãi đơn khoảng:

400 + 14,4 + 0,0219 = 414,4219 (triệu đồng).

b) Tiền lãi cho 3 kì trả lãi tính theo phương thức tính lãi kép là:

$I_n=P\left[{\left(1+r\right)}^n-1\right]=400\left[{\left(1+\mathrm{1,2}\%\right)}^3-1\right]\approx \mathrm{14,573}$ (triệu đồng).

Tiền lãi cho 20 ngày gửi thêm là:

${I_n}^{\text{'}}\approx \left(400+\mathrm{14,573}\right)\cdot \frac{20}{365}\cdot \mathrm{0,1}\%\approx \mathrm{0,0227}$ (triệu đồng).

Vậy tổng số tiền cả vốn và lãi bác Tư nhận được sau 290 ngày gửi tiền vào ngân hàng A theo phương thức tính lãi kép khoảng:

400 + 14,573 + 0,0227 = 414,5957 (triệu đồng).

Khám phá 5 trang 29 Chuyên đề Toán 12: Bạn Minh hay đi chợ giúp mẹ. Minh nhận thấy 1 kg thịt bò hôm nay có giá 280 nghìn đồng trong khi cách đây một năm 1 kg thịt bò đó chỉ có giá 250 nghìn đồng.

a) So với năm ngoái, giá một cân thịt bò đã tăng bao nhiêu phần trăm?

b) Theo em, sự tăng giá của giá cả hàng hoá nói lên điều gì về giá trị đồng tiền?

Lời giải:

a) So với năm ngoái, giá một cân thịt bò đã tăng số phần trăm là:

$\frac{280-250}{250}\cdot 100\%=12\%.$

b) Theo em, sự tăng giá của giá cả hàng hoá nói lên sự lạm phát về giá trị đồng tiền.

Khám phá 6 trang 30 Chuyên đề Toán 12: Giả sử tỉ lệ lạm phát của năm 2023 so với năm 2022 là 10%. Hãy cho biết:

a) 1 triệu đồng năm 2023 có giá trị tương đương với bao nhiêu tiền vào năm 2022.

b) 1 triệu đồng năm 2022 có giá trị tương đương với bao nhiêu tiền vào năm 2023.

Lời giải:

a) Gọi x là số tiền tương đương ở năm 2022.

Khi đó, ta có: $\frac{1-x}{x}\cdot 100\%=10\%,$ do đó 1 – x = 0,1x, suy ra x ≈ 0,909 (triệu đồng).

Vậy 1 triệu đồng năm 2023 có giá trị tương đương với 0,909 triệu đồng (909 nghìn đồng) ở năm 2022.

b) Gọi x là số tiền tương đương ở năm 2023.

Khi đó, ta có: $\frac{1-x}{x}\cdot 100\%=10\%,$ do đó x = 1,1 (triệu đồng).

Vậy 1 triệu đồng năm 2022 có giá trị tương đương với 1,1 triệu đồng ở năm 2023.

Thực hành 4 trang 30 Chuyên đề Toán 12: Giả sử tỉ lệ lạm phát của năm 2022 so với năm 2021 là 5%. Hãy cho biết:

a) 50 triệu đồng năm 2022 có giá trị tương đương với bao nhiêu tiền vào năm 2021.

b) 50 triệu đồng năm 2021 có giá trị tương đương với bao nhiêu tiền vào năm 2022.

Lời giải:

a) Ta có $\frac{1}{1+5\%}\cdot 50\approx \mathrm{47,619}$ (triệu đồng).

Vậy 50 triệu đồng năm 2022 có giá trị tương đương với khoảng 47,619 triệu đồng ở năm 2021.

b) Ta có (1 + 5%) . 50 = 52,5 (triệu đồng).

Vậy 50 triệu đồng năm 2021 có giá trị tương đương với 52,5 triệu đồng ở năm 2022.

Vận dụng 4 trang 30 Chuyên đề Toán 12: Giả sử tỉ lệ lạm phát của năm 2012 so với năm 2011 là 16,7% và tỉ lệ lạm phát năm 2013 so với năm 2012 là 7,1%. Cho biết giá của một ổ bánh mì cuối năm 2011 là 2 000 đồng và giá bánh mì gia tăng theo lạm phát thì giá một ổ bánh mì năm 2013 sẽ là bao nhiêu? (Làm tròn kết quả đến hàng trăm.)

Lời giải:

Ta có: (1 + 16,7%).2000 = 2 334 (đồng).

Do đó 2 000 đồng năm 2011 có giá trị tương đương với 2 334 đồng ở năm 2012.

Ta có: (1 + 7,1%).2 334 = 2 497,38 (đồng) ≈ 2 500 (đồng).

Do đó 2 334 đồng năm 2012 có giá trị tương đương với 2 500 đồng ở năm 2013.

Vậy giá một ổ bánh mì năm 2013 là 2 500 đồng.

Khám phá 7 trang 31 Chuyên đề Toán 12: Ngày 01/6/2021, ông An gửi 100 triệu đồng vào ngân hàng với lãi suất năm là R = 10% (kì hạn một năm).

a) Đến ngày 01/6/2022 ông An rút tiền ra thì tổng số tiền cả vốn và lãi là bao nhiêu?

b) Cho biết từ 01/6/2021 đến 01/6/2022 tỉ lệ lạm phát là i = 2%. Hỏi số tiền ông An nhận được tương đương với bao nhiêu tiền vào thời điểm 01/6/2021?

c) Tính lãi suất thực tế r nếu có tính thêm yếu tố lạm phát.

Lời giải:

a) Ông An gửi tiết kiệm từ ngày 01/6/2021 và đến ngày 01/6/2022 thì rút tiền, tức ông An đã gửi tiết kiệm được 1 năm.

Vậy tổng số tiền cả vốn và lãi ông An nhận được là:

100 . (1 + 10%) = 110 (triệu đồng).

b) Ta có: $\frac{1}{1+2\%}\cdot 110\approx \mathrm{107,843}$(triệu đồng).

Vậy số tiền ông An nhận được tương đương với khoảng 107,843 triệu đồng ở thời điểm 01/6/2021.

c) Lãi suất thực tế nếu có tính thêm yếu tố lạm phát là:

$r=\frac{\mathrm{107,843}-100}{100}\cdot 100\%=\mathrm{7,843}\%.$

Thực hành 5 trang 31 Chuyên đề Toán 12: Ba của Lan gửi tiết kiệm vào ngân hàng với lãi suất được ngân hàng niêm yết là 12%/năm (kì hạn một năm). Cho biết trong năm đó tỉ lệ lạm phát là 4%. Tính lãi suất danh nghĩa và lãi suất thực.

Lời giải:

Lãi suất danh nghĩa là R = 12%, tỉ lệ lạm phát là i = 4%.

Lãi suất thực là: $r=\frac{1+R}{1+i}-1=\frac{1+12\%}{1+4\%}-1\approx \mathrm{7,69}\%.$

Vận dụng 5 trang 31 Chuyên đề Toán 12: Theo Tổng cục Thống kê năm 2021, tỉ lệ lạm phát của Việt Nam là 1,84% (nguồn: www.gso.gov.vn). Ông Đạt gửi tiết kiệm trong năm 2021 với lãi suất 6%/năm, kì hạn một năm. Tính lãi suất danh nghĩa và lãi suất thực.

Lời giải:

Lãi suất danh nghĩa là R = 6%, tỉ lệ lạm phát là i = 1,84%.

Lãi suất thực là: $r=\frac{1+R}{1+i}-1=\frac{1+6\%}{1+\mathrm{1,84}\%}-1\approx \mathrm{4,08}\%.$

Bài tập

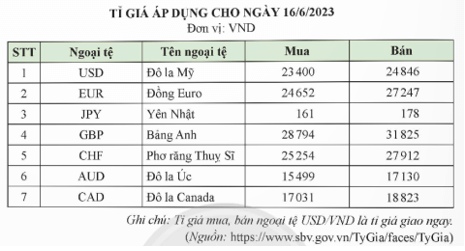
Bài 1 trang 32 Chuyên đề Toán 12: Dưới đây là bảng tỉ giá trao đổi ngoại tệ và VND tại Ngân hàng Nhà nước Việt Nam ngày 16/6/2023.

Áp dụng bảng tỉ giá trên để:

a) Quy đổi 1 500 JPY sang VND theo giá mua vào.

b) Quy đổi 750 AUD sang VND theo giá bán ra.

Lời giải:

a) Cần mua JPY (Yên Nhật) từ ngân hàng nên ngân hàng sẽ áp dụng tỉ giá bán là mua 1 JPY phải trả 178 VND.

Vậy giá mua 1 500 JPY (Yên Nhật) từ ngân hàng là:

1 500 . 178 = 267 000 (VND).

b) Cần bán AUD (đô la Úc) cho ngân hàng nên ngân hàng sẽ áp dụng tỉ giá mua là bán 1 AUD thu được 15 499 VND.

Vậy giá bán 750 AUD (đô la Úc) cho ngân hàng là:

750 . 15 499 = 11 624 250 (VND).

Bài 2 trang 32 Chuyên đề Toán 12: Ông Dũng cho vay 800 triệu đồng với lãi suất 9%/năm, kì trả lãi 6 tháng. Tính số tiền lãi ông Dũng nhận được sau 2 năm theo phương thức tính:

a) Lãi đơn;

b) Lãi kép.

Lời giải:

Ta có P = 800 (triệu đồng); $r=\frac{6}{12}\cdot 9\%=\mathrm{4,5}\%;$ $n=\frac{2\cdot 12}{6}=4.$

a) Tiền lãi ông Dũng nhận được tính theo phương thức tính lãi đơn là:

I_n = P.r.n = 800 . 4,5% . 4 = 144 (triệu đồng).

b) Tiền lãi ông Dũng nhận được tính theo phương thức tính lãi kép là:

$I_n=P\left[{\left(1+r\right)}^n-1\right]=800\cdot \left[{\left(1+\mathrm{4,5}\%\right)}^4-1\right]\approx \mathrm{154,015}$ (triệu đồng).

Bài 3 trang 32 Chuyên đề Toán 12: Bà Hương gửi 600 triệu đồng vào ngân hàng B với lãi suất 6,3%/ năm, kì hạn 3 tháng. Nếu rút trước kì hạn thì ngân hàng sẽ tính theo lãi suất không kì hạn là 0,2%/năm cho số ngày gửi thêm. Tính tổng số tiền cả vốn và lãi bà Hương nhận được sau 370 ngày gửi tiền vào ngân hàng B theo phương thức tính:

a) Lãi đơn;

b) Lãi kép.

Lời giải:

Nếu bà Hương rút tiền sau 370 ngày gửi tiết kiệm thì bà Hương đã nhận được 4 kì trả lãi (12 tháng tức 1 năm (365 ngày)) và số ngày gửi thêm là 5 ngày.

Ta có P = 600 (triệu đồng); $r=\frac{3}{12}\cdot \mathrm{6,3}\%=\mathrm{1,575}\%;$ n = 4.

a) Tiền lãi cho 4 kì trả lãi tính theo phương thức tính lãi đơn là:

I_n = P.r.n = 600 . 1,575% . 4 = 37,8 (triệu đồng).

Tiền lãi cho 5 ngày gửi thêm là:

${I_n}^{\text{'}}=600\cdot \frac{5}{365}\cdot \mathrm{0,2}\%\approx \mathrm{0,0164}$ (triệu đồng).

Vậy tổng số tiền cả vốn và lãi bà Hương nhận được sau 370 ngày gửi tiền vào ngân hàng B theo phương thức tính lãi đơn khoảng:

600 + 37,8 + 0,0164 = 637,8164 (triệu đồng).

b) Tiền lãi cho 4 kì trả lãi tính theo phương thức tính lãi kép là:

$I_n=P\left[{\left(1+r\right)}^n-1\right]=600\left[{\left(1+\mathrm{1,575}\%\right)}^4-1\right]\approx \mathrm{38,702}$ (triệu đồng).

Tiền lãi cho 5 ngày gửi thêm là:

${I_n}^{\text{'}}\approx \left(600+\mathrm{38,702}\right)\cdot \frac{5}{365}\cdot \mathrm{0,2}\%\approx \mathrm{0,0175}$ (triệu đồng).

Vậy tổng số tiền cả vốn và lãi bà Hương nhận được sau 370 ngày gửi tiền vào ngân hàng B theo phương thức tính lãi kép khoảng:

600 + 38,702 + 0,0175 = 638,7195 (triệu đồng).

Bài 4 trang 32 Chuyên đề Toán 12: Nếu tỉ lệ lạm phát hằng năm là 4% thì bao nhiêu năm nữa 1 tỉ đồng chỉ còn một nửa giá trị.

Lời giải:

Với tỉ lệ lạm phát hằng năm là 4%, thì:

⦁ Sau 1 năm, giá trị của 1 tỉ đồng là: 1.(1 – 4%) = (1 – 4%) (tỉ đồng);

⦁ Sau 2 năm, giá trị của 1 tỉ đồng là: (1 – 4%).(1 – 4%) = (1 – 4%)² (tỉ đồng);

⦁ Sau 3 năm, giá trị của 1 tỉ đồng là: (1 – 4%)².(1 – 4%) = (1 – 4%)³ (tỉ đồng);

…

⦁ Sau n năm, giá trị của 1 tỉ đồng là: (1 – 4%)ⁿ (tỉ đồng).

Theo bài, sau n năm thì nữa 1 tỉ đồng chỉ còn một nửa giá trị (tức 0,5 tỉ đồng) nên ta có:

(1 – 4%)ⁿ = 0,5

0,96ⁿ = 0,5

$n={\log }_{\mathrm{0,96}}\mathrm{0,5}\approx 17.$

Vậy nếu tỉ lệ lạm phát hằng năm là 4% thì 17 năm nữa 1 tỉ đồng chỉ còn một nửa giá trị.

Bài 5 trang 32 Chuyên đề Toán 12: Ông Long gửi tiền vào ngân hàng B với lãi suất thoả thuận là 9%/năm. Cho biết trong năm đó tỉ lệ lạm phát là 3%, tính lãi suất danh nghĩa và lãi suất thực.

Lời giải:

Lãi suất danh nghĩa là R = 9%, tỉ lệ lạm phát là i = 3%.

Lãi suất thực là: $r=\frac{1+R}{1+i}-1=\frac{1+9\%}{1+3\%}-1\approx \mathrm{5,825}\%.$