Chuyên đề Toán 12 Bài 1 (Chân trời sáng tạo): Bài toán quy hoạch tuyến tính

Giải Chuyên đề Toán 12 Bài 1: Bài toán quy hoạch tuyến tính

Khởi động trang 6 Chuyên đề Toán 12: Một thương nhân sử dụng 120 triệu đồng tiền vốn để mua tối đa 8 tấn trái cây. Thương nhân đó thu mua hai loại trái cây là A với giá 12 triệu đồng/tấn và B với giá 20 triệu đồng/tấn. Lợi nhuận thương nhân đó thu được sau khi bán mỗi tấn hàng đối với loại A là 1,1 triệu đồng, đối với loại B là 1,5 triệu đồng. Thương nhân đó nên mua khối lượng bao nhiêu mỗi loại để thu được lợi nhuận cao nhất khi bán hết hàng đã thu mua?

Lời giải:

Sau bài học, ta giải quyết được bài toán trên như sau:

Gọi x, y (tính theo tấn) lần lượt là khối lượng trái cây loại A và B được thương nhân thu mua, ta có x ≥ 0 và y ≥ 0.

Thương nhân mua tối đa 8 tấn trái cây nên x + y ≤ 8.

Số tiền mua x tấn trái cây loại A là 12x (triệu đồng).

Số tiền mua y tấn trái cây loại B là 20y (triệu đồng).

Vì tiền vốn là 120 triệu đồng nên 12x + 20y ≤ 120, tức là 3x + 5y ≤ 30.

Vậy x, y phải thỏa mãn hệ bất phương trình bậc nhất hai ẩn $\left\{\begin{array}{l}x+y\le 8\\ 3x+5y\le 30\\ x\ge 0\\ y\ge 0\end{array}\right.$.

Lợi nhuận thương nhân thu được là F = 1,1x + 1,5y (triệu đồng).

Từ đó, ta nhận được bài toán quy hoạch tuyến tính:

F = 1,1x + 1,5y → max

với ràng buộc $\left\{\begin{array}{l}x+y\le 8\\ 3x+5y\le 30\\ x\ge 0\\ y\ge 0.\end{array}\right.$

Giải bài toán trên như sau:

Viết lại ràng buộc của bài toán thành $\left\{\begin{array}{l}x+y-8\le 0\\ 3x+5y-30\le 0\\ x\ge 0\\ y\ge 0.\end{array}\right.$

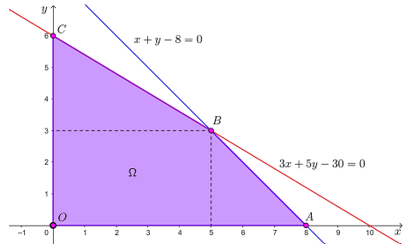
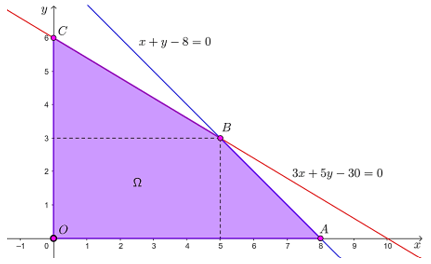
Tập phương án Ω của bài toán là miền tứ giác OABC như hình dưới đây với các đỉnh O(0; 0), A(8; 0), B(5; 3) và C(0; 6).

Giá trị của F tại các đỉnh:

F(0; 0) = 0;

F(8; 0) = 1,1 ∙ 8 + 1,5 ∙ 0 = 8,8;

F(5; 3) = 1,1 ∙ 5 + 1,5 ∙ 3 = 10;

F(0; 6) = 1,1 ∙ 0 + 1,5 ∙ 6 = 9.

Do đó, $\underset{\Omega }{\max }F=10$, đạt được khi x = 5, y = 3.

Vậy thương nhân nên mua 5 tấn trái cây loại A và 3 tấn trái cây loại B thì thu được lợi nhuận cao nhất là 10 triệu đồng khi bán hết hàng đã thu mua.

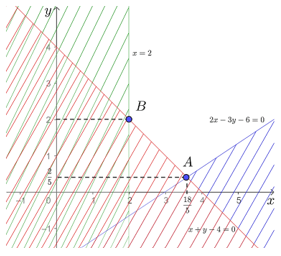
Khám phá 1 trang 6 Chuyên đề Toán 12: Xét bài toán: Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức F = x + 2y với (x; y) là nghiệm của hệ bất phương trình $\left\{\begin{array}{l}x-2y+4\ge 0\\ x+y-5\le 0\\ x\ge 0\\ y\ge 0.\end{array}\right.$ (I)

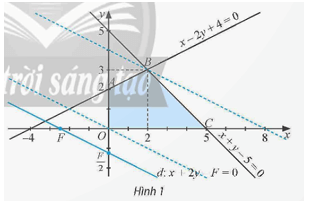
Miền nghiệm Ω của hệ (I) là miền tứ giác OABC (được tô màu) trên Hình 1. Với giá trị F cho trước, xét đường thẳng d: x + 2y – F = 0 hay $y=-\frac{x}{2}+\frac{F}{2}$.

Trả lời các câu hỏi sau để giải bài toán trên.

a) Với giá trị nào của F thì đường thẳng d đi qua điểm O, điểm B?

b) Khi giá trị của F tăng (hoặc giảm) thì tung độ giao điểm của d với trục Oy thay đổi như thế nào? Khi đó, phương của đường thẳng d có thay đổi không?

c) Với điều kiện nào của F thì đường thẳng d và miền nghiệm Ω có điểm chung?

d) Từ đó, chỉ ra giá trị lớn nhất và giá trị nhỏ nhất của biểu thức F = x + 2y trên miền nghiệm Ω. Biểu thức F đạt được các giá trị đó tại điểm nào?

Lời giải:

a)

● Đường thẳng d đi qua điểm O nên x = 0, y = 0, thay vào phương trình đường thẳng d ta được: 0 + 2 ∙ 0 – F = 0, suy ra F = 0.

● Đường thẳng d đi qua điểm B(2; 3) nên x = 2, y = 3, thay vào phương trình đường thẳng d ta được: 2 + 2 ∙ 3 – F = 0, suy ra F = 8.

b) Hoành độ giao điểm của d với trục Oy là x = 0, khi đó tung độ y = $\frac{F}{2}$.

Khi giá trị của F tăng (hoặc giảm) thì tung độ giao điểm của d với trục Oy cũng tăng (hoặc giảm).

Phương của đường thẳng d không thay đổi do không phụ thuộc vào F.

c) Đường thẳng d và miền nghiệm Ω có điểm chung khi 0 ≤ $\frac{F}{2}$ ≤ 4, tức là 0 ≤ F ≤ 8.

Vậy F ∈ [0; 8] thì đường thẳng d và miền nghiệm Ω có điểm chung.

d) Giá trị lớn nhất và giá trị nhỏ nhất của biểu thức F = x + 2y trên miền nghiệm Ω là $\underset{\Omega }{\max }F=8$, đạt được tại điểm B(2; 3).

Khám phá 2 trang 8 Chuyên đề Toán 12: Xét bài toán quy hoạch tuyến tính: F = 2x + y → max, min

với ràng buộc $\left\{\begin{array}{l}x+y-4\ge 0\\ 3x-y\ge 0\\ x\ge 0\\ y\ge 1.\end{array}\right.$(II)

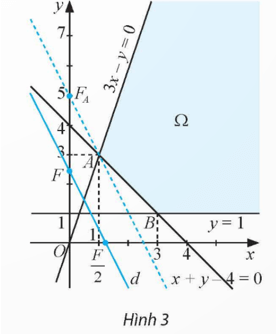
Tập phương án Ω của bài toán là phần được tô màu trên Hình 3. Hai điểm A(1; 3) và B(3; 1) gọi là các đỉnh của Ω.

Với giá trị F cho trước, xét đường thẳng d: 2x + y = F hay d: y = – 2x + F.

Trả lời các câu hỏi sau để giải bài toán trên.

a) Tìm giá trị của F để đường thẳng d đi qua điểm A(1; 3). Gọi giá trị tìm được là F_A.

b) Khi giá trị của F tăng (hoặc giảm) thì tung độ giao điểm của d với trục Oy thay đổi như thế nào? Khi đó, phương của đường thẳng d có thay đổi không?

c) Nếu F < F_A thì d và Ω có điểm chung không? Từ đó, chỉ ra giá trị nhỏ nhất của hàm mục tiêu F = 2x + y trên Ω.

d) Với giá trị nào của F thì d và Ω có điểm chung? Hàm mục tiêu F = 2x + y đạt giá trị lớn nhất trên Ω hay không?

Lời giải:

a) Đường thẳng d đi qua điểm A(1; 3) nên x = 1, y = 3, thay vào phương trình đường thẳng d, ta được F = 2 ∙ 1 + 3 = 5. Vậy F_A = 5.

b) Hoành độ giao điểm của d với trục Oy là x = 0, khi đó tung độ y = F.

Khi giá trị của F tăng (hoặc giảm) thì tung độ giao điểm của d với trục Oy cũng tăng (hoặc giảm).

Phương của đường thẳng d không thay đổi do không phụ thuộc vào F.

c) Nếu F < F_A thì d và Ω không có điểm chung.

Giá trị nhỏ nhất của hàm mục tiêu F = 2x + y trên Ω là $\underset{\Omega }{\min }F$= F_A = 5.

d) d và Ω có điểm chung khi F ≥ F_A hay F ≥ 5.

Hàm mục tiêu F = 2x + y không đạt giá trị lớn nhất trên Ω.

Thực hành 1 trang 10 Chuyên đề Toán 12: Giải bài toán quy hoạch tuyến tính: F = 4x + 3y → max, min

với ràng buộc $\left\{\begin{array}{l}x+2y-8\le 0\\ 2x-y-6\le 0\\ x\ge 0\\ y\ge 1.\end{array}\right.$

Lời giải:

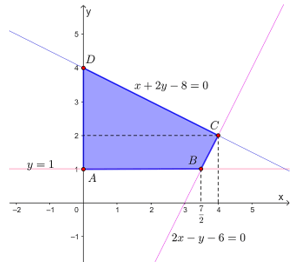
Tập phương án Ω là miền tứ giác ABCD như hình dưới đây.

Tọa độ giao điểm A của đường thẳng y = 1 và trục Oy là A(0; 1).

Tọa độ giao điểm B của hai đường thẳng y = 1 và 2x – y – 6 = 0 là nghiệm của hệ phương trình $\left\{\begin{array}{l}y=1\\ 2x-y-6=0\end{array}\right.\iff \left\{\begin{array}{l}x=\frac{7}{2}\\ y=1\end{array}\right.\Rightarrow B\left(\frac{7}{2};1\right)$.

Tương tự, ta tìm được C(4; 2) và D(0; 4).

Giá trị của biểu thức F tại các đỉnh của Ω:

F(0; 1) = 4 ∙ 0 + 3 ∙ 1 = 3;

$F\left(\frac{7}{2};1\right)=4\cdot \frac{7}{2}+3\cdot 1=17$;

F(4; 2) = 4 ∙ 4 + 3 ∙ 2 = 22;

F(0; 4) = 4 ∙ 0 + 3 ∙ 4 = 12.

Từ đó, $\underset{\Omega }{\max }F=F\left(4;2\right)=22;\underset{\Omega }{\min }F=F\left(0;1\right)=3$.

Thực hành 2 trang 10 Chuyên đề Toán 12: Giải bài toán quy hoạch tuyến tính: F = 25x + 10y → min

với ràng buộc $\left\{\begin{array}{l}2x-3y\le 6\\ x+y\ge 4\\ x\ge 2.\end{array}\right.$

Lời giải:

Viết lại ràng buộc của bài toán thành

$\left\{\begin{array}{l}2x-3y-6\le 0\\ x+y-4\ge 0\\ x\ge 2.\end{array}\right.$

Tập phương án Ω của bài toán là miền không gạch chéo trên hình dưới đây (không là miền đa giác).

Tọa độ của điểm A là nghiệm của hệ

$\left\{\begin{array}{l}2x-3y-6=0\\ x+y-4=0\end{array}\right.\iff \left\{\begin{array}{l}x=\frac{18}{5}\\ y=\frac{2}{5}\end{array}\right.\Rightarrow A\left(\frac{18}{5};\frac{2}{5}\right)$.

Tương tự, tìm được điểm B(2; 2).

Miền Ω có hai đỉnh là $A\left(\frac{18}{5};\frac{2}{5}\right)$ và B(2; 2).

Do Ω nằm trong góc phần tư thứ nhất và các hệ số của biểu thức F = 25x + 10y đều dương nên F đạt giá trị nhỏ nhất tại một đỉnh của Ω.

Ta có $F\left(\frac{18}{5};\frac{2}{5}\right)=25\cdot \frac{18}{5}+10\cdot \frac{2}{5}=94$; F(2; 2) = 25 ∙ 2 + 10 ∙ 2 = 70.

Vậy F đạt giá trị nhỏ nhất tại đỉnh B(2; 2) và $\underset{\Omega }{\min }F=F\left(2;2\right)=70$.

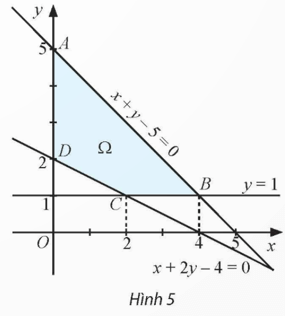
Vận dụng trang 10 Chuyên đề Toán 12: Cho bài toán quy hoạch tuyến tính F = 3x + 3y → max, min có tập phương án Ω là miền tứ giác ABCD (được tô màu như Hình 5) với các đỉnh là A(0; 5), B(4; 1), C(2; 1) và D(0; 2).

a) Giải bài toán quy hoạch tuyến tính đã cho.

b) Hàm mục tiêu F đạt giá trị lớn nhất trên Ω tại bao nhiêu điểm? Giải thích.

Lời giải:

a) Tập phương án Ω của bài toán là miền tứ giác miền tứ giác ABCD (được tô màu như Hình 5) với các đỉnh là A(0; 5), B(4; 1), C(2; 1) và D(0; 2).

Giá trị của biểu thức F tại các đỉnh của Ω:

F(0; 5) = 3 ∙ 0 + 3 ∙ 5 = 15;

F(4; 1) = 3 ∙ 4 + 3 ∙ 1 = 15;

F(2; 1) = 3 ∙ 2 + 3 ∙ 1 = 9;

F(0; 2) = 3 ∙ 0 + 3 ∙ 2 = 6.

Từ đó, $\underset{\Omega }{\max }F=F\left(0;5\right)=F\left(4;1\right)=15;\underset{\Omega }{\min }F=F\left(0;2\right)=6$.

b) Nhận thấy rằng đường thẳng AB có phương trình x + y – 5 = 0, tức là x + y = 5, nên với mọi điểm M(x; y) thuộc đường thẳng AB ta đều có

F(x; y) = 3x + 3y = 3(x + y) = 3 ∙ 5 = 15.

Vậy hàm mục tiêu F đạt giá trị lớn nhất bằng 15 tại mọi điểm M(x; y) thuộc đoạn thẳng AB. Như vậy, hàm mục tiêu F đạt giá trị lớn nhất trên Ω tại vô số điểm, đó là các điểm thuộc đoạn thẳng AB.

2. Ứng dụng vào các bài toán thực tế

Khám phá 3 trang 11 Chuyên đề Toán 12: Xét tình huống thương nhân thu mua trái cây ở Hoạt động khởi động (trang 6).

a) Nếu gọi x, y (tính theo tấn) lần lượt là khối lượng trái cây loại A và B được thương nhân thu mua thì x và y phải thoả mãn hệ bất phương trình bậc nhất hai ẩn nào?

b) Từ đó, phát biểu bài toán quy hoạch tuyến tính tìm khối lượng thu mua mỗi loại trái cây để thu được lợi nhuận cao nhất. Giải bài toán đó.

Lời giải:

a) Vì x, y (tính theo tấn) lần lượt là khối lượng trái cây loại A và B được thương nhân thu mua nên x ≥ 0 và y ≥ 0.

Thương nhân mua tối đa 8 tấn trái cây nên x + y ≤ 8.

Số tiền mua x tấn trái cây loại A là 12x (triệu đồng).

Số tiền mua y tấn trái cây loại B là 20y (triệu đồng).

Vì tiền vốn là 120 triệu đồng nên 12x + 20y ≤ 120, tức là 3x + 5y ≤ 30.

Vậy x, y phải thỏa mãn hệ bất phương trình bậc nhất hai ẩn $\left\{\begin{array}{l}x+y\le 8\\ 3x+5y\le 30\\ x\ge 0\\ y\ge 0\end{array}\right.$.

b) Lợi nhuận thương nhân thu được là F = 1,1x + 1,5y (triệu đồng).

Từ đó, ta nhận được bài toán quy hoạch tuyến tính:

F = 1,1x + 1,5y → max

với ràng buộc

$\left\{\begin{array}{l}x+y\le 8\\ 3x+5y\le 30\\ x\ge 0\\ y\ge 0.\end{array}\right.$

Giải bài toán trên như sau:

Viết lại ràng buộc của bài toán thành $\left\{\begin{array}{l}x+y-8\le 0\\ 3x+5y-30\le 0\\ x\ge 0\\ y\ge 0.\end{array}\right.$

Tập phương án Ω của bài toán là miền tứ giác OABC như hình dưới đây với các đỉnh O(0; 0), A(8; 0), B(5; 3) và C(0; 6).

Giá trị của F tại các đỉnh:

F(0; 0) = 0;

F(8; 0) = 1,1 ∙ 8 + 1,5 ∙ 0 = 8,8;

F(5; 3) = 1,1 ∙ 5 + 1,5 ∙ 3 = 10;

F(0; 6) = 1,1 ∙ 0 + 1,5 ∙ 6 = 9.

Do đó, $\underset{\Omega }{\max }F=10$, đạt được khi x = 5, y = 3.

Vậy thương nhân nên mua 5 tấn trái cây loại A và 3 tấn trái cây loại B thì thu được lợi nhuận cao nhất là 10 triệu đồng khi bán hết hàng đã thu mua.

Thực hành 3 trang 13 Chuyên đề Toán 12: Một dây chuyền của nhà máy sản xuất đá xây dựng dự định sản xuất hai loại sản phẩm A và B. Thời gian để dây chuyền sản xuất 100 tấn sản phẩm loại A và 100 tấn sản phẩm loại B lần lượt là 2 giờ và 3 giờ. Do nhu cầu thị trường, xí nghiệp sản xuất sản lượng sản phẩm loại A không ít hơn 3 lần sản lượng sản phẩm loại B. Sản phẩm loại A cho lợi nhuận là 5 triệu đồng/100 tấn; sản phẩm loại B cho lợi nhuận 9 triệu đồng/100 tấn. Trong thời gian không quá 6 giờ làm việc của dây chuyền, cần sản xuất bao nhiêu tấn sản phẩm loại A, bao nhiêu tấn sản phẩm loại B để thu được lợi nhuận cao nhất?

Lời giải:

Gọi x, y (x ≥ 0, y ≥ 0, tính theo tấn) lần lượt là khối lượng sản phẩm loại A và sản phẩm loại B cần sản xuất. Khi đó lợi nhuận thu được là P = 0,05x + 0,09y (triệu đồng).

Vì xí nghiệp sản xuất sản lượng sản phẩm loại A không ít hơn 3 lần sản lượng sản phẩm loại B nên x ≥ 3y.

Do thời gian để làm việc của dây chuyền không quá 6 giờ nên 0,02x + 0,03y ≤ 6.

Từ đó, ta nhận được bài toán quy hoạch tuyến tính:

P = 0,05x + 0,09y → max

với ràng buộc

$\left\{\begin{array}{l}x\ge 3y\\ \mathrm{0,02}x+\mathrm{0,03}y\le 6\\ x\ge 0\\ y\ge 0.\end{array}\right.$

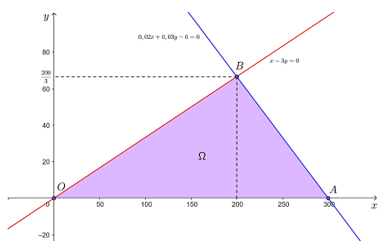
Tập phương án Ω của bài toán là miền tam giác OAB trên hình dưới đây với các đỉnh O(0; 0), A(300; 0) và $B\left(200;\frac{200}{3}\right)$.

Giá trị của P tại các đỉnh:

P(0; 0) = 0;

P(300; 0) = 0,05 ∙ 300 + 0,09 ∙ 0 = 15;

$P\left(200;\frac{200}{3}\right)=\mathrm{0,05}\cdot 200+\mathrm{0,09}\cdot \frac{200}{3}=16$.

Do đó, $\underset{\Omega }{\max }P=16$, đạt được khi x = 200, $y=\frac{200}{3}.$

Vậy trong thời gian không quá 6 giờ làm việc của dây chuyền, cần sản xuất 200 tấn sản phẩm loại A và $\frac{200}{3}$ tấn sản phẩm loại B để thu được lợi nhuận cao nhất.

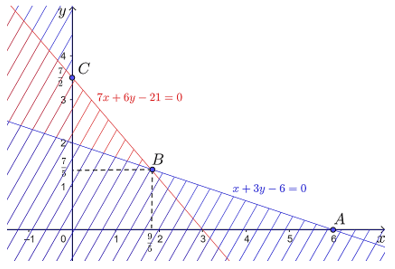
Thực hành 4 trang 13 Chuyên đề Toán 12: Trong 100 g thịt bò loại I có chứa 21 g protein và 3,5 g lipid; 100 g thịt bò loại II có chứa 18 g protein và 10,5 g lipid. Biết rằng thịt bò loại I có giá 220 nghìn đồng/kg thì thịt bò loại II có giá 210 nghìn đồng/kg. Để có lượng thực phẩm từ hai loại thịt bò trên cung cấp ít nhất 630 g protein và 210 g lipid, cần mua khối lượng bao nhiêu cho mỗi loại thịt bò loại I và II sao cho chi phí thấp nhất?

Lời giải:

Gọi x, y (x ≥ 0, y ≥ 0, tính theo kg) lần lượt là khối lượng thịt bò loại I và loại II cần mua. Từ yêu cầu để có lượng thực phẩm từ hai loại thịt bò cung cấp ít nhất 630 g protein g và 210 g lipid, ta có các bất phương trình

$\left\{\begin{array}{l}\frac{21}{\mathrm{0,1}}x+\frac{18}{\mathrm{0,1}}y\ge 630\\ \frac{\mathrm{3,5}}{\mathrm{0,1}}x+\frac{\mathrm{10,5}}{\mathrm{0,1}}y\ge 210\end{array}\right.$ hay $\left\{\begin{array}{l}7x+6y\ge 21\\ x+3y\ge 6.\end{array}\right.$

Chi phí mua x kg thịt bò loại I và y kg thịt bò loại II là F = 220x + 210y (nghìn đồng).

Từ đó, ta nhận được bài toán quy hoạch tuyến tính:

F = 220x + 210y → min

với ràng buộc

$\left\{\begin{array}{l}7x+6y\ge 21\\ x+3y\ge 6\\ x\ge 0\\ y\ge 0.\end{array}\right.$

Tập phương án Ω của bài toán là miền không gạch chéo trên hình dưới đây, có các đỉnh A(6; 0), $B\left(\frac{9}{5};\frac{7}{5}\right)$ và $C\left(0;\frac{7}{2}\right)$.

Miền Ω nằm trong góc phần từ thứ nhất, các hệ số của hàm mục tiêu F dương nên F đạt giá trị nhỏ nhất tại đỉnh của Ω.

Giá trị của F tại các đỉnh:

F(6; 0) = 220 ∙ 6 + 210 ∙ 0 = 1 320;

$F\left(\frac{9}{5};\frac{7}{5}\right)=220\cdot \frac{9}{5}+210\cdot \frac{7}{5}=690$;

$F\left(0;\frac{7}{2}\right)=220\cdot 0+210\cdot \frac{7}{2}=735$.

Suy ra $\underset{\Omega }{\min }F=690$, đạt được khi $x=\frac{9}{5}=\mathrm{1,8};y=\frac{7}{5}=\mathrm{1,4}$

Vậy cần mua 1,8 kg thịt bò loại I và 1,4 kg thịt bò loại II thì chi phí thấp nhất mà vẫn cung cấp đủ lượng protein và lipid cần thiết.

Bài 1 trang 13 Chuyên đề Toán 12: Giải bài toán quy hoạch tuyến tính: F = 8x + 5y → max, min với ràng buộc $\left\{\begin{array}{l}2x+y\le 8\\ x\ge 0\\ x\le 3\\ y\ge 1\\ y\le 5.\end{array}\right.$

Lời giải:

Viết lại ràng buộc của bài toán thành $\left\{\begin{array}{l}2x+y-8\le 0\\ x\ge 0\\ x\le 3\\ y\ge 1\\ y\le 5.\end{array}\right.$

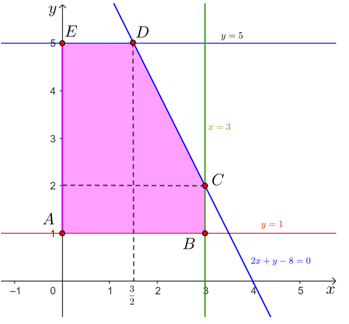
Tập phương án Ω của bài toán là miền ngũ giác ABCDE được tô màu như hình dưới đây.

Tọa độ giao điểm D của hai đường thẳng 2x + y – 8 = 0 và y = 5 là nghiệm của hệ phương trình $\left\{\begin{array}{l}2x+y-8=0\\ y=5\end{array}\right.\iff \left\{\begin{array}{l}x=\frac{3}{2}\\ y=5\end{array}\right.\Rightarrow D\left(\frac{3}{2};5\right)$.

Tương tự, ta tìm được: A(0; 1), B(3; 1), C(3; 2) và E(0; 5).

Giá trị của biểu thức F tại các đỉnh của Ω:

F(0; 1) = 8 ∙ 0 + 5 ∙ 1 = 5;

F(3; 1) = 8 ∙ 3 + 5 ∙ 1 = 29;

F(3; 2) = 8 ∙ 3 + 5 ∙ 2 = 34;

$F\left(\frac{3}{2};5\right)=8\cdot \frac{3}{2}+5\cdot 5=37$;

F(0; 5) = 8 ∙ 0 + 5 ∙ 5 = 25.

Từ đó, $\underset{\Omega }{\max }F=F\left(\frac{3}{2};5\right)=37;\underset{\Omega }{\min }F=F\left(0;1\right)=5$.

Bài 2 trang 14 Chuyên đề Toán 12: Giải bài toán quy hoạch tuyến tính: F = 10x + 20y → min với ràng buộc $\left\{\begin{array}{l}20x+5y\ge 40\\ 15x+60y\ge 120\\ x-y\le 3\\ x\ge 0\\ y\ge 0.\end{array}\right.$

Lời giải:

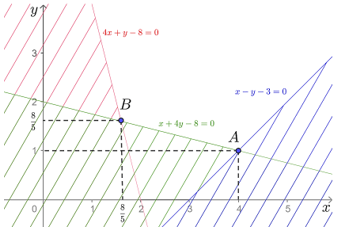
Viết lại ràng buộc của bài toán thành $\left\{\begin{array}{l}4x+y-8\ge 0\\ x+4y-8\ge 0\\ x-y-3\le 0\\ x\ge 0\\ y\ge 0.\end{array}\right.$

Tập phương án Ω của bài toán là miền không gạch chéo trên hình dưới đây (không là miền đa giác).

Tọa độ điểm A là nghiệm của hệ

$\left\{\begin{array}{l}x-y-3=0\\ x+4y-8=0\end{array}\right.\iff \left\{\begin{array}{l}x=4\\ y=1\end{array}\right.\Rightarrow A\left(4;1\right)$.

Tương tự, tìm được $B\left(\frac{8}{5};\frac{8}{5}\right)$.

Miền Ω có hai đỉnh là A(4; 1) và $B\left(\frac{8}{5};\frac{8}{5}\right)$

Do Ω nằm trong góc phần tư thứ nhất và các hệ số của biểu thức F = 10x + 20y đều dương nên F đạt giá trị nhỏ nhất tại một đỉnh của Ω.

Ta có F(4; 1) = 10 ∙ 4 + 20 ∙ 1 = 60; $F\left(\frac{8}{5};\frac{8}{5}\right)=10\cdot \frac{8}{5}+40\cdot \frac{8}{5}=80$.

Vậy F đạt giá trị nhỏ nhất tại đỉnh A(4; 1) và $\underset{\Omega }{\min }F=F\left(4;1\right)=60$.

Bài 3 trang 14 Chuyên đề Toán 12: Một cơ sở đóng thuyền thủ công cần 10 giờ lao động để đóng một thuyền loại A và 15 giờ lao động để đóng một thuyền loại B. Mỗi tuần cơ sở bổ trí được tối đa 120 giờ lao động cho việc đóng hai loại thuyền này. Qua thực tế, người ta thấy mỗi tuần cơ sở bán được tối đa 6 thuyền loại A và tối thiểu 2 thuyền loại B. Mỗi thuyền loại A, loại B cho lợi nhuận lần lượt là 0,5 triệu đồng và 0,7 triệu đồng. Mỗi tuần cơ sở nên đóng bao nhiêu thuyền mỗi loại để có thể thu được lợi nhuận cao nhất?

Lời giải:

Gọi x, y (x ≥ 0, y ≥ 0) lần lượt là số chiếc thuyền loại A và B được đóng trong một tuần.

Khi đó, lợi nhuận thu được mỗi tuần là P = 0,5x + 0,7y (triệu đồng).

Vì mỗi tuần cơ sở bán được tối đa 6 thuyền loại A và tối thiểu 2 thuyền loại B nên ta có x ≤ 6 và y ≥ 2.

Do mỗi tuần cơ sở bổ trí được tối đa 120 giờ lao động cho việc đóng hai loại thuyền nên ta có 10x + 15y ≤ 120 hay 2x + 3y ≤ 24.

Từ đó, ta nhận được bài toán quy hoạch tuyến tính:

P = 0,5x + 0,7y → max

Với ràng buộc

$\left\{\begin{array}{l}2x+3y\le 24\\ x\le 6\\ x\ge 0\\ y\ge 2.\end{array}\right.$

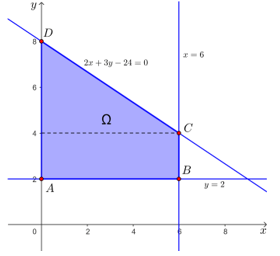
Tập phương án Ω của bài toán là miền tứ giác ABCD được tô màu như hình dưới đây với các đỉnh A(0; 2), B(6; 2), C(6; 4) và D(0; 8).

Giá trị của P tại các đỉnh:

P(0; 2) = 0,5 ∙ 0 + 0,7 ∙ 2 = 1,4;

P(6; 2) = 0,5 ∙ 6 + 0,7 ∙ 2 = 4,4;

P(6; 4) = 0,5 ∙ 6 + 0,7 ∙ 4 = 5,8;

P(0; 8) = 0,5 ∙ 0 + 0,7 ∙ 8 = 5,6.

Do đó, $\underset{\Omega }{\max }P=\mathrm{5,8}$, đạt được khi x = 6, y = 4.

Vậy mỗi tuần cơ sở đó nên đóng 6 chiếc thuyền loại A và 4 chiếc thuyền loại B thì thu được lợi nhuận cao nhất là 5,8 triệu đồng.

Bài 4 trang 14 Chuyên đề Toán 12: Để làm một chiếc bánh bao loại X cần 100 g bột mì và 60 g thịt nạc vai. Để làm một chiếc bánh bao loại Y cần 150 g bột mì và 30 g thịt nạc vai. Có thể làm được nhiều nhất bao nhiêu chiếc bánh bao từ 3 kg bột mì và 1,2 kg thịt nạc vai có sẵn? Biết rằng không thiếu các nguyên liệu khác để làm bánh.

Lời giải:

Gọi x, y (x ≥ 0, y ≥ 0) lần lượt là số chiếc bánh bao loại X và loại Y làm được.

Khi đó, số chiếc bánh bao làm được là F = x + y (chiếc).

Số bột mì cần dùng để làm x chiếc bánh bao loại X và y chiếc bánh bao loại Y không quá 3 kg nên t có bất phương trình 0,1x + 0,15y ≤ 3 hay 2x + 3y ≤ 60.

Số thịt nạc vai cần dùng để làm x chiếc bánh bao loại X và y chiếc bánh bao loại Y không quá 1,2 kg nên ta có bất phương trình 0,06x + 0,03y ≤ 1,2 hay 2x + y ≤ 40.

Từ đó, ta nhận được bài toán quy hoạch tuyến tính:

F = x + y → max

với ràng buộc

$\left\{\begin{array}{l}2x+3y\le 60\\ 2x+y\le 40\\ x\ge 0\\ y\ge 0.\end{array}\right.$

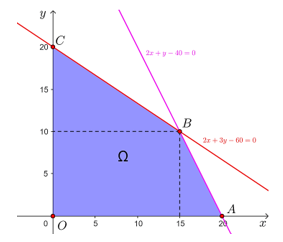
Tập phương án Ω của bài toán là miền tứ giác OABC được tô màu như hình dưới đây với các đỉnh O(0; 0), A(20; 0), B(15; 10) và C(0; 20).

Giá trị của F tại các đỉnh:

F(0; 0) = 0;

F(20; 0) = 20 + 0 = 20;

F(15; 10) = 15 + 10 = 25;

F(0; 20) = 0 + 20 = 20.

Do đó, $\underset{\Omega }{\max }F=25$, đạt được khi x = 15, y = 10.

Vậy có thể làm được nhiều nhất 25 chiếc bánh bao từ 3 kg bột mì và 1,2 kg thịt nạc vai có sẵn.

Bài 5 trang 14 Chuyên đề Toán 12: Hàm lượng các vi chất (chất vi lượng) calcium, phosphorus và iron chứa trong 100 g hai loại thực phẩm X và Y được cho ở bảng sau:

Từ hai loại thực phẩm X và Y, người ta muốn tạo ra một lượng thực phẩm hỗn hợp chứa ít nhất 2 000 mg calcium, 3 000 mg phosphorus, 48 mg iron. Cần chọn bao nhiêu gam thực phẩm mỗi loại X và Y sao cho lượng thực phẩm hỗn hợp có khối lượng nhỏ nhất?

Lời giải:

Gọi x, y (x ≥ 0, y ≥ 0, tính theo gam) lần lượt là số gam thực phẩm loại X và loại Y cần chọn để tạo ra thực phẩm hỗn hợp.

Từ yêu cầu thực phẩm hỗn hợp cần chứa ít nhất 2 000 mg calcium, 3 000 mg phosphorus, 48 mg iron, ta có các bất phương trình

$\left\{\begin{array}{l}2x+5y\ge 2000\\ 6x+3y\ge 3000\\ \mathrm{0,08}x+\mathrm{0,06}y\ge 48\end{array}\right.$ hay $\left\{\begin{array}{l}2x+5y\ge 2000\\ 2x+y\ge 1000\\ 4x+3y\ge 2400.\end{array}\right.$

Lượng thực phẩm hỗn hợp có khối lượng là F = x + y (g).

Từ đó, ta nhận được bài toán quy hoạch tuyến tính:

F = x + y → min

với ràng buộc

$\left\{\begin{array}{l}2x+5y\ge 2000\\ 2x+y\ge 1000\\ 4x+3y\ge 2400\\ x\ge 0\\ y\ge 0.\end{array}\right.$

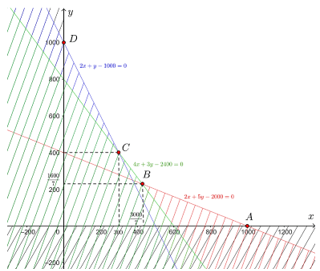
Tập phương án Ω của bài toán là miền không bị gạch chéo trên hình dưới đây, có các đỉnh là A(1 000; 0), $B\left(\frac{3000}{7};\frac{1600}{7}\right)$, C(300; 400) và D(0; 1 000).

Miền Ω nằm trong góc phần tư thứ nhất, các hệ số của hàm mục tiêu F dương nên F đạt giá trị nhỏ nhất tại đỉnh của Ω.

Giá trị của F tại các đỉnh:

F(1 000; 0) = 1 000 + 0 = 1 000;

$F\left(\frac{3000}{7};\frac{1600}{7}\right)=\frac{3000}{7}+\frac{1600}{7}=\frac{4600}{7}$;

F(300; 400) = 300 + 400 = 700;

F(0; 1 000) = 0 + 1 000 = 1 000.

Suy ra $\underset{\Omega }{\min }F=\frac{4600}{7}$, đạt được khi $x=\frac{3000}{7};y=\frac{1600}{7}$.

Vậy cần dùng $\frac{3000}{7}$g thực phẩm loại X và $\frac{1600}{7}$g thực phẩm loại Y thì lượng thực phẩm hỗn hợp có khối lượng nhỏ nhất.