Cho tam giác ABC cân tại A. Gọi G là trọng tâm, I là điểm nằm trong tam giác
Với giải Bài 40 trang 73 sgk Toán 7 Tập 2 được biên soạn lời giải chi tiết sẽ giúp học sinh biết cách làm bài tập môn Toán 7. Mời các bạn đón xem:
Giải Toán 7 Luyện tập trang 73
Video giải Bài 40 trang 73 Toán lớp 7 Tập 2
Bài 40 trang 73 Toán lớp 7 Tập 2: Cho tam giác ABC cân tại A. Gọi G là trọng tâm, I là điểm nằm trong tam giác và cách đều ba cạnh của tam giác đó. Chứng minh ba điểm A, G, I thẳng hàng.
Lời giải:
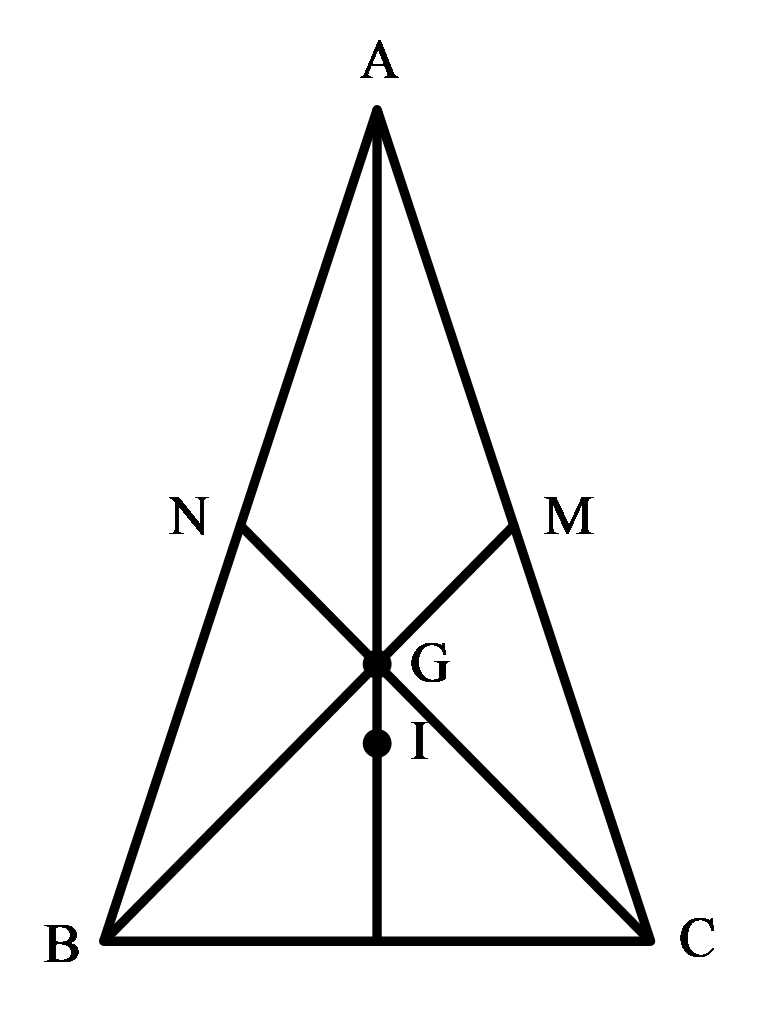
Gọi M, N lần lượt là trung điểm của CA và BA.
ΔABC cân tại A có BM, CN là đường trung tuyến ứng với cạnh AC, AB.
⇒ BM = CN (chứng minh ở bài 26).
Do G là trọng tâm tam giác ABC nên
suy ra GB = GC.
Xét ΔAGB và ΔAGC ta có:
AG là cạnh chung
AB = AC (do ΔABC cân tại A)
GB = GC (chứng minh trên)
Do đó ΔAGB = ΔAGC (c.c.c).
Suy ra .
Suy ra G thuộc tia phân giác của góc BAC.
Theo đề bài I cách đều ba cạnh của tam giác nên I là giao điểm của ba đường phân giác của tam giác ABC.
Vì G, I cùng thuộc tia phân giác của góc BAC nên A, G, I thẳng hàng.
Xem thêm lời giải bài tập Toán lớp 7 hay, chi tiết khác:
Bài 39 trang 73 Toán 7 Tập 2: Cho hình 39. a) Chứng minh ΔABD = ΔACD...
Xem thêm các chương trình khác:
