Nội dung bài viết

    Xem thêm

    Cho ba đường tròn cùng đi qua một điểm P. Gọi các giao

    Với giải câu hỏi 42 trang 107 sbt Toán lớp 9 Tập 2 được biên soạn lời giải chi tiết sẽ giúp học sinh biết cách làm bài tập môn Toán 9. Mời các bạn đón xem:

    1 647 29/03/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Giải SBT Toán 9 Bài 7: Tứ giác nội tiếp

    Bài 42 trang 107 SBT Toán 9 Tập 2: Cho ba đường tròn cùng đi qua một điểm P. Gọi các giao điểm khác P của hai trong ba đường tròn đó là A, B, C. Từ một điểm D (khác điểm P) trên đường tròn (PBC) kẻ các tia DB, DC cắt các đường tròn (PAB), (PAC) lần lượt tại M, N. Chứng minh ba điểm M, A, N thẳng hàng.

    Lời giải:

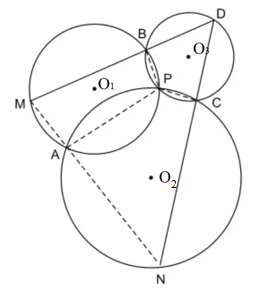
    Gọi ba đường tròn tâm O1, O2, O3

    (O1) cắt (O2) tại A; (O1) cắt (O3) tại B

    (O2) cắt (O3) tại C

    Do đó, D là điểm nằm trên đường tròn (O3)

    BD cắt (O1) tại M, DC cắt (O2) tại N

    Nối PA, PB, PC, MA, NA

    Ta có, tứ giác APBM nội tiếp đường tròn (O1)

    Nên  MAP^+MBP^=180o(tính chất tứ giác nội tiếp)

    Mà  MBP^+PBD^=180o (hai góc kề bù)

     ⇒MAP^=PBD^ (1)

    Ta có, tứ giác APCN nội tiếp đường tròn (O2)

    Nên NAP^+NCP^=180o (tính chất tứ giác nội tiếp)

    Mà NCP^+PCD^=180o (hai góc kề bù)

     ⇒NAP^=PCD^(2)

    Ta có, tứ giác BPCD nội tiếp đường tròn  (O3)

    Nên  PBD^+PCD^=180o(tính chất tứ giác nội tiếp) (3)  

    Từ (1), (2) và (3) ta suy ra: MAP^+NAP^=180o

    Vậy ba điểm M, A, N thẳng hàng.

    Xem thêm lời giải sách bài tập Toán lớp 9 hay, chi tiết khác:

    Câu hỏi 39 trang 106 SBT Toán 9 Tập 2: Trên đường tâm O có một cung AB...

    Câu hỏi 40 trang 106 SBT Toán 9 Tập 2: Cho tam giác ABC....

    Câu hỏi 41 trang 106 SBT Toán 9 Tập 2: Cho tam giác cân ABC có đáy BC...

    Câu hỏi 43 trang 107 SBT Toán 9 Tập 2: Cho đoạn thẳng AC và BD cắt nhau tại...

    Bài tập bổ sung

    Câu hỏi 7.1 trang 107 SBT Toán 9 Tập 2: Cho tam giác ABC có ba góc nhọn...

    Câu hỏi 7.2 trang 107 SBT Toán 9 Tập 2: Cho đường tròn tâm O bán kính R...

    Tham khảo các loạt bài Toán 9 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 647 29/03/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: