Câu hỏi:
22/07/2024 114
Xét tính liên tục của các hàm số sau:
a) f(x) = x3 ‒ x2 + 2; b) f(x)=x+1x2−4x;
c) f(x)=2x−1x2−x+1; d) f(x)=√x2−2x .
Xét tính liên tục của các hàm số sau:
a) f(x) = x3 ‒ x2 + 2; b) f(x)=x+1x2−4x;
c) f(x)=2x−1x2−x+1; d) f(x)=√x2−2x .
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
a) f(x) là hàm đa thức có tập xác định là ℝ nên nó liên tục trên ℝ.
b) Ta có: x2 ‒ 4x ≠ 0 ⇔ x ≠ 0 và x ≠ 4.
f(x) là hàm số phân thức có tập xác định D = ℝ ∖ {0; 4} nên nó liên tục trên các khoảng (‒∞; 0), (0; 4) và (4; +∞).
c) Ta có: x2−x+1=(x−12)2+34>0,∀x∈ℝ
f(x) là hàm số phân thức có tập xác định ℝ nên nó liên tục trên ℝ.
d) Ta có: x2 ‒ 2x ≥ 0 ⇔ x ≤ 0 và x ≥ 2
f(x) là hàm số phân thức có tập xác định D = (‒∞; 0] ∪ [2; +∞) nên nó liên tục trên các khoảng (‒∞; 0] và [2; +∞).
a) f(x) là hàm đa thức có tập xác định là ℝ nên nó liên tục trên ℝ.
b) Ta có: x2 ‒ 4x ≠ 0 ⇔ x ≠ 0 và x ≠ 4.
f(x) là hàm số phân thức có tập xác định D = ℝ ∖ {0; 4} nên nó liên tục trên các khoảng (‒∞; 0), (0; 4) và (4; +∞).
c) Ta có: x2−x+1=(x−12)2+34>0,∀x∈ℝ
f(x) là hàm số phân thức có tập xác định ℝ nên nó liên tục trên ℝ.
d) Ta có: x2 ‒ 2x ≥ 0 ⇔ x ≤ 0 và x ≥ 2
f(x) là hàm số phân thức có tập xác định D = (‒∞; 0] ∪ [2; +∞) nên nó liên tục trên các khoảng (‒∞; 0] và [2; +∞).
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): x2 + (y ‒ 1)2 = 1. Với mỗi số thực m, gọi Q(m) là số giao điểm của đường thẳng d: y = m với đường tròn (C). Viết công thức xác định hàm số y = Q(m). Hàm số này không liên tục tại các điểm nào?
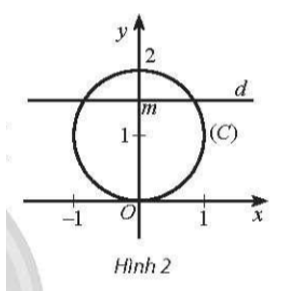
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): x2 + (y ‒ 1)2 = 1. Với mỗi số thực m, gọi Q(m) là số giao điểm của đường thẳng d: y = m với đường tròn (C). Viết công thức xác định hàm số y = Q(m). Hàm số này không liên tục tại các điểm nào?

Câu 3:
Cho hàm số y=f(x)={x2+ax+b khi |x|<2x(2−x) khi |x|≥2.
Tìm giá trị của các tham số a và b sao cho hàm số y = f(x) liên tục trên ℝ.
Cho hàm số y=f(x)={x2+ax+b khi |x|<2x(2−x) khi |x|≥2.
Tìm giá trị của các tham số a và b sao cho hàm số y = f(x) liên tục trên ℝ.
Câu 4:
Xét tính liên tục của mỗi hàm số sau tại điểm x = 2.
a) f(x)={6−2x khi x≥22x2−6 khi x<2. b)f(x)={x2−4x−2 khi x≠20 khi x=2.
Xét tính liên tục của mỗi hàm số sau tại điểm x = 2.
a) f(x)={6−2x khi x≥22x2−6 khi x<2. b)f(x)={x2−4x−2 khi x≠20 khi x=2.
Câu 5:
Chứng minh rằng phương trình:
a) x3 + 2x ‒ 1 = 0 có nghiệm thuộc khoảng (‒1; 1).
b) √x2+x+x2=1 có nghiệm thuộc khoảng (0; 1).
Chứng minh rằng phương trình:
a) x3 + 2x ‒ 1 = 0 có nghiệm thuộc khoảng (‒1; 1).
b) √x2+x+x2=1 có nghiệm thuộc khoảng (0; 1).
Câu 6:
Cho hai hàm số f(x) = x ‒ 1 và g(x) = x2 ‒ 3x + 2. Xét tính liên tục của các hàm số:
a) y = f(x).g(x); b) y=f(x)g(x); c) y=1√f(x)+g(x).
Cho hai hàm số f(x) = x ‒ 1 và g(x) = x2 ‒ 3x + 2. Xét tính liên tục của các hàm số:
a) y = f(x).g(x); b) y=f(x)g(x); c) y=1√f(x)+g(x).
Câu 7:
Xét tính liên tục của hàm số:
a) f(x)=|x+1| tại điểm x = ‒1; b) g(x)={|x−1|x−1khi x≠11khi x=1 tại điểm x = 1.
Xét tính liên tục của hàm số:
a) f(x)=|x+1| tại điểm x = ‒1; b) g(x)={|x−1|x−1khi x≠11khi x=1 tại điểm x = 1.
Câu 8:
Cho hai hàm số f(x)={2−x khi x<1x2+x khi x≥1 và g(x)={2x−x2 khi x<1−x2+a khi x≥1.
Tìm giá trị của tham số a sao cho hàm số h(x) = f(x) + g(x) liên tục tại x = 1.
Cho hai hàm số f(x)={2−x khi x<1x2+x khi x≥1 và g(x)={2x−x2 khi x<1−x2+a khi x≥1.
Tìm giá trị của tham số a sao cho hàm số h(x) = f(x) + g(x) liên tục tại x = 1.
Câu 9:
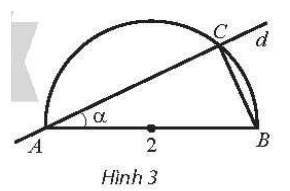
Cho nửa đường tròn đường kính AB = 2. Đường thẳng d thay đổi luôn đi qua A, cắt nửa đường tròn tại C và tạo với đường thẳng AB góc α(0<α<π2) .
Kí hiệu diện tích tam giác ABC là S(α) (phụ thuộc vào α). Xét tính liên tục của hàm số S(α) trên khoảng (0;π2) và tính các giới hạn limα→0+S(α),limα→π2S(α).
Cho nửa đường tròn đường kính AB = 2. Đường thẳng d thay đổi luôn đi qua A, cắt nửa đường tròn tại C và tạo với đường thẳng AB góc α(0<α<π2) .
Kí hiệu diện tích tam giác ABC là S(α) (phụ thuộc vào α). Xét tính liên tục của hàm số S(α) trên khoảng (0;π2) và tính các giới hạn limα→0+S(α),limα→π2S(α).

Câu 10:
Dùng định nghĩa, xét tính liên tục của hàm số:
a) f(x) = x3 ‒ 3x + 2 tại điểm x = ‒2;
b) f(x)=√3x+2 tại điểm x = 0.
Dùng định nghĩa, xét tính liên tục của hàm số:
a) f(x) = x3 ‒ 3x + 2 tại điểm x = ‒2;
b) f(x)=√3x+2 tại điểm x = 0.
Câu 11:
Xét tính liên tục của các hàm số sau:
a) f(x)=tanx√1−x2; b) f(x)=1sinx .
Xét tính liên tục của các hàm số sau:
a) f(x)=tanx√1−x2; b) f(x)=1sinx .


