Giải SBT Toán 11 CTST Bài 3. Hàm số liên tục
-
99 lượt thi
-
12 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 5:
22/07/2024Xét tính liên tục của các hàm số sau:
a) f(x) = x3 ‒ x2 + 2; b)
c) d) .
Xem đáp án
a) f(x) là hàm đa thức có tập xác định là ℝ nên nó liên tục trên ℝ.
b) Ta có: x2 ‒ 4x ≠ 0 ⇔ x ≠ 0 và x ≠ 4.
f(x) là hàm số phân thức có tập xác định D = ℝ ∖ {0; 4} nên nó liên tục trên các khoảng (‒∞; 0), (0; 4) và (4; +∞).
c) Ta có:
f(x) là hàm số phân thức có tập xác định ℝ nên nó liên tục trên ℝ.
d) Ta có: x2 ‒ 2x ≥ 0 ⇔ x ≤ 0 và x ≥ 2
f(x) là hàm số phân thức có tập xác định D = (‒∞; 0] ∪ [2; +∞) nên nó liên tục trên các khoảng (‒∞; 0] và [2; +∞).
Câu 11:
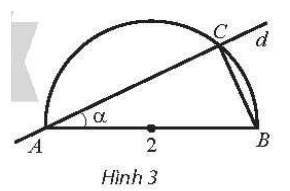
22/07/2024Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): x2 + (y ‒ 1)2 = 1. Với mỗi số thực m, gọi Q(m) là số giao điểm của đường thẳng d: y = m với đường tròn (C). Viết công thức xác định hàm số y = Q(m). Hàm số này không liên tục tại các điểm nào?
Xem đáp án
Ta có:
Ta có nên
Do đó hàm số y = Q(m) không liên tục tại m = 0.
Tương tự ta cũng có hàm số y = Q(m) không liên tục tại m = 2.
Vậy hàm số không liên tục tại các điểm m = 0 và m = 2.
