Câu hỏi:
17/07/2024 220Xếp ngẫu nhiên 21 học sinh, trong đó có đúng một bạn tên Thêm và đúng một bạn tên Quý vào ba bàn tròn có số chỗ ngồi lần lượt là 6, 7, 8. Xác suất để hai bạn Thêm và Quý ngồi cạnh nhau bằng
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn A
Đánh số ba bàn tròn có số chỗ ngồi lần lượt là 6, 7, 8 là bàn 1, bàn 2, bàn 3.
+) Xét phép thử: “Xếp ngẫu nhiên 21 học sinh vào ba bàn tròn 1, 2, 3 nói trên”.
Chọn 6 học sinh trong số 21 học sinh và xếp vào bàn 1 có ![]() cách.
cách.
Chọn 7 học sinh trong số 15 học sinh còn lại và xếp vào bàn 2 có ![]() cách.
cách.
Xếp 8 học sinh còn lại vào bàn 3 có 7! cách.
Suy ra số phần tử của không gian mẫu là ![]()
+) Gọi A là biến cố: “ Hai bạn Thêm và Quý luôn ngồi cạnh nhau ”.
Trường hợp 1: Hai bạn Thêm và Quý ngồi bàn 1.
Chọn 4 học sinh từ 19 học sinh còn lại có cách.
Xếp 4 học sinh vừa chọn và hai bạn Thêm, Quý vào bàn 1 có 4!.2! cách.
Chọn 7 học sinh từ 15 học sinh còn lại và xếp vào bàn 2 có ![]() cách.
cách.
Xếp 8 học sinh còn lại vào bàn 3 có 7! cách.
Số cách xếp thỏa mãn trường hợp 1 là: ![]()
Trường hợp 2: Hai bạn Thêm và Quý ngồi bàn 2.
Tương tự như trên, ta có số cách xếp thỏa mãn trường hợp 2 là ![]()
Trường hợp 3: Hai bạn Thêm và Quý ngồi bàn 3.
Tương tự như trên, ta có số cách xếp thỏa mãn trường hợp 3 là: ![]()
![]()
![]()
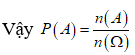
= =
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Tổ 1 của lớp 10A có 10 học sinh gồm 6 nam và 4 nữ. Cần chọn ra 2 bạn trong tổ 1 để phân công trực nhật. Xác suất để chọn được 1 bạn nam và 1 bạn nữ là
Câu 2:
Xếp ngẫu nhiên 4 quyển sách Toán khác nhau và 4 quyển sách Hóa giống nhau vào một giá sách nằm ngang có 10 ô trống, mỗi quyển sách được xếp vào một ô. Xác suất để 4 quyển sách Toán xếp cạnh nhau và 4 quyển sách Hóa xếp cạnh nhau bằng
Câu 3:
Xếp ngẫu nhiên 10 học sinh gồm 2 học sinh khối 10, 5 học sinh khối 11 và 3 học sinh khối 12 thành một hàng ngang. Xác suất để không có học sinh khối 11 nào xếp giữa hai học sinh khối 10 bằng
Câu 4:
Có một dãy ghế gồm 6 ghế. Xếp ngẫu nhiên 6 học sinh gồm 2 học sinh lớp A, 2 học sinh lớp B, 2 học sinh lớp C ngồi vào dãy ghế sao cho mỗi ghế có đúng một học sinh ngồi. Xác suất để không có học sinh lớp C nào ngồi cạnh nhau bằng
Câu 5:
Một hộp đựng 7 viên bi đỏ đánh số từ 1 đến 7 và 6 viên bi xanh đánh số từ 1 đến 6. Hỏi có bao nhiêu cách chọn hai viên bi từ hộp đó sao cho chúng khác màu và khác số?
Câu 6:
Trên kệ sách có 10 cuốn sách Toán và 5 cuốn sách Văn. Người ta lấy ngẫu nhiên lần lượt 3 cuốn sách mà không để lại. Tính xác suất để được hai cuốn sách đầu là Toán, cuốn thứ ba là Văn.
Câu 7:
Cho hình tứ diện đều ABCD. Trên mỗi cạnh của tứ diện, ta đánh dấu 3 điểm chia đều cạnh tương ứng thành các phần bằng nhau. Gọi S là tập hợp các tam giác có ba đỉnh lấy từ 18 điểm đã đánh dấu. Lấy ra từ S một tam giác, xác suất để mặt phẳng chứa tam giác đó song song với đúng một cạnh của tứ diện đã cho bằng
Câu 8:
Gọi S là tập hợp các số tự nhiên, mỗi số không có quá 3 chữ số và tổng các chữ số bằng 9. Lấy ngẫu nhiên một số từ ![]() . Tính xác suất để số lấy ra có chữ số hàng trăm là 4.
. Tính xác suất để số lấy ra có chữ số hàng trăm là 4.
Câu 9:
Cho tập hợp A có 20 phần tử. Có bao nhiêu tập con của A khác rỗng và số phần tử là số chẵn?
Câu 10:
Với các chữ “LẬP”, “HỌC”, “MAI”, “NGÀY”, “NGHIỆP”, “TẬP”, “VÌ”, mỗi chữ được viết lên một tấm bìa, sau đó người ta trải ra ngẫu nhiên. Xác suất để được dòng chữ “HỌC TẬP VÌ NGÀY MAI LẬP NGHIỆP” bằng:
Câu 11:
Một hộp có 10 quả cầu xanh, 5 quả cầu đỏ. Lấy ngẫu nhiên 5 quả từ hộp đó. Xác suất để được 5 quả có đủ hai màu là
Câu 12:
Cho tập hợp S = {1;2;3;4;5;6;7;8;9}. Chọn ngẫu nhiên ba số từ tập S. Tính xác suất của biến cố trong ba số được chọn ra không chứa hai số nguyên liên tiếp nào.
Câu 13:
Một tổ học sinh có 7 học sinh nam và 3 học sinh nữ. Chọn ngẫu nhiên 2 người. Tính xác suất sao cho 2 người được chọn đều là nữ.
Câu 15:
Gieo một con súc sắc cân đối và đồng chất. Giả sử súc sắc xuất hiện mặt b chấm. Xác suất để phương trình + 2bx + 4 = 0 có nghiệm là


