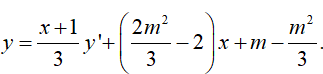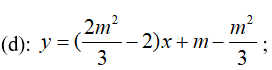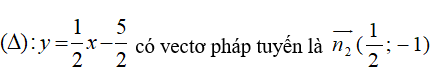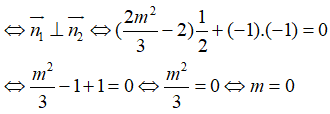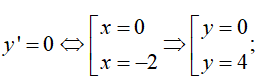Câu hỏi:
16/07/2024 270Với giá trị nào của m, đồ thị hàm số có hai điểm cực trị đối xứng qua đường thẳng:
A. m = 0
B. m = 1
C. m = -1
D. Không tồn tại
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn D
Hàm số có hai điểm cực trị => y’=0 có hai nghiệm phân biệt <=> <=>
Chia y cho y’ ta được:
Giả sử là hai nghiệm phân biệt của y’=0.
Phương trình đường thẳng đi qua hai điểm cực trị có dạng
(d) có vectơ pháp tuyến là
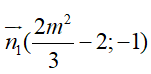
Vì hai điểm cực trị đối xứng với nhau qua (Δ) nên (d) ⊥ (Δ)
Thử lại khi m=0 ta có:
y''(0) = 6 > 0; y''(-2) = -6 < 0
Tọa độ hai điểm cực trị của đồ thị hàm số là O(0;0), A(-2;4)
Trung điểm của OA là I(-1;2).
Ta thấy I(-1,2) không thuộc đường thẳng (Δ) . Vậy không tồn tại m.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Tìm tất cả các giá trị của tham số m để hàm số đạt cực đại tại x = 1.
Câu 2:
Với giá trị nào của m, đường thẳng đi qua hai điểm cực trị của đồ thị hàm số tạo với đường thẳng Δ: 3x + y - 8 = 0 một góc ?
Câu 3:
Cho hàm số y = f(x) có đồ thị như hình vẽ. Điểm cực đại của đồ thị hàm số là
Câu 4:
Cho hàm số f có đạo hàm là với mọi x ∈ R. Số điểm cực trị của hàm số f là:
Câu 6:
Cho hàm số Phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số trên là:
Câu 8:
Đồ thị hàm số y = |x| có dạng hình vẽ.
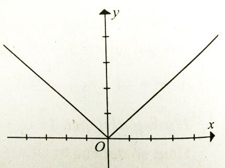
Có bao nhiêu mệnh đề đúng trong các phát biểu sau?
1. Hàm số không có đạo hàm tại x = 0.
2. Hàm số không liên tục tại x = 0.
3. Hàm số không có cực trị tại x = 0.
4. Hàm số đạt cực trị tại x = 0.
Câu 13:
Cho hàm số (1) và các mệnh đề
(1) Điểm cực trị của hàm số (1) là x = 0 hoặc x = 4/3
(2) Điểm cực trị của hàm số (1) là x = 0 và x = 4/3
(3) Điểm cực trị của đồ thị hàm số (1) là x = 0 và x = 4/3
(4) Cực trị của hàm số (1) là x = 0 và x = 4/3
Trong các mệnh đề trên, số mệnh đề sai là:
Câu 14:
Tìm a, b, c sao cho hàm số có giá trị bằng 0 khi x = 1 và đạt cực trị khi bằng 0 khi x = -1 .