Câu hỏi:
11/07/2024 91
Từ đồ thị hàm số y = sin x, tìm:
Các giá trị của x để sin x = 12;
Từ đồ thị hàm số y = sin x, tìm:
Các giá trị của x để sin x = 12;
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Xét đồ thị hàm số y = sin x và đường thẳng y = 12.
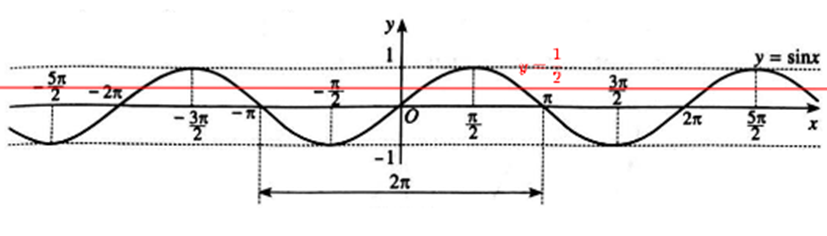
Giá trị của x để sin x = 12 là hoành độ giao điểm của đồ thị hàm số y = sin x và đường thẳng y = 12.
Dựa vào đồ thị, ta có sin x = 12 khi x=π6+k2π và x=5π6+k2π với k ∈ ℤ.
Xét đồ thị hàm số y = sin x và đường thẳng y = 12.

Giá trị của x để sin x = 12 là hoành độ giao điểm của đồ thị hàm số y = sin x và đường thẳng y = 12.
Dựa vào đồ thị, ta có sin x = 12 khi x=π6+k2π và x=5π6+k2π với k ∈ ℤ.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số:
y=√1+cos2x+3;
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số:
y=√1+cos2x+3;
Câu 3:
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số:
y = 4 – 2sin x cos x;
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số:
y = 4 – 2sin x cos x;
Câu 4:
Hàm số nào sau đây là hàm số lẻ?
A. y = – 2cos x.
B. y = – 2sin x.
C. y = tan x – cos x.
D. y = – 2 sin x + 2.
Hàm số nào sau đây là hàm số lẻ?
A. y = – 2cos x.
B. y = – 2sin x.
C. y = tan x – cos x.
D. y = – 2 sin x + 2.
Câu 5:
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số:
y=14−sinx.
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số:
y=14−sinx.
Câu 6:
Từ đồ thị hàm số y = cos x, cho biết:
Có bao nhiêu giá trị của x trên khoảng (−9π2;−3π2) để cos x = 0.
Từ đồ thị hàm số y = cos x, cho biết:
Có bao nhiêu giá trị của x trên khoảng (−9π2;−3π2) để cos x = 0.
Câu 8:
Tập xác định của hàm số y=tanx+11+cot2x là:
A. R∖{kπ2|k∈Z}.
B. R∖{−π4+kπ|k∈Z}.
C. R∖{π4+kπ|k∈Z}.
D. R∖{−π4+k2π|k∈Z}.
Tập xác định của hàm số y=tanx+11+cot2x là:
A. R∖{kπ2|k∈Z}.
B. R∖{−π4+kπ|k∈Z}.
C. R∖{π4+kπ|k∈Z}.
D. R∖{−π4+k2π|k∈Z}.
Câu 11:
Từ đồ thị hàm số y = cos x, cho biết:
Có bao nhiêu giá trị của x trên đoạn [ – 5π; 0] để cos x = 1;
Từ đồ thị hàm số y = cos x, cho biết:
Có bao nhiêu giá trị của x trên đoạn [ – 5π; 0] để cos x = 1;
Câu 12:
Hàm số nào trong các hàm số sau đồng biến trên khoảng (π2;3π2)?
A. y = sin x.
B. y = cos x.
C. y = tan x.
D. y = cot x.
Hàm số nào trong các hàm số sau đồng biến trên khoảng (π2;3π2)?
A. y = sin x.
B. y = cos x.
C. y = tan x.
D. y = cot x.Câu 13:
Một vòng quay trò chơi có bán kính 57 m, trục quay cách mặt đất 57,5 m, quay đều mỗi vòng hết 15 phút. Khi vòng quay quay đều, khoảng cách h (m) từ một cabin gắn tại điểm A của vòng quay đến mặt đất được tính bởi công thức:
h(t)=57sin(2π15t−π2)+57,5
với t là thời gian quay của vòng quay tính bằng phút (t ≥ 0) (Hình 12).
Khi quay một vòng lần thứ nhất tính từ thời điểm t = 0 (phút), tại thời điểm nào của t thì cabin ở vị trí cao nhất? Ở vị trí đạt được chiều cao là 86 m?
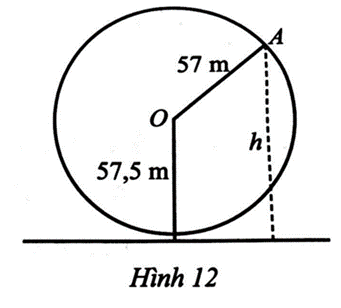
Một vòng quay trò chơi có bán kính 57 m, trục quay cách mặt đất 57,5 m, quay đều mỗi vòng hết 15 phút. Khi vòng quay quay đều, khoảng cách h (m) từ một cabin gắn tại điểm A của vòng quay đến mặt đất được tính bởi công thức:
h(t)=57sin(2π15t−π2)+57,5
với t là thời gian quay của vòng quay tính bằng phút (t ≥ 0) (Hình 12).
Khi quay một vòng lần thứ nhất tính từ thời điểm t = 0 (phút), tại thời điểm nào của t thì cabin ở vị trí cao nhất? Ở vị trí đạt được chiều cao là 86 m?

Câu 15:
Xét sự biến thiên của mỗi hàm số sau trên các khoảng tương ứng:
y = cosx trên khoảng (19π; 20π), (– 30π; – 29π).
Xét sự biến thiên của mỗi hàm số sau trên các khoảng tương ứng:
y = cosx trên khoảng (19π; 20π), (– 30π; – 29π).


