Câu hỏi:
17/07/2024 189Từ các chữ số thuộc tập X = {0;1;2;3;4;5;6;7} có thể lập được bao nhiêu số tự nhiên gồm 6 chữ số khác nhau sao cho mỗi số tự nhiên đó đều chia hết cho 18.
A. 720.
B. 860.
C. 984.
D. 1228.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn C
Giả sử số lập được có dạng ![]()
![]()
Ta có 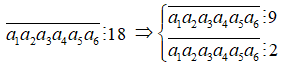
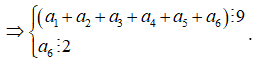
Vì ![]() nên ta có các trường hợp sau
nên ta có các trường hợp sau
Trường hợp 1: được chọn từ ![]()
+ Có 3 cách chọn chọn
+ Có 5! cách chọn chọn bộ 5 số ![]()
Suy ra có 3.5! = 360 số.
Trường hợp 2: được chọn từ ![]()
+ = 0, có 5! cách chọn bộ 5 số ![]()
+ 0 khi đó có 3 cách chọn, có 4 cách chọn và có 4! cách chọn bộ 4 số ![]()
Suy ra có 5! + 3.4.4!= 408 số
Trường hợp 3: được chọn từ ![]()
+ = 0, có 5! cách chọn bộ 5 số ![]()
+ 0 khi đó có 1 cách chọn, có 4 cách chọn và có 4! cách chọn bộ 4 số ![]()
Suy ra có 5! + 1.4.4! = 216 số
Vậy có: 360 + 408 + 216 = 984 số.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 3:
Từ các chữ số 0, 1, 2, 3, 4, 5, 6, 7 có thể lập được bao nhiêu số tự nhiên có 5 chữ số đôi một khác nhau sao cho có đúng 3 chữ số chẵn và 2 chữ số lẻ, đồng thời hai chữ số lẻ đứng liền nhau?
Câu 4:
Cho một hình vuông có cạnh bằng 4. Chia hình vuông này thành 16 hình vuông đơn vị có cạnh bằng 1. Hỏi có bao nhiêu tam giác có các đỉnh là các đỉnh của hình vuông đơn vị?
Câu 5:
Có bao nhiêu đường thẳng cắt Hypebol y = tại hai điểm phân biệt mà cả hai điểm đó đều có tọa độ nguyên ?
Câu 7:
Từ các chữ số 0, 1, 2, 3, 4, 5, 6, 7 có thể lập được bao nhiêu số tự nhiên có 5 chữ số đôi một khác nhau sao cho có đúng 3 chữ số chẵn và 2 chữ số lẻ, đồng thời ba chữ số chẵn đứng liền nhau?
Câu 10:
Từ các chữ số 0, 1, 2, 3, 4, 5, 6, 7 có thể lập được bao nhiêu số tự nhiên có 5 chữ số đôi một khác nhau sao cho có đúng 3 chữ số chẵn và 2 chữ số lẻ, đồng thời ba chữ số chẵn đứng liền nhau và hai chữ số lẻ đứng liền nhau?
Câu 11:
Trong mặt phẳng cho 10 điểm phân biệt. Số vectơ khác , có điểm đầu và điểm cuối lấy trong các điểm đã cho là
Câu 12:
Một lớp có 33 học sinh, cần chọn ra 6 học sinh để trực trường vào buổi chiều. Hỏi có bao nhiêu cách chọn?
Câu 13:
Cho số nguyên dương n và hệ số của trong khai triển Newton của bằng 31.Khi đó n bằng
Câu 14:
Sắp xếp 20 người vào 2 bàn tròn A, B phân biệt, mỗi bàn gồm 10 chỗ ngồi. Số cách sắp xếp là


