Câu hỏi:
17/07/2024 175Từ các chữ số 0; 1; 2;3 ; 4; 5 có thể lập được bao nhiêu số chẵn gồm 4 chữ số khác nhau
A. 156
B. 144
C. 96
D. 134
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn A
Gọi số cần tìm có dạng 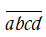
Vì 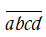
TH1. Nếu d = 0 số cần tìm là 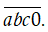
a được chọn từ tập A\{0} nên có 5 cách chọn.
b được chọn từ tập A\{0,a} nên có 4 cách chọn.
c được chọn từ tập A\{0,a,b} nên có 3 cách chọn.
Như vậy, ta có 5.4.3 = 60 số có dạng
TH2. Nếu d = {2,4} ⇒ d có 2 cách chọn.
Khi đó a: có 4 cách chọn (khác 0 và d),
b: có 4 cách chọn và c có 3 cách chọn.
Như vậy, ta có 2.4.4.3 = 96 số cần tìm như trên.
Vậy có tất cả 60 +96 = 156 số cần tìm.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Có bao nhiêu số tự nhiên gồm 7 chữ số khác nhau đôi một, trong đó chữ số 2 đứng liền giữa hai chữ số 1 và 3?
Câu 4:
Có 5 tem thư khác nhau và 6 bì thư khác nhau. Từ đó người ta muốn chọn ra 3 tem thư, 3 bì thư và dán 3 tem thư ấy lên 3 bì đã chọn. Hỏi có bao nhiêu cách làm như thế?
Câu 5:
Cho hai đường thẳng song song a và b Trên a lấy 17 điểm phân biệt, trên b lấy 20 điểm phân biệt. Tính số tam giác mà có các đỉnh được chọn từ 37 điểm này.
Câu 8:
Một hộp có 5 viên bi xanh, 6 viên bi đỏ và 7 viên bi vàng. Chọn ngẫu nhiên 5 viên bi trong hộp, tính xác suất để 5 viên bi được chọn có đủ màu và số bi đỏ bằng số bi vàng.
Câu 10:
Một hộp chứa 3 viên bi xanh, 5 viên bi đỏ và 6 viên bi vàng. Lấy ngẫu nhiên 6 viên bi từ hộp, tính xác suất để 6 viên bi được lấy ra có đủ cả ba màu.
Câu 11:
Một cuộc thi có 15 người tham dự, giả thiết rằng không có hai người nào có điểm bằng nhau. Nếu kết quả cuộc thi và việc chọn ra 4 người có điểm cao nhất thì có bao nhiêu kết quả có thể xảy ra?
Câu 15:
Ảnh của đường thẳng d: -3x + 4y + 5 = 0 qua phép đối xứng trục Ox là đường thẳng nào sau đây


