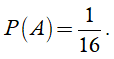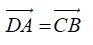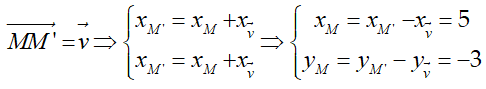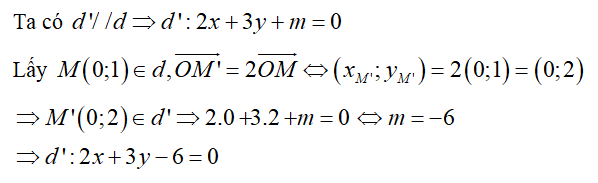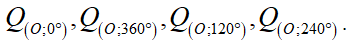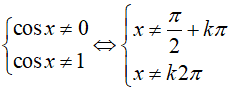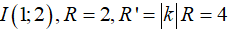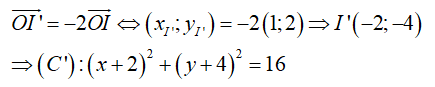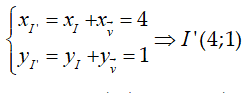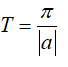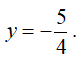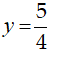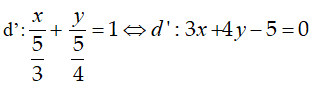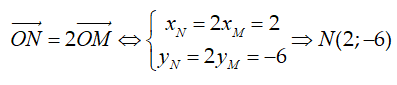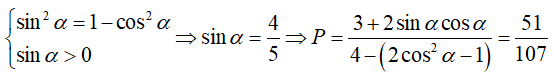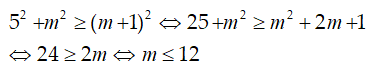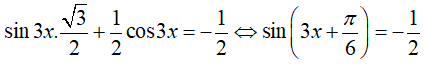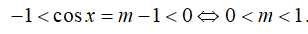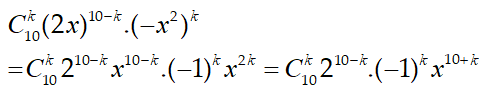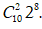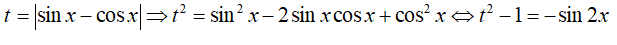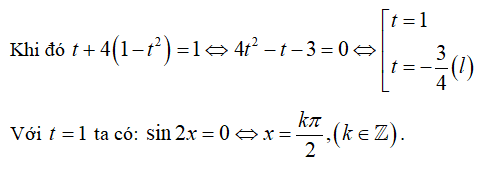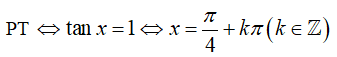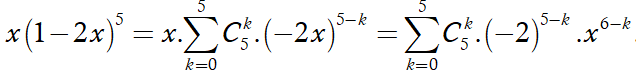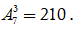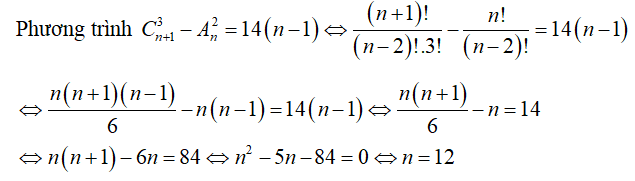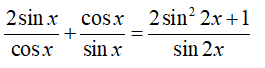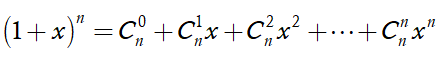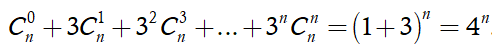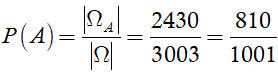Đề thi Toán 11 Học kì 1 có đáp án (Đề 4)
-
825 lượt thi
-
40 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 2:
17/07/2024Gieo một đồng tiền cân đối và đồng chất bốn lần. Xác suất để cả bốn lần xuất hiện mặt sấp là?
 Xem đáp án
Xem đáp án
Chọn C
Số phần tử của không gian mẫu là
Gọi A là biến cố Cả bốn lần gieo xuất hiện mặt sấp n(A) = 1
Vậy xác suất cần tính
Câu 3:
23/07/2024Cho hình bình hành ABCD. Phép tịnh tiến biến:
 Xem đáp án
Xem đáp án
Chọn C
Vì ABCD là hình bình hành nên:
Phép tịnh tiến 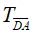
Câu 4:
17/07/2024Một cuộc thi có 15 người tham dự, giả thiết rằng không có hai người nào có điểm bằng nhau. Nếu kết quả cuộc thi và việc chọn ra 4 người có điểm cao nhất thì có bao nhiêu kết quả có thể xảy ra?
 Xem đáp án
Xem đáp án
Chọn D
Nếu kết quả cuộc thi là việc chọn ra 4 người có điểm cao nhất thì mỗi kết quả ứng với một tổ hợp chập 4 của 15 phần tử.
Như vậy, ta có 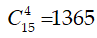
Câu 5:
17/07/2024Tính chất nào sau đây không phải là tính chất của phép dời hình?
 Xem đáp án
Xem đáp án
Chọn D
Tính chất D sai vì hai đoạn thẳng đó bằng nhau
Câu 6:
17/07/2024Giả sử bạn muốn mua một áo sơ mi cỡ 39 hoặc cỡ 40. Áo cỡ 39 có 5 màu khác nhau, áo cỡ 40 có 4 màu khác nhau. Hỏi có bao nhiêu sự lựa chọn (về màu áo và cỡ áo)?
 Xem đáp án
Xem đáp án
Chọn A
Nếu chọn cỡ áo 39 thì sẽ có 5 cách.
Nếu chọn cỡ áo 40 thì sẽ có 4 cách.
Theo qui tắc cộng, ta có 5 + 4 = 9 cách chọn mua áo.
Câu 7:
16/07/2024Cho và điểm M'(4;2). Biết M' là ảnh của M qua phép tịnh tiến . Tìm M.
 Xem đáp án
Xem đáp án
Chọn A
Ta có:
Vậy M (5; -3)
Câu 9:
17/07/2024Trong mặt phẳng Oxy cho đường thẳng d có phương trình 2x + 3y - 3 = 0. Ảnh của đường thẳng d qua phép vị tự tâm O tỉ số k = 2 biến đường thẳng d thành đường thẳng có phương trình là:
 Xem đáp án
Xem đáp án
Chọn A
Câu 10:
21/07/2024Cho hai đường thẳng song song a và b Trên a lấy 17 điểm phân biệt, trên b lấy 20 điểm phân biệt. Tính số tam giác mà có các đỉnh được chọn từ 37 điểm này.
 Xem đáp án
Xem đáp án
Chọn C
Một tam giác được tạo bởi ba điểm phân biệt nên ta xét:
TH1. Chọn 1 điểm thuộc a và 2 điểm thuộc b có 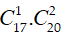
TH2. Chọn 2 điểm thuộc a và 1 điểm thuộc b có 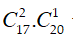
Như vậy, ta có 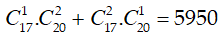
Câu 11:
17/07/2024Có bao nhiêu phép quay tâm O góc α, 0 ≤ α ≤ 2π , biến tam giác đều có tâm O thành chính nó
 Xem đáp án
Xem đáp án
Chọn A
Các phép quay thỏa mãn bài toán là
Câu 13:
17/07/2024Trong mặt phẳng Oxy cho đường tròn (C) có phương trình . Hỏi phép vị tự tâm O tỉ số k = -2 biến (C) thành đường tròn nào sau đây:
 Xem đáp án
Xem đáp án
Chọn C
Đường tròn (C ) có tâm
Phép vị tự tâm O, tỉ số k = -2; biến tâm I thành tâm I’ nên:
Câu 14:
16/07/2024Cho và đường tròn . Ảnh của (C) qua là (C')
 Xem đáp án
Xem đáp án
Chọn B
Đường tròn (C ) có tâm I(1; -2) và R = 3.
Tinh tiến theo 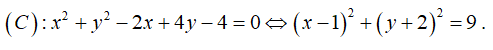
Đường tròn (C’) có tâm I’ ( 4; 1) và bán kính R’ = R = 3 có phương trình:
Câu 16:
17/07/2024Có 5 tem thư khác nhau và 6 bì thư khác nhau. Từ đó người ta muốn chọn ra 3 tem thư, 3 bì thư và dán 3 tem thư ấy lên 3 bì đã chọn. Hỏi có bao nhiêu cách làm như thế?
 Xem đáp án
Xem đáp án
Chọn B
Số cách chọn 3 tem thư trong 5 tem thư khác nhau là: 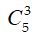
Số cách chọn 3 bì thư trong 6 bì thư khác nhau là: 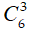
Số cách dán tem thư thứ nhất vào 3 bì thư là: 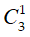
Số cách dán tem thư thứ hai vào 2 bì thư còn lại là: 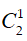
Số cách dán tem thư thứ hai vào bì thư cuối cùng là: 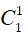
Vậy có 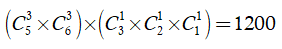
Câu 17:
17/07/2024Ảnh của đường thẳng d: -3x + 4y + 5 = 0 qua phép đối xứng trục Ox là đường thẳng nào sau đây
 Xem đáp án
Xem đáp án
Chọn A
Đường thẳng d cắt trục Ox tại điểm có hoành độ 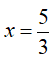
Đường thẳng d' là ảnh của đường thẳng d qua phép đối xứng trục Ox cắt trục Ox tại điểm có hoành độ 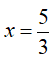
Phương trình đoạn chắn của
Câu 18:
23/07/2024Một hộp có 5 viên bi xanh, 6 viên bi đỏ và 7 viên bi vàng. Chọn ngẫu nhiên 5 viên bi trong hộp, tính xác suất để 5 viên bi được chọn có đủ màu và số bi đỏ bằng số bi vàng.
 Xem đáp án
Xem đáp án
Chọn B
Không gian mẫu là số cách chọn ngẫu nhiên 5 viên bi từ hộp chứa 18 viên bi. Suy ra số phần tử của không gian mẫu là 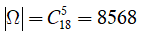
Gọi A là biến cố 5 viên bi được chọn có đủ màu và số bi đỏ bằng số bi vàng . Ta có các trường hợp thuận lợi cho biến cố A là :
● TH1: Chọn 1 bi đỏ, 1 bi vàng và 3 bi xanh nên có 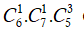
● TH2: Chọn 2 bi đỏ, 2 bi vàng và 1 bi xanh nên có 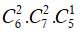
Suy ra số phần tử của biến cố A là 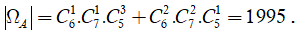
Vậy xác suất cần tính 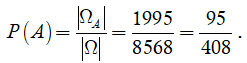
Câu 19:
16/07/2024Ảnh của điểm P(-1;3) qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép quay tâm O(0;0) góc quay và phép vị tự tâm O(0;0) tỉ số 2 là
 Xem đáp án
Xem đáp án
Chọn A
Gọi M(x;y) là ảnh của P qua phép quay tâm O, góc quay 180°.
Khi đó O là trung điểm của MP suy ra M(1;-3) .
Phép vị tự tâm O, tỉ số k = 2 biến điểm M thành điểm N nên:
Câu 21:
17/07/2024Trong một hộp chứa sáu quả cầu trắng được đánh số từ 1 đến 6 và ba quả cầu đen được đánh số 7; 8; 9 Có bao nhiêu cách chọn một trong các quả cầu ấy?
 Xem đáp án
Xem đáp án
Chọn B
Vì các quả cầu trắng hoặc đen đều được đánh số phân biệt nên mỗi lần lấy ra một quả cầu bất kì là một lần chọn.
Nếu chọn một quả trắng có 6 cách.
Nếu chọn một quả đen có 3 cách.
Theo qui tắc cộng, ta có 6 + 3= 9 cách chọn.
Câu 22:
19/07/2024Tìm m để phương trình 5cosx - msinx = m + 1 có nghiệm
 Xem đáp án
Xem đáp án
Chọn C
Để phương trình đã cho có nghiệm khi:
Câu 23:
17/07/2024Sắp xếp năm bạn học sinh An, Bình, Chi, Dũng, Lệ vào một chiếc ghế dài có 5 chỗ ngồi. Số cách sắp xếp sao cho bạn Chi luôn ngồi chính giữa là
 Xem đáp án
Xem đáp án
Chọn A
Xếp bạn Chi ngồi giữa có 1 cách.
Số cách xếp 4 bạn sinh An, Bình, Dũng, Lệ vào 4 chỗ còn lại là một hoán vị của 4 phần tử nên có có 4! = 24 cách.
Vậy có 24 cách xếp.
Câu 25:
16/07/2024Một thùng trong đó có 12 hộp đựng bút màu đỏ, 18hộp đựng bút màu xanh. Số cách khác nhau để chọn được đồng thời một hộp màu đỏ, một hộp màu xanh là?
 Xem đáp án
Xem đáp án
Chọn D
Để chọn một hộp màu đỏ và một hộp màu xanh, ta có:
Có 12 cách chọn hộp màu đỏ.
Có 18 cách chọn hộp màu xanh.
Vậy theo qui tắc nhân ta có 12. 18 = 216 cách.
Câu 26:
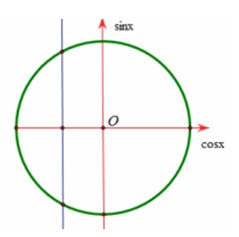
23/07/2024Phương trình 1 + cosx = m có đúng 2 nghiệm khi và chỉ khi:
 Xem đáp án
Xem đáp án
Chọn A
Phương trình đã cho có 2 nghiệm 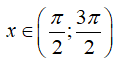
Câu 27:
16/07/2024Tìm hệ số của trong khai triển
 Xem đáp án
Xem đáp án
Chọn B
Theo khai triển nhị thức Niu-tơn, ta có
Số hạng đứng thứ k + 1 là:
Hệ số của ứng với 10 + k = 12 nên k = 2
Hệ số cần tìm
Câu 29:
20/07/2024Số 253125000 có bao nhiêu ước số tự nhiên?
 Xem đáp án
Xem đáp án
Chọn C
Ta có: 253125000 = 23. 34. 58 nên mỗi ước số tự nhiên của số đã cho đều có dạng trong đó m,n,p ∈ N sao cho 0 ≤ m ≤ 3 ; 0 ≤ n ≤ 4; 0 ≤ p ≤ 8
Có 4 cách chọn m
Có 5 cách chọn n
Có 9 cách chọn p
Vậy theo qui tắc nhân ta có 4.5.9 = 180 ước số tự nhiên.
Câu 31:
16/07/2024Tìm hệ số của trong khai triển
 Xem đáp án
Xem đáp án
Chọn C
Theo khai triển nhị thức Niu-tơn, ta có
số hạng chứa tương ứng với 6- k = 5 nên k = 1 .
Tương tự, ta có
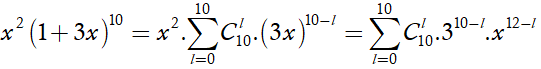
số hạng chứa tương ứng với 12 – l= 5 hay l = 7.
Vậy hệ số của cần tìm là
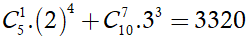
Câu 32:
16/07/2024Trong một ban chấp hành đoàn gồm 7 người, cần chọn ra 3 người vào ban thường vụ. Nếu cần chọn ban thường vụ gồm ba chức vụ Bí thư, Phó bí thư, Ủy viên thường vụ thì có bao nhiêu cách chọn?
 Xem đáp án
Xem đáp án
Chọn A
Số cách chọn ban thường vụ gồm ba chức vụ Bí thư, Phó bí thư, Ủy viên thường vụ từ 7 người là số các chỉnh hợp chập ba của bảy phần tử
Câu 34:
17/07/2024Từ các chữ số 0; 1; 2;3 ; 4; 5 có thể lập được bao nhiêu số chẵn gồm 4 chữ số khác nhau
 Xem đáp án
Xem đáp án
Chọn A
Gọi số cần tìm có dạng 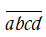
Vì 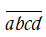
TH1. Nếu d = 0 số cần tìm là 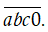
a được chọn từ tập A\{0} nên có 5 cách chọn.
b được chọn từ tập A\{0,a} nên có 4 cách chọn.
c được chọn từ tập A\{0,a,b} nên có 3 cách chọn.
Như vậy, ta có 5.4.3 = 60 số có dạng
TH2. Nếu d = {2,4} ⇒ d có 2 cách chọn.
Khi đó a: có 4 cách chọn (khác 0 và d),
b: có 4 cách chọn và c có 3 cách chọn.
Như vậy, ta có 2.4.4.3 = 96 số cần tìm như trên.
Vậy có tất cả 60 +96 = 156 số cần tìm.
Câu 35:
22/07/2024Nghiệm của phương trình là
 Xem đáp án
Xem đáp án
Chọn B
Điều kiện: sin2x ≠ 0 .
Phương trình tương đương
Câu 36:
22/07/2024Có bao nhiêu số tự nhiên gồm 7 chữ số khác nhau đôi một, trong đó chữ số 2 đứng liền giữa hai chữ số 1 và 3?
 Xem đáp án
Xem đáp án
Chọn B
Ta chia thành các trường hợp sau:
TH1: Nếu số 123 đứng đầu thì có 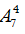
TH2: Nếu số 321 đứng đầu thì có 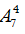
TH3: Nếu số 123; 321 không đứng đầu
Khi đó có 6 cách chọn số đứng đầu ( khác 0; 1; 2; 3 ),
khi đó còn 6 vị trí có 4 cách xếp 3 số 321 hoặc 123, còn lại 3 vị trí có 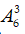
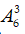
Suy ra tổng các số thoả mãn yêu cầu là 2.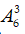
Câu 37:
16/07/2024Tính tổng
 Xem đáp án
Xem đáp án
Chọn D
Khai triển nhị thức Niu-tơn của (1 + x)n , ta có
Cho x = 3, ta được:
Câu 38:
22/07/2024Một hộp chứa 3 viên bi xanh, 5 viên bi đỏ và 6 viên bi vàng. Lấy ngẫu nhiên 6 viên bi từ hộp, tính xác suất để 6 viên bi được lấy ra có đủ cả ba màu.
 Xem đáp án
Xem đáp án
Chọn A
Không gian mẫu là số cách chọn ngẫu nhiên 6 viên bi từ hộp chứa 14 viên bi. Suy ra số phần tử của không gian mẫu là 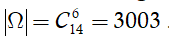
Gọi A là biến cố 6 viên bi được lấy ra có đủ cả ba màu
Để tìm số phần tử của biến cố A ta đi tìm số phần tử của biến cố 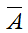
● TH1: Chọn 6 viên bi chỉ có một màu (chỉ chọn được màu vàng).
Do đó trường hợp này có 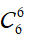
● TH2: Chọn 6 viên bi có đúng hai màu xanh và đỏ, có 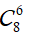
Chọn 6 viên bi có đúng hai màu đỏ và vàng, có 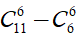
Chọn 6 viên bi có đúng hai màu xanh và vàng, có 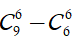
Do đó trường hợp này có 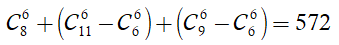
Suy ra số phần tử của biến cố 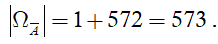
Suy ra số phần tử của biến cố 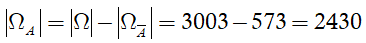
Vậy xác suất cần tính
Câu 39:
21/07/2024Trong các mệnh đề sau, mệnh đề nào đúng?
 Xem đáp án
Xem đáp án
Chọn D
A sai. Trong trường hợp 2 đường thẳng cắt nhau thì chúng chỉ có 1 điểm chung.
B và C sai. Hai đường thẳng song song khi và chỉ khi chúng đồng phằng và không có điểm chung.
Câu 40:
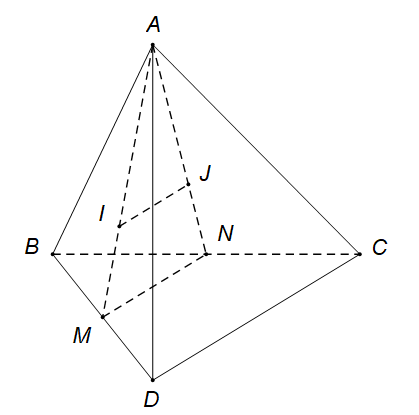
17/07/2024Cho tứ diện ABCD. Gọi I; J lần lượt là trọng tâm các tam giác ABD và ABC. Chọn khẳng định đúng trong các khẳng định sau?
 Xem đáp án
Xem đáp án
Chọn A
Gọi M;N lần lượt là trung điểm của BD; BC
là đường trung bình của tam giác BCD ⇒ MN // CD
Vì I; J lần lượt là trọng tâm các tam giác ABD và ABC ⇒
Từ (1) và (2) suy ra: IJ // CD
Bài thi liên quan
-
Đề thi Toán 11 Học kì 1 có đáp án (Đề 1)
-
24 câu hỏi
-
60 phút
-
-
Đề thi Toán 11 Học kì 1 có đáp án (Đề 2)
-
50 câu hỏi
-
60 phút
-
-
Đề thi Toán 11 Học kì 1 có đáp án (Đề 3)
-
50 câu hỏi
-
60 phút
-
Có thể bạn quan tâm
- Đề thi Toán 11 giữa kì 1 có đáp án (4346 lượt thi)
- Đề thi Học kì 1 Toán lớp 11 năm 2020 - 2021 có đáp án (840 lượt thi)
- Đề thi Toán 11 Học kì 1 có đáp án (824 lượt thi)
Các bài thi hot trong chương
- Đề thi Toán 11 Học kì 2 có đáp án (1167 lượt thi)
- Đề thi Học kì 2 Toán 11 có đáp án (839 lượt thi)