Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải:
Vì góc \(\widehat {xOz}\) và \(\widehat {yOz}\) là hai góc kề bù nên:
\(\widehat {xOz}\) + \(\widehat {yOz}\) = 180o
60o + \(\widehat {yOz}\) = 1800
\(\widehat {yOz}\) = 180o – 600
\(\widehat {yOz}\) = 120o
Lại có: On là tia phân giác của góc \(\widehat {yOz}\), do đó:
\(\widehat {yOn} = \widehat {nOz} = \frac{{\widehat {yOz}}}{2} = \frac{{120^\circ }}{2} = 60^\circ \)
Vậy \(\widehat {yOn} = 60^\circ \).
Hướng dẫn giải:
Vì góc \(\widehat {xOz}\) và \(\widehat {yOz}\) là hai góc kề bù nên:
\(\widehat {xOz}\) + \(\widehat {yOz}\) = 180o
60o + \(\widehat {yOz}\) = 1800
\(\widehat {yOz}\) = 180o – 600
\(\widehat {yOz}\) = 120o
Lại có: On là tia phân giác của góc \(\widehat {yOz}\), do đó:
\(\widehat {yOn} = \widehat {nOz} = \frac{{\widehat {yOz}}}{2} = \frac{{120^\circ }}{2} = 60^\circ \)
Vậy \(\widehat {yOn} = 60^\circ \).
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Vẽ \(\widehat {xOy} = 60^\circ \). Vẽ tia Oz là tia đối của tia Ox. Vẽ tia Om là tia phân giác của góc zOy.
Tính \[\widehat {zOm}\].
Câu 2:
Vẽ hai đường thẳng xy và mn cắt nhau tại điểm O sao cho \(\widehat {xOm} = 120^\circ \). Tính các góc \(\widehat {mOy};\widehat {yOn};\widehat {xOn}\).
Câu 3:
Vẽ \[\widehat {xAy} = 40^\circ \]. Vẽ \(\widehat {yAz}\) là góc kề bù với \[\widehat {xAy}\].
Câu 4:
Vẽ \(\widehat {xAm} = 50^\circ \). Vẽ tia phân giác An của \(\widehat {xAm}\).
Tính \(\widehat {xAn}\).
Câu 6:
Cho góc bẹt xOy. Vẽ tia Oz sao cho \(\widehat {xOz} = 60^\circ \). Vẽ tia Om là tia phân giác của góc xOz. Vẽ tia On là tia phân giác của góc zOy.
Tính số đo góc xOm.
Cho góc bẹt xOy. Vẽ tia Oz sao cho \(\widehat {xOz} = 60^\circ \). Vẽ tia Om là tia phân giác của góc xOz. Vẽ tia On là tia phân giác của góc zOy.
Tính số đo góc xOm.
Câu 7:
Vẽ tia On là tia đối của tia Om. Tia Ox có phải là tia phân giác của góc yOn không? Vì sao?
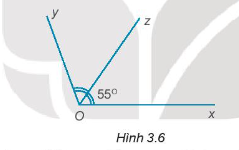
Câu 8:
Cho Hình 3.6. Biết tia Oz là tia phân giác của \(\widehat {xOy}\). Tính \(\widehat {xOy}\)