Giải SBT Toán 7 Bài 8: Góc ở vị trí đặc biệt. Tia phân giác của một góc có đáp án
Giải SBT Toán 7 Bài 8: Góc ở vị trí đặc biệt. Tia phân giác của một góc có đáp án
-
79 lượt thi
-
13 câu hỏi
-
40 phút
Danh sách câu hỏi
Câu 1:
16/07/2024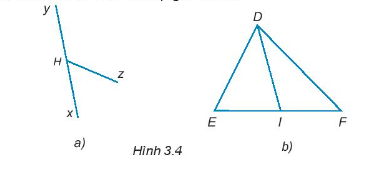
 Xem đáp án
Xem đáp án
Lời giải:
Các cặp góc kề bù có trong hình là:
Hình 3.4a: \(\widehat {xHz}\) và \(\widehat {yHz}\)
Hình 3.4b: \(\widehat {EID}\) và \(\widehat {FID}\).
Câu 2:
19/07/2024Cho Hình 3.5
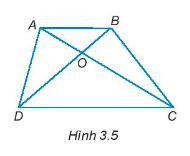
Gọi tên các cặp góc đối đỉnh.
 Xem đáp án
Xem đáp án
Lời giải:
Các cặp góc đối đỉnh là: \(\widehat {AOB}\) và \(\widehat {DOC}\); \(\widehat {AOD}\) và \(\widehat {BOC}\).
Câu 3:
23/07/2024 Xem đáp án
Xem đáp án
Câu 4:
16/07/2024 Xem đáp án
Xem đáp án
Lời giải:
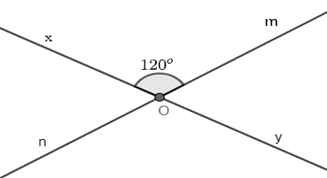
Vì góc \(\widehat {xOm}\) và góc \(\widehat {nOy}\)là hai góc đối đỉnh nên \(\widehat {xOm}\) = \(\widehat {nOy} = 120^\circ \)
Vì góc \(\widehat {xOn}\) và góc \(\widehat {xOm}\) là hai góc kề bù nên \(\widehat {xOn}\) + \(\widehat {xOm} = 180^\circ \)
\(\widehat {xOn}\) + \(120^\circ = 180^\circ \)
\(\widehat {xOn}\) = 180o – 120o
\(\widehat {xOn}\) = 60o.
Mà \(\widehat {xOn}\) và \(\widehat {yOm}\) đối đỉnh nên \(\widehat {xOn}\) = \(\widehat {yOm}\) = 60o.
Câu 5:
22/07/2024Vẽ \(\widehat {xAm} = 50^\circ \). Vẽ tia phân giác An của \(\widehat {xAm}\).
Tính \(\widehat {xAn}\).
 Xem đáp án
Xem đáp án
Lời giải:
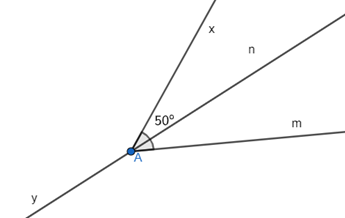
Vì An là tia phân giác của góc \(\widehat {xAm}\) nên \(\widehat {xAn} = \widehat {mAn} = \frac{{\widehat {xAM}}}{2} = \frac{{50^\circ }}{2} = 25^\circ \).
Câu 6:
21/07/2024 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Vì tia Ay là tia đối của tia An nên \(\widehat {yAn} = 180^\circ \)
Do đó, \(\widehat {nAm}\) và góc \(\widehat {mAy}\) là hai góc kề bù.
Ta có:
\(\widehat {nAm}\) + \(\widehat {mAy}\) = 180o
25o + \(\widehat {mAy}\) = 180o
\(\widehat {mAy}\) = 180o – 25o
\(\widehat {mAy}\) = 155o.
Vậy \(\widehat {mAy}\) = 155o.
Câu 7:
16/07/2024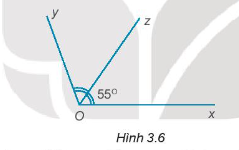
 Xem đáp án
Xem đáp án
Lời giải:
Vì Oz là tia phân giác của góc \(\widehat {xOy}\) nên \(\widehat {xOz} = \widehat {zOy} = \frac{{\widehat {xOy}}}{2} = 55^\circ \).
Do đó, \(\widehat {xOy} = 55^\circ .2 = 110^\circ \).
Vậy \(\widehat {xOy} = 110^\circ \).
Câu 8:
22/07/2024 Xem đáp án
Xem đáp án
Lời giải:
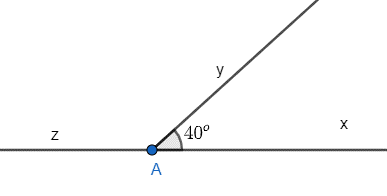
Câu 9:
16/07/2024Cho góc bẹt xOy. Vẽ tia Oz sao cho \(\widehat {xOz} = 60^\circ \). Vẽ tia Om là tia phân giác của góc xOz. Vẽ tia On là tia phân giác của góc zOy.
Tính số đo góc xOm.
 Xem đáp án
Xem đáp án
Lời giải:
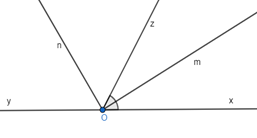
Vì Om là tia phân giác của góc \(\widehat {xOz}\) nên \(\widehat {xOm} = \widehat {mOz} = \frac{{\widehat {xOz}}}{2} = \frac{{60^\circ }}{2} = 30^\circ \)
Vậy \(\widehat {xOm} = 30^\circ \).
Câu 10:
17/07/2024Tính số đo góc yOn.
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Vì góc \(\widehat {xOz}\) và \(\widehat {yOz}\) là hai góc kề bù nên:
\(\widehat {xOz}\) + \(\widehat {yOz}\) = 180o
60o + \(\widehat {yOz}\) = 1800
\(\widehat {yOz}\) = 180o – 600
\(\widehat {yOz}\) = 120o
Lại có: On là tia phân giác của góc \(\widehat {yOz}\), do đó:
\(\widehat {yOn} = \widehat {nOz} = \frac{{\widehat {yOz}}}{2} = \frac{{120^\circ }}{2} = 60^\circ \)
Vậy \(\widehat {yOn} = 60^\circ \).
Câu 11:
16/07/2024Tính số đo góc mOn.
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Ta có: \(\widehat {mOn} = \widehat {mOz} + \widehat {zOn}\)
\(\widehat {mOn} = 30^\circ + 60^\circ = 90^\circ \)
Vậy \(\widehat {mOn} = 90^\circ \).
Câu 12:
19/07/2024Vẽ \(\widehat {xOy} = 60^\circ \). Vẽ tia Oz là tia đối của tia Ox. Vẽ tia Om là tia phân giác của góc zOy.
Tính \[\widehat {zOm}\].
 Xem đáp án
Xem đáp án
Lời giải:
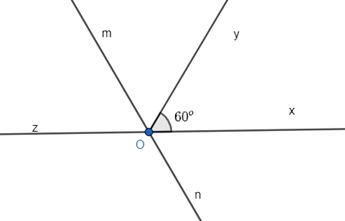
Vì Oz và Ox là hai tia đối nhau nên \(\widehat {zOx} = 180^\circ \). Do đó, \(\widehat {zOy}\) và \(\widehat {yOx}\) là hai góc kề bù.
\(\widehat {zOy}\) + \(\widehat {yOx}\) = 180o
\(\widehat {zOy}\) + 60o = 180o
\(\widehat {zOy}\) = 180o – 60o
\(\widehat {zOy}\) = 120o.
Mà Om là tia phân giác của góc \(\widehat {zOy}\) nên ta có:
\(\widehat {zOm} = \widehat {mOy} = \frac{{\widehat {zOy}}}{2} = \frac{{120^\circ }}{2} = 60^\circ \)
Vậy \[\widehat {zOm}\] = 60o.
Câu 13:
20/07/2024 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Vì On là tia đối của tia Om và Oz là tia đối của tia Ox nên \(\widehat {mOz};\widehat {nOx}\) đối đỉnh.
Suy ra,
\(\widehat {mOz} = \widehat {nOx}\) = 60o.
Ta có: Ox nằm giữa hai tia Oy và On;
\(\widehat {xOy} = \widehat {nOx}\) = 60o.
Do đó, Ox là tia phân giác của góc \(\widehat {yOn}\).
