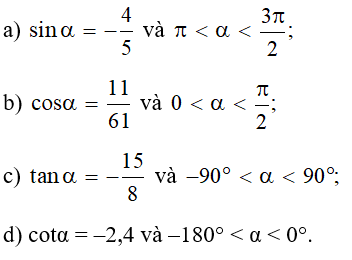Câu hỏi:
14/07/2024 122
Tính giá trị của các biểu thức sau:
a) sin 17°sin197° + sin73°cos163°;
b)
Tính giá trị của các biểu thức sau:
a) sin 17°sin197° + sin73°cos163°;
b)
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
a) Ta có:
sin197° = sin(180° + 17°) = ‒sin17°.
sin73° = sin(90° ‒ 17°) = cos17°.
cos163° = cos(180° ‒ 17°) = ‒cos17°.
Suy ra:
sin 17°sin197° + sin73°cos163°
= sin 17°.(‒sin17°) + cos17°.(‒cos17°)
= ‒(sin217° + cos217°) = ‒1.
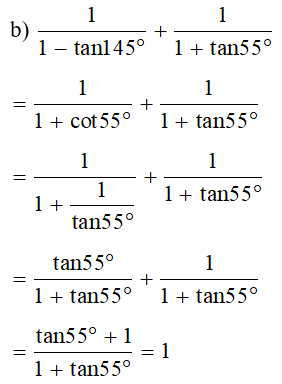
a) Ta có:
sin197° = sin(180° + 17°) = ‒sin17°.
sin73° = sin(90° ‒ 17°) = cos17°.
cos163° = cos(180° ‒ 17°) = ‒cos17°.
Suy ra:
sin 17°sin197° + sin73°cos163°
= sin 17°.(‒sin17°) + cos17°.(‒cos17°)
= ‒(sin217° + cos217°) = ‒1.
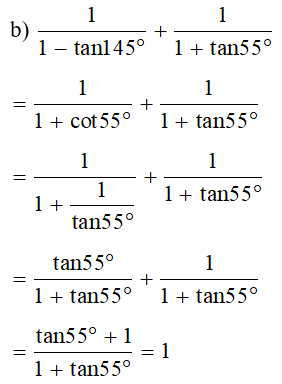
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 3:
Độ dài của ngày từ lúc Mặt Trời mọc đến lúc Mặt Trời mọc ở một thành phố X trong ngày thứ t của năm được tính xấp xỉ bởi công thức:
với t ∈ ℤ và 1 ≤ t ≤ 365.
Thành phố X vào ngày 31 tháng 1 có bao nhiêu giờ có Mặt Trời chiếu sáng? Làm tròn kết quả đến hàng phần mười.
Độ dài của ngày từ lúc Mặt Trời mọc đến lúc Mặt Trời mọc ở một thành phố X trong ngày thứ t của năm được tính xấp xỉ bởi công thức:
với t ∈ ℤ và 1 ≤ t ≤ 365.
Thành phố X vào ngày 31 tháng 1 có bao nhiêu giờ có Mặt Trời chiếu sáng? Làm tròn kết quả đến hàng phần mười.
Câu 5:
Chứng minh các đẳng thức lượng giác sau:
a) sin4x + cos4x = 1 ‒ 2sin2xcos2x.
b)
c)
d)
Chứng minh các đẳng thức lượng giác sau:
a) sin4x + cos4x = 1 ‒ 2sin2xcos2x.
b)
c)
d)
Câu 6:
Biểu diễn các giá trị lượng giác sau qua các giá trị lượng giác của góc có số đo từ 0 đến (hoặc từ 0° đến 45°).
a) sin(‒1693°);
b)
c) tan 885°;
d)
Biểu diễn các giá trị lượng giác sau qua các giá trị lượng giác của góc có số đo từ 0 đến (hoặc từ 0° đến 45°).
a) sin(‒1693°);
b)
c) tan 885°;
d)
Câu 10:
a) Cho tanα + cotα = 2. Tính giá trị của biểu thức tan3α +cot3α.
b) Cho Tính giá trị của sinαcosα.
c) Cho Tính giá tị của biểu thức sin3α + cos3α.
a) Cho tanα + cotα = 2. Tính giá trị của biểu thức tan3α +cot3α.
b) Cho Tính giá trị của sinαcosα.
c) Cho Tính giá tị của biểu thức sin3α + cos3α.