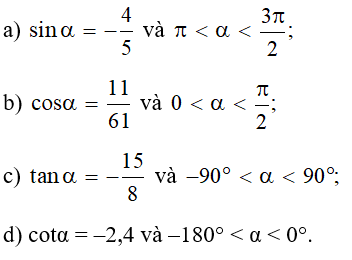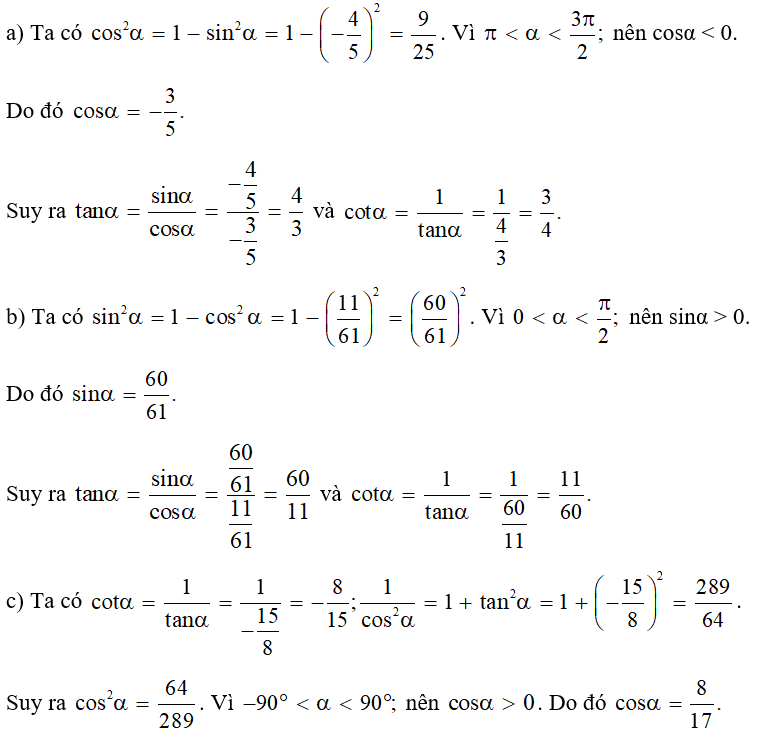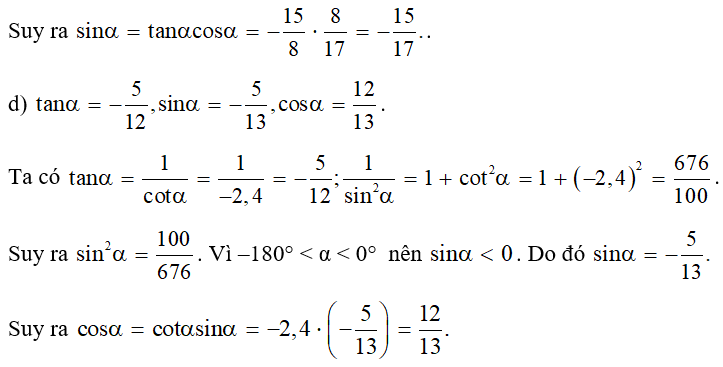Giải SBT Toán 11 CTST Bài 2. Giá trị lượng giác của một góc lượng giác
Giải SBT Toán 11 CTST Bài 2. Giá trị lượng giác của một góc lượng giác
-
66 lượt thi
-
11 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 2:
06/07/2024Biểu diễn các giá trị lượng giác sau qua các giá trị lượng giác của góc có số đo từ 0 đến (hoặc từ 0° đến 45°).
a) sin(‒1693°);
b)
c) tan 885°;
d)
 Xem đáp án
Xem đáp án
a) sin(‒1693°) = ‒sin(1693°)
= ‒sin(4.360° + 180° + 73°)
= sin73°
= cos(90° ‒ 73°) = cos17°.
b)
c) tan 885° = tan(180.4 + 165°) = tan165° = tan(180° ‒ 15°) = ‒tan15°.
d)
Câu 6:
23/07/2024Chứng minh các đẳng thức sau:
a)
b)
 Xem đáp án
Xem đáp án
a) sin605° = sin(3.180° + 65°) = ‒sin65°.
sin1645° = sin(9.180° + 25°) = ‒sin25° = ‒sin(90° ‒ 65°) = ‒cos65°.
cot25° = cot(90° ‒ 65°) = tan65°.
sin2605° + sin21645° + cot225°
= (‒sin65°)2 + (‒cos65°)2 + (tan65°)2
= 1 + tan265°
b) sin530° = sin(3.180° ‒ 10°) = sin10°.
sin640° = sin(4.180° ‒ 80°) = ‒sin80° = ‒sin(90° ‒ 10°) = ‒cos10°.
Câu 8:
14/07/2024Tính giá trị của các biểu thức sau:
a) sin 17°sin197° + sin73°cos163°;
b)
 Xem đáp án
Xem đáp án
a) Ta có:
sin197° = sin(180° + 17°) = ‒sin17°.
sin73° = sin(90° ‒ 17°) = cos17°.
cos163° = cos(180° ‒ 17°) = ‒cos17°.
Suy ra:
sin 17°sin197° + sin73°cos163°
= sin 17°.(‒sin17°) + cos17°.(‒cos17°)
= ‒(sin217° + cos217°) = ‒1.
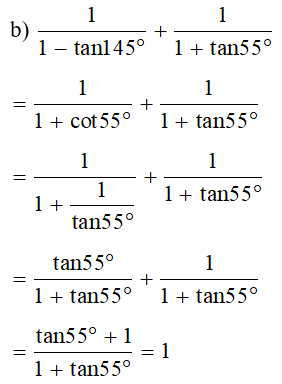
Câu 9:
19/07/2024a) Cho tanα + cotα = 2. Tính giá trị của biểu thức tan3α +cot3α.
b) Cho Tính giá trị của sinαcosα.
c) Cho Tính giá tị của biểu thức sin3α + cos3α.
 Xem đáp án
Xem đáp án
a) tan3α + cot3α = (tanα + cotα)3 ‒ 3tanαcotα(tanα + cotα)
= (tanα + cotα)3 ‒ 3 (tanα + cotα) (*)
Thay tanα + cotα = 2 vào biểu thức (*) ta có: 23 ‒ 3.2 = 2.
b) (sinα + cosα)2 = sin2α + cos2α + 2 sinαcosα = 1 + 2 sinαcosα.
Do đó .
c) sin3α + cos3α
= (sinα + cosα)(sin2α ‒ sinαcosα + cos2α)
= (sinα + cosα)(1 ‒ sinαcosα)
Mà , nên
.
Câu 10:
20/10/2024Cho tanx = 2. Tính giá trị của các biểu thức sau:
a)
b) Xem đáp án
Xem đáp án
*Phương pháp giải
Biến đổi biểu thức đã cho về tỉ số lượng giác cho trước. (sử dụng công thức )
*Lời giải
Vì tanx xác định nên cosx ≠ 0. Chia tử và mẫu của phân thức cho luỹ thừa thích hợp của cosx để biểu diễn biểu thức theo tanx.
a) .
b)
Xem thêm các bài viết liên quan hay, chi tiết:
Tổng hợp bảng giá trị lượng giác
Trắc nghiệm Giá trị lượng giác của một góc bất kì từ 0 độ đến 180 độ có đáp án
Câu 11:
22/07/2024Độ dài của ngày từ lúc Mặt Trời mọc đến lúc Mặt Trời mọc ở một thành phố X trong ngày thứ t của năm được tính xấp xỉ bởi công thức:
với t ∈ ℤ và 1 ≤ t ≤ 365.
Thành phố X vào ngày 31 tháng 1 có bao nhiêu giờ có Mặt Trời chiếu sáng? Làm tròn kết quả đến hàng phần mười.
 Xem đáp án
Xem đáp án
Thay t = 31 vào công thức trên ta có:
(giờ)
Vậy thành phố X vào ngày 31 tháng 1 có 9,01 giờ có Mặt Trời chiếu sáng.